
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод эквивалентного генератора
|
|
 |
В практических расчётах часто нет необходимости знать режимы работы всех элементов сложной цепи, но ставится задача исследовать режимы работы одной определённой ветви.
При расчёте сложной электрической цепи приходится выполнять значительную вычислительную работу даже в том случае, когда требуется определить ток в одной ветви. Объём этой работы в несколько раз увеличивается, если необходимо установить изменение тока, напряжения, мощности при изменении сопротивления данной ветви, так как вычисления нужно производить несколько раз, задаваясь различными значениями сопротивления.
В любой электрической схеме можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от структуры и сложности, условно изобразить прямоугольником, который представляет собой так называемый двухполюсник.
Таким образом, двухполюсник - это обобщённое название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Если в двухполюснике есть источник Э.Д.С. или тока, то такой двухполюсник называют активным. Если в двухполюснике нет источника Э.Д.С. или тока, то его называют пассивным.
При решении задачи методом эквивалентного генератора (активного двухполюсника) необходимо:
 |
1. Мысленно заключить всю схему, содержащую Э.Д.С. и сопротивления, в прямоугольник, выделив из нее ветвь аb, в которой требуется найти ток (рис 2.13).
1. Найти напряжение на зажимах разомкнутой ветви ab (в режиме холостого хода).
Напряжение холостого хода Uо (эквивалентное Э.Д.С. Еэ) для рассматриваемой цепи можно найти так: 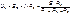 .
.
Сопротивление R4 в расчёт не вошло, так как при разомкнутой ветви ab ток по нему не протекает.
3. Найти эквивалентное сопротивление. При этом источники Э.Д.С. закорачиваются, а ветви, содержащие источники тока, размыкаются. Двухполюсник становится пассивным.
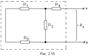
Для данной схемы
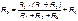 .
.
4. Вычислить значение тока. Для данной схемы имеем: 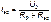 .
.
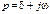 , осуществляемой в соответствии с функциональным преобразованием Лапласа. При этом каждой временной функции
, осуществляемой в соответствии с функциональным преобразованием Лапласа. При этом каждой временной функции 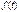 , называемой оригиналом (прообразом), ставится в соответствие функция
, называемой оригиналом (прообразом), ставится в соответствие функция 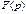 , именуемая изображением (образом). Эта операция записывается f (t)· = · F (p). В результате такой замены система дифференциальных уравнений для оригиналов преобразуется в систему алгебраических уравнений для их изображений. В результате решения этой системы определяют изображение
, именуемая изображением (образом). Эта операция записывается f (t)· = · F (p). В результате такой замены система дифференциальных уравнений для оригиналов преобразуется в систему алгебраических уравнений для их изображений. В результате решения этой системы определяют изображение  искомой величины, а на заключительном этапе переходят к физически понятной функции – оригиналу
искомой величины, а на заключительном этапе переходят к физически понятной функции – оригиналу 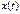 .
Подобный прием применялся при анализе стационарного решения цепей символическим методом. Однако в то время, как символический метод можно применять лишь к гармоническим функциям, операторный метод обладает значительно большей общностью и применим к широкому классу функций.
9. Исследование переходных процессов при помощи интеграла Дюамеля.
Последовательность расчета с использованием интеграла Дюамеля.
.
Подобный прием применялся при анализе стационарного решения цепей символическим методом. Однако в то время, как символический метод можно применять лишь к гармоническим функциям, операторный метод обладает значительно большей общностью и применим к широкому классу функций.
9. Исследование переходных процессов при помощи интеграла Дюамеля.
Последовательность расчета с использованием интеграла Дюамеля.  Определение функции
Определение функции 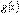 (или
(или 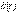 ) для исследуемой цепи.
Запись выражения
) для исследуемой цепи.
Запись выражения  (или
(или 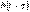 ) путем формальной замены t на
) путем формальной замены t на 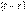 .
Определение производной
.
Определение производной 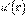 .
Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета:
.
Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: 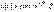 ,
, 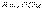 ,
, 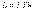 .
Переходная проводимость
.
Переходная проводимость
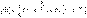 .
.
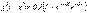 .
.
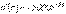 .
.

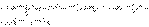 Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
10. Нелинейные электрические цепи постоянного тока.
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.
Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.
Нелинейные элементы можно разделить надвух– и многополюсные.Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи.
18.Мгновенная и средняя мощности. Активная, реактивная и полная мощности. Измерение мощности ваттметром
Если имеются законы изменения тока и напряжения
Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
10. Нелинейные электрические цепи постоянного тока.
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.
Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.
Нелинейные элементы можно разделить надвух– и многополюсные.Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи.
18.Мгновенная и средняя мощности. Активная, реактивная и полная мощности. Измерение мощности ваттметром
Если имеются законы изменения тока и напряжения
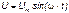 ,
, 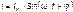 ,
то их произведение
,
то их произведение
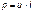 Мгновенная мощность
Мгновенная мощность
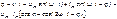 График этой функции - результат графического умножения графиков тока и напряжения.
Под активной мощностью Р понимают среднее значение мгновенной мощности за период Т:
График этой функции - результат графического умножения графиков тока и напряжения.
Под активной мощностью Р понимают среднее значение мгновенной мощности за период Т:
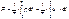 .
Учитывая соотношения можно записать
.
Учитывая соотношения можно записать

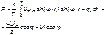 (3.36)
Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R. Действительно, произведение
(3.36)
Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R. Действительно, произведение 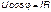 . Следовательно:
. Следовательно:
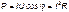 . (3.37)
Единица активной мощности - 1Вт (Ватт).
Под реактивной мощностью Q принимают произведение напряжения на участке цепи на ток, протекающий по этому участку, и на синус угла φ между напряжением и током.
. (3.37)
Единица активной мощности - 1Вт (Ватт).
Под реактивной мощностью Q принимают произведение напряжения на участке цепи на ток, протекающий по этому участку, и на синус угла φ между напряжением и током.
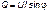 . (3.38)
Единица реактивной мощности – вольт-ампер реактивный (ВАр).
Величина, объединяющая активные реактивные мощности, называется полной мощностью.
. (3.38)
Единица реактивной мощности – вольт-ампер реактивный (ВАр).
Величина, объединяющая активные реактивные мощности, называется полной мощностью.
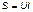 . (3.39)
Единица полной мощности - вольт-ампер (ВА).
Для того, чтобы вычислить полную мощность нужно комплекс напряжения умножить на сопряженный комплекс тока:
. (3.39)
Единица полной мощности - вольт-ампер (ВА).
Для того, чтобы вычислить полную мощность нужно комплекс напряжения умножить на сопряженный комплекс тока:
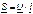 . (3.40)
Можно расписать
. (3.40)
Можно расписать
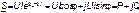 . (3.41)
Таким образом, активная мощность Р есть действительная часть (Re), а реактивная Q - мнимая часть (Im) произведения
. (3.41)
Таким образом, активная мощность Р есть действительная часть (Re), а реактивная Q - мнимая часть (Im) произведения 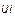
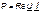 , (3.42)
, (3.42)
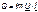 . (3.43)
22.Трёхфазные цепи.Общее..
Объединение в одной линии электропередачи нескольких цепей переменного тока с независимыми источниками электроэнергии называется многофазной системой.
Наибольшее распространение получила трёхфазная система, которая была изобретена и разработана выдающимся русским инженером М. О. Доливо-Добровольским в 1889-1891гг.
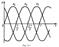
Трёхфазной симметричной системой Э.Д.С. называется совокупность трёх Э.Д.С. одинаковой частоты и амплитуды, сдвинутых друг относительно друга по фазе на 1200 . Эти три Э.Д.С. можно изобразить на временной (рис.5.1) и векторной (рис. 5.2.) диаграммах.
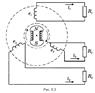
Трёхфазные симметричные системы Э.Д.С. получаются с помощью трёхфазного генератора, в котором имеются три самостоятельные обмотки, расположенные на статоре, и сдвинутые относительно друг друга в пространстве на 1200. В центре статора вращается магнит (рис. 5.3). Форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по синусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут индуцироватьсяЭ.Д.С.равной амплитуды и частоты, отличающиеся друг от друга на 1200.
. (3.43)
22.Трёхфазные цепи.Общее..
Объединение в одной линии электропередачи нескольких цепей переменного тока с независимыми источниками электроэнергии называется многофазной системой.
Наибольшее распространение получила трёхфазная система, которая была изобретена и разработана выдающимся русским инженером М. О. Доливо-Добровольским в 1889-1891гг.
Трёхфазной симметричной системой Э.Д.С. называется совокупность трёх Э.Д.С. одинаковой частоты и амплитуды, сдвинутых друг относительно друга по фазе на 1200 . Эти три Э.Д.С. можно изобразить на временной (рис.5.1) и векторной (рис. 5.2.) диаграммах.
Трёхфазные симметричные системы Э.Д.С. получаются с помощью трёхфазного генератора, в котором имеются три самостоятельные обмотки, расположенные на статоре, и сдвинутые относительно друг друга в пространстве на 1200. В центре статора вращается магнит (рис. 5.3). Форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по синусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут индуцироватьсяЭ.Д.С.равной амплитуды и частоты, отличающиеся друг от друга на 1200.
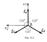
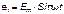 ; (5.1)
; (5.1)
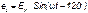 ; (5.2)
; (5.2)
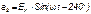 . (5.3)
Комплексы действующих значений этих Э.Д.С.:
. (5.3)
Комплексы действующих значений этих Э.Д.С.:
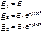
 Следующий порядок чередования Э.Д.С.
Следующий порядок чередования Э.Д.С.  называется прямой последовательностью фаз, а чередование
называется прямой последовательностью фаз, а чередование 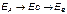 называется обратной последовательностью фаз.
В дальнейшем при рассмотрении трёхфазных систем принимается прямая последовательность фаз, которая считается нормальной.
26.Эквивалентные схемы четырёхполюсника
Для пассивных четырёхполюсников чаще выбирают Т- или П- образную схему замещения, состоящую из трёх независимых элементов. Иногда применяют мостовую (Х образную) схему замещения.
называется обратной последовательностью фаз.
В дальнейшем при рассмотрении трёхфазных систем принимается прямая последовательность фаз, которая считается нормальной.
26.Эквивалентные схемы четырёхполюсника
Для пассивных четырёхполюсников чаще выбирают Т- или П- образную схему замещения, состоящую из трёх независимых элементов. Иногда применяют мостовую (Х образную) схему замещения.
 |
Т - и П – образные схемы замещения представлены на (рис. 7.2 и 7.3) соответственно.
Значения трёх сопротивлений этих схем определяют с учетом того, что схема замещения должна обладать теми же коэффициентами A, B, C, D, что и заданный четырехполюсник.
Т- образная схема (схема звезды)
Для этой схемы справедливы следующие соотношения:
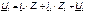
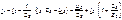
Подставив значения 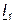 в первое уравнение получим:
в первое уравнение получим:
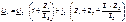 ; (7.9)
; (7.9)
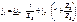 , (7.10)
, (7.10)
Сравнивая полученные уравнения 7.9 и 7.10 с системой уравнений формы А 7.1 и 7.2 записываем значения искомых величин:
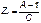
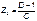

П – образная схема (схема треугольника)

Аналогичные приёмы для П- схемы дают:
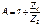
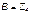
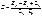
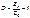
Тогда можно записать искомые значения сопротивлений:
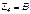 ;
; 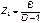
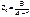
Если четырёхполюсник симметричный, то в Т – схеме 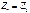 , а в П- схеме
, а в П- схеме