Смешанное соединение

Рисунок 1.20 - Смешанное соединение сопротивлений

Смешанным соединением сопротивлений называется такое соединение, при котором действуют одновременно и параллельное и последовательное соединение.

Согласно схеме имеем

Рисунок 1.21 - Промежуточное преобразование смешанного соединения

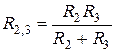и далее,

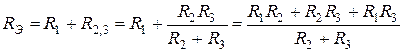. (1.22)

Отсюда найдем токи:

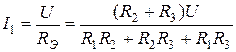; (1.23)

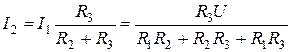; (1.24)

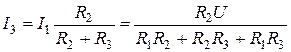. (1.25)

В результате преобразования удалось решить разветвленную цепь простыми средствами, в нашем случае, даже без составления уравнений.

Следует иметь в виду, что при преобразовании схемы, состоящей только из сопротивлений (ветви не имеют источников энергии), мощность в эквивалентной схеме равна мощности в заданной неразветвленной цепи.

1.6.5 Преобразование «треугольника сопротивлений» в «звезду сопротивлений»

Впервые данное преобразование осуществлено итальянским ученым Кеннели.

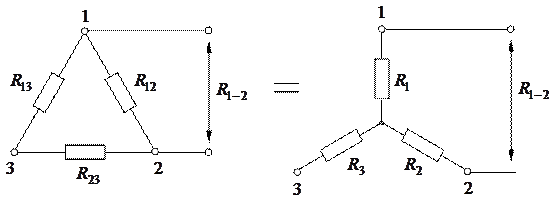Составляем расчетную схему.

Рисунок 1.22 - Преобразование «D» сопротивлений в «U»

Для треугольника сопротивлений дано: .

Найти: .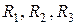

Уравнения перехода от треугольника к звезде сопротивлений запишутся:

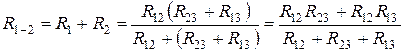; (1.26)

; (1.27)

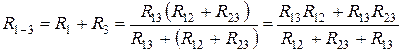. (1.28)

Решим полученную систему относительно неизвестных 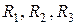. Для этого сложим (1.26) и (1.28) и вычтем (1.27).

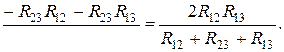(1.29)

Откуда получаем

,

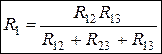аналогично имеем:

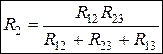; (1.30)

.

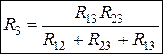Выражения (1.30) позволяет определить сопротивления лучей звезды по заданным сопротивлениям сторон треугольника.

В частом случае, при симметричном треугольнике, когда все сопротивления сторон треугольника одинаковы, , сопротивления лучей звезды также будут одинаковы, .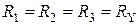

Согласно выражений (1.30), получаем:

;

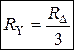. (1.31)