Обратная матрица

Определение 1. Пусть задана квадратная матрица 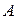. Матрица называется обратной матрицей к матрице 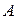, если выполнено соотношени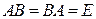е , где 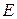- единичная матрица той же размерности.

Обратную матрицу мы будем обозначать символом .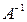

Теорема 1. Для квадратной матрицы 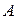обратная матрица существует тогда и только тогда, когда определитель матрицы 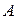не равен 0.

Доказательство. Необходимость. Пусть обратная матрица существует. Так как определитель произведения матриц равен произведению определителей, то справедливо соотношение 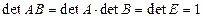. В этом равенстве ни один из множителей не может быть равным 0. Поэтому 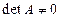. Необходимость условия теоремы доказана.

Достаточность. Пусть определитель матрицы 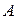не равен 0. Докажем, что обратная матрица существует. Доказательство будет носить конструктивный характер. Мы просто в явном виде построим эту матрицу. Одновременно будет показан способ построения обратной матрицы.

Шаг № 1. Вычислим 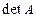и убедимся в том, что он не равен 0.

Шаг № 2. Составим матрицу из алгебраических дополнений к элементам матрицы .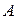

Шаг № 3. Транспонируем матрицу, построенную в п. 2.

Шаг № 4. Поделим каждый элемент матрицы, построенной в п. 3, на .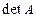

Докажем, что полученная при этом матрица и будет искомой обратной матрицей матрицы 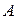. Пусть заданная матрица имеет вид , тогда после шага 2 мы получим матрицу 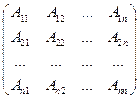, которая после шага 3 превратится в матрицу 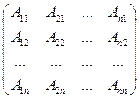. Найдем произведение этой матрицы и заданной матрицы 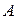в том и другом порядке. Итак, запишем

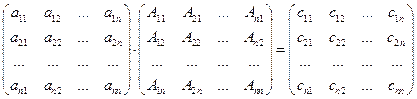и вычислим все :

, …

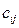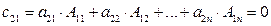Первое из этих равенств справедливо, потому что получается сумма попарных произведений элементов первой строки матрицы 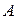на их алгебраические дополнения, т. е. определитель матрицы 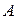. Второй элемент равен 0, т.к. он равен сумме попарных произведений элементов второй строки матрицы 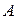на алгебраические дополнения к элементам ее первой строки, т. е. это разложение по первой строке определителя, у которого первая и вторая строки равны. В итоге все элементы , а остальные элементы , если 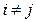. Аналогичный результат получится при рассмотрении произведения 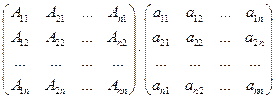, только здесь будет разложения по столбцам матрицы 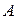. Теорема доказана, т.к. если в этих произведениях все элементы 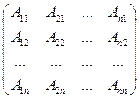поделить на 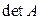, то результатом произведения матриц будет единичная матрица.

Пример 1. Найдем обратную матрицу для матрицы .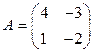

Шаг № 1. Вычислим .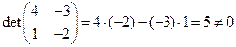

Шаг № 2. Составим матрицу 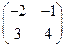из алгебраических дополнений к элементам матрицы .

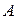Шаг № 3. Транспонируя эту матрицу, получим .

Шаг № 4. Поделим каждый элемент этой матрицы на 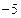и найдем обратную матрицу .

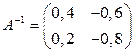Проверим, что полученная матрица 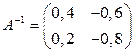и будет искомой обратной матрицей. Вычислим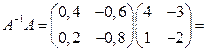 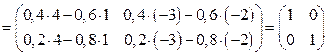. Аналогично .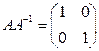