СЛАУ, матричный вид СЛАУ

В различных приложениях получение важных результатов связано с необходимостью решения СЛАУ – системы линейных алгебраических уравнений. Запишем общий вид СЛАУ

(1)

Здесь неизвестные 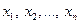можно воспринимать как вектор неизвестных , коэффициенты при неизвестных 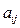, , 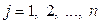- как матрицу неизвестных 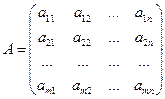, правые части 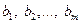можно воспринимать как вектор неизвестных 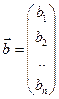. При таких обозначениях уравнение (1) запишется в виде 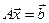(1’).

Пример 2. Запишите систему 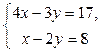в матричном виде и найдите ее решение.

Запишем систему в матричном виде 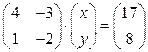. Матрицу 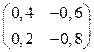умножим на равные вектора – матрицы размерност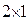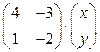и : и . Тем самым мы получим верное равенство 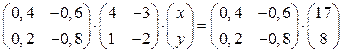. В примере 1 мы показали, что матрицы 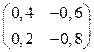и 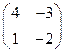являются взаимно обратными и их произведение равно единичной матрице 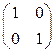. Следовательно, 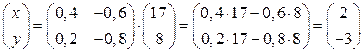и , .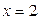

Этот, матичный, и другие методы решения СЛАУ мы изучим на следующей лекции.