
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристики различных типов лопастных колес
|
|
| Типы лопастных колес | nS, мин-1 | D2/ D1 |
| 1. Центробежные тихоходные | 40 – 80 | 2, 5 |
| 2. Центробежные нормальные | 80 – 150 | 2, 0 |
| 3. Центробежные быстроходные | 150 – 300 | 1, 4 – 1, 8 |
| 4. Диагональные | 300 – 600 | 1, 1 – 1, 2 |
| 5. Осевые | 600 – 1800 | 0, 6 – 0, 8 |
Теоретический напор, создаваемый колесом центробежного насоса, равен разности напоров на выходе и входе в него
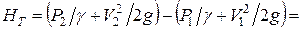
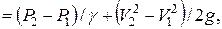 (7. 28)
(7. 28)
где Р 1 и Р 2 – давления жидкости, Па, на входе и выходе из колеса;
V 1 и V 2 – абсолютные скорости, м/с, на входе в колесо и выходе из колеса;
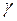 – удельный вес жидкости, Н/м3 (для нефтепродукта плотностью
– удельный вес жидкости, Н/м3 (для нефтепродукта плотностью
850 кг/м3, 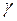 = 8330 Н/м3).
= 8330 Н/м3).
В выражение 7.28 входят значения давления Р1 и Р2, их можно заменить значениями скоростей, используя уравнение Бернулли для течения жидкости в межлопаточных каналах
P 1 / 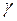 +W
+W 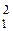 / 2 g = P 2 /
/ 2 g = P 2 / 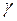 + W
+ W 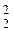 / 2 g – Hц, (7.29)
/ 2 g – Hц, (7.29)
где W 1 и W 2 – относительные скорости (касательные к поверхности лопатки) на входе и выходе из колеса;
Нц = (U 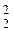 – U
– U 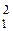 )/ 2 g – напор, возникающий от работы центробежных сил, здесь U 1 и U 2 – окружные скорости на входе и выходе из рабочего колеса.
)/ 2 g – напор, возникающий от работы центробежных сил, здесь U 1 и U 2 – окружные скорости на входе и выходе из рабочего колеса.
На рис. 7.7 показаны планы скоростей на входе (точка 1) и выходе из колеса (точка 2) центробежного насоса.
После подстановки выражения 7.29 в выражение 7.28, преобразуя и сокращая, получим уравнение Леонардо Эйлера (1707 – 1783 гг., член Петербургской академии наук) для колес с радиальным входом жидкости
HТ = U 2∙ V2 cos 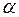 2 /g, (7.30)
2 /g, (7.30)
где 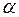 2 – угол между векторами окружной U 2 и абсолютной V 2 скоростями на выходе из колеса;
2 – угол между векторами окружной U 2 и абсолютной V 2 скоростями на выходе из колеса;
g – ускорение свободного падения, 9, 8 м/с2.
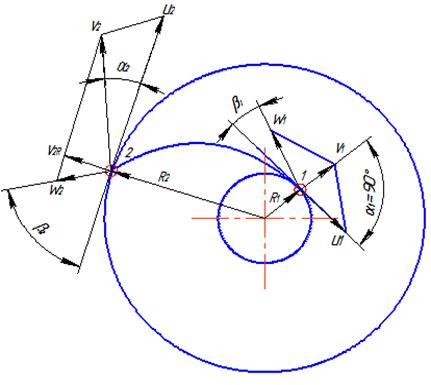
Рис. 7.7. Планы скоростей на входе и выходе из колеса
Для колеса с радиальными лопатками V 2 cos 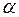 2 = U 2 и уравнение 7.30 принимает более простой вид
2 = U 2 и уравнение 7.30 принимает более простой вид
HТ = U 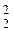 / g. (7.31)
/ g. (7.31)
Значение окружной скорости на выходе из колеса определяют из выражения
U 2 = 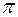 ∙ n ∙ D2 / 60, (7.32)
∙ n ∙ D2 / 60, (7.32)
где n – частота вращения вала насоса, мин-1 (750, 1500, 3000).
При известных значениях n и D 2 можно определить теоретический напор HТ, создаваемый колесом.
В процессе вращения колеса под действием центробежных сил частицы жидкости перемещаются от центра к периферии. Напор создается рабочим колесом в результате:
1) работы центробежных сил (U 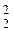 – U
– U 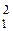 )/ 2 g – статический напор;
)/ 2 g – статический напор;
2) прироста кинетической энергии абсолютного движения (V 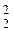 – V
– V 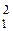 ) /2 g – динамический (скоростной) напор;
) /2 g – динамический (скоростной) напор;
3) преобразования величины относительной скорости (W21 – W22)/2g – статический напор.
На рис. 7.8 показаны формы лопаток центробежных машин (направление вращения по часовой стрелке).
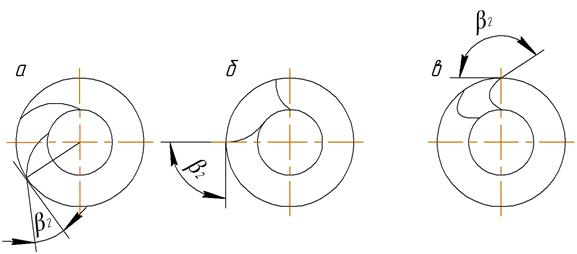
Рис. 7.8. Формы лопаток: а – загнутые назад; б – с радиальным (по радиусу) выходом;
в – загнутые вперёд
В зависимости от формы лопаток в общем напоре, создаваемом колесом, статический и динамический напор распределяются следующим образом:
1) лопатки радиальные – примерно 50 % статический напор и 50 % динамический (применяют в центробежных насосах, дымососах);
2) лопатки загнутые назад – преобладает статический напор (применяют в центробежных насосах);
3) лопатки загнутые вперед – преобладает динамический напор или энергия скорости (применяют в вентиляторах).
От выбранного количества лопаток и их толщины зависит проходное сечение колеса. Уменьшение проходного сечения на выходе из колеса учитывается коэффициентом стеснения К 2, который равен 0, 85 – 0, 95 и определяется выражением
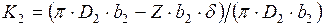 , (7.33)
, (7.33)
где b 2 – ширина проходной части колеса на выходе, b 2= (0, 05 – 0, 1) D 2;
D 2– диаметр колеса на выходе; Z – количество лопаток (5 – 13); 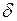 – толщина лопаток (
– толщина лопаток (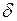 = 0, 1 – 0, 3) b 2.
= 0, 1 – 0, 3) b 2.
Колесо насоса при степени быстроходности 100 – 150 имеет максимальный коэффициент полезного действия при числе лопаток, равных 7 – 11.
Совершенство центробежного насоса оценивают коэффициентом полезного действия (КПД).
Объемный КПД (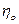 ) учитывает перетекание жидкости из полости нагнетания в полость всасывания через зазоры между корпусом насоса и колесом, равен 0, 85 – 0, 95.
) учитывает перетекание жидкости из полости нагнетания в полость всасывания через зазоры между корпусом насоса и колесом, равен 0, 85 – 0, 95.
Гидравлический КПД (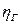 ) учитывает совершенство проточной части колеса (потери на трение, образование вихрей) и равен 0, 85 – 0, 95.
) учитывает совершенство проточной части колеса (потери на трение, образование вихрей) и равен 0, 85 – 0, 95.
Механический КПД ( ) учитывает потери на трение в подшипниках и уплотнениях, равен 0, 95 – 0, 98.
) учитывает потери на трение в подшипниках и уплотнениях, равен 0, 95 – 0, 98.
Общий КПД насоса равен 0, 70 – 0, 90 и определяется из выражения
 (7.34)
(7.34)