
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доверительный интервал и надежность
|
|
Среднее арифметическое аср результатов проведенной серии измерений производится со случайной ошибкой. Оно не равно истинному значению измеряемой величины. Поэтому, давая окончательный результат проведенных измерений, необходимо указывать не только значения аср , но и еще доверительный интервал и надежность.
Доверительным интерваломназывается интервал (аср - Dа, аср + Dа), в который попадает истинное значение х искомой величины с заданной вероятностью(надежностью).
Надежностью (Р) результатов серии измерений называется вероятность того, что истинное значение измеряемой величины попадает в данный интервал(надежность выражается в долях единицы или в процентах). Чем больше доверительный интервал, тем больше надежность того, что искомая величина попадает в этот интервал.
Рассмотрим функцию распределения вероятности отклонений отдельных результатов измерений от среднего арифметического (5). График такой функции в зависимости от Dаi / σ имеет вид, изображенный на рис. 2.
Рис. 2. Функция распределения вероятности отклонения случайных ошибок отдельных результатов измерений.
В теории вероятности доказывается, что
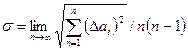 , (6)
, (6)
где n – число проведенных измерений.
Вычислив корень квадратный из дисперсии (6) и задав доверительный интервал ± Dа, мы можем отложить на оси абсцисс (рис. 2) значения аргумента функции распределения, соответствующие границам доверительного интервала
± Dа / σ (на рис. 2. Dа / σ = 1).
Тогда надежность имеет смысл площади под кривой функции распределения, ограниченной вдоль оси абсцисс границами доверительного интервала. Таким образом, по заданному доверительному интервалу можно найти надежность. Очевидно, полная площадь под кривой функции распределения равна единице, так как она соответствует вероятности того, что истинное значение измеряемой величины лежит в доверительном интервале (аср - ¥; аср + ¥), а это достоверно.
Пользуясь изложенным методом, можно, наоборот, по заданной надежности найти величину доверительного интервала.
5. Средняя квадратичная ошибка. Коэффициент Стьюдента [1]
Величина, стоящая под знаком предела в формуле (6)
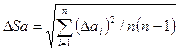 , (7)
, (7)
называется средней квадратичной ошибкой. Она зависит от числа nпроделанных измерений и равна корню из дисперсии только в пределе n ® ¥. Практически можно считать, что при n > 30
DSa 
Если по условиям опыта, например в условиях учебной лаборатории, нельзя провести большое число измерений данной величины, то пользоваться формулой (8) нельзя, а, следовательно, и нельзя определить доверительный интервал, так как величина σ нам неизвестна.
Для оценки доверительного интервала при небольшом количсстве измерений вводится коэффициент
t = D a / Sa, 
который зависит как от выбора надежности Р, так и от числа проделанных измерений n. Этот коэффициент получил название коэффициента Стьюдента.
Отсюда D a = t · DSa. (9)
Обычно коэффициент Стьюдента находится по таблицам (см. табл. 1 прилож.).