Методы моделирования событий

ЛАБОРАТОРНАЯ РАБОТА №6

МОДЕЛИРОВАНИЕ ПРОСТЫХ, ПОЛНОЙ ГРУППЫ И СЛОЖНЫХ СОБЫТИЙ

Цель – изучение методов моделирования случайных событий, влияющих на поведение сложных систем управления.

Методы моделирования событий

Моделирование простого события A с вероятностью P(A) заключается в сравнении равномерно распределенного в пределах (0, 1) случайного числа 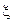с численным значением вероятности события A. Если число 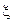не превысило вероятность P(A), т.е. 0< 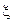£ P(A), то произошло событие A.

Моделирование полной группы событий 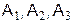с вероятностью P(A₁), P(A₂), P(A₃), причем 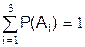, заключается в сравнении числа 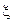с отрезками, длины которых образованы последовательным суммированием вероятностей P(A_i), где 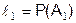, , 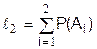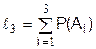. Поэтому, если число 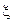не превысило суммы вероятностей P(A₁) и P(A₂), то произошло событие A­₂.

Моделирование сложных независимых событий A и B с вероятностью P(A) и P(B) заключается в определении одного исхода из полной группы совместных испытаний: 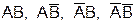. Моделирование независимых событий можно выполнить двумя способами - по схеме простых и полной группы событий.

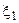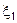
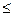Способ моделирования по схеме простых событий заключается в последовательном сравнении чисел с вероятностями событий P(A) и P(B). В случае, если не превысило вероятности P(A), а - превысило P(B), т.е. (0< P(A), P(B)< 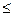1), то результатом моделирования является исход .

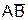При использовании схемы полной группы событий число 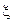сравнивается с отрезками, длины которых образованы последовательным суммированием вероятностей: 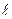₁=P₁, 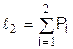,..., . 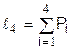Сумма вероятностей P_i представляет собой полную группу совместных испытаний, т.е.

.

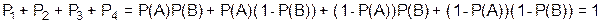Если число 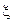превысило вероятность P₁ =P(A)P(B) и является меньшим или равным P₁+P₂=P(A)P(B)+P(A)(1-P(B)), то результатом моделирования сложных независимых событий A и B является исход .

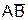Моделирование сложных зависимых событий A и B с вероятностями P(A), P(B) и условной вероятности события B при условии, что событие A произошло - P(B/A), заключается в определении одного исхода из полной группы совместных испытаний .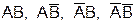

Моделирование сложных зависимых событий A и B по схеме простых событий заключается в последовательном сравнении чисел 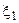и с вероятностями событий P(A) и P(B/A). Поэтому, если 0< 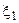£ P(A) (A - произошло) и P(B/A)< £ 1 (B - не произошло), то результатом испытания является исход 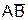. В случае, когда событие A не произошло, вычисляется условная вероятность P(B/ 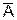) по формуле:

,

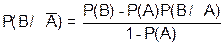с которой сравнивается число 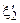. В результате моделирования, если P(A)< 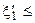1 и 0<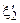 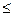P(B/ 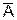), то исходом испытания является 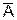B.

Моделирование сложных зависимых событий A и B по схеме полной группы событий заключается в:

- описании возможных исходов зависимых событий ;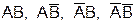

- составлении полной группы событий:

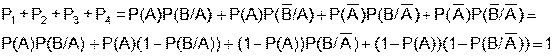
- сравнении числа 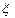с отрезками, длины которых образованы последовательным суммированием вероятностей:

l₁= P₁, .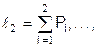

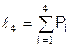Если 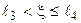, то результатом моделирования сложных зависимых событий является исход .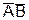