
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет центрально-сжатых элементов
|
|
В условиях центрального сжатия находятся такие элементы деревянных конструкций, как колонны и стойки, подкосы, ряд элементов ферм и др.
Короткие стержни, у которых длина незначительно превышает размеры поперечного сечения, рассчитывают на прочность по выражению
 , (2.6)
, (2.6)
где N – расчетное усилие;
F нт – площадь сечения рассматриваемого элемента;
R с – расчетное сопротивление древесины сжатию вдоль волокон.
Однако, чаще всего, сжатые элементы по длине l существенно превышают наименьший размер поперечного сечения b (l ≥ 7b), в этом случае сжатый элемент рассчитывается на устойчивости по формуле
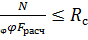 , (2.7)
, (2.7)
где F расч – расчетная площадь поперечного сечения элемента;
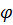 - коэффициент продольного изгиба (коэффициент снижения основного расчетного сопротивления R c).
- коэффициент продольного изгиба (коэффициент снижения основного расчетного сопротивления R c).
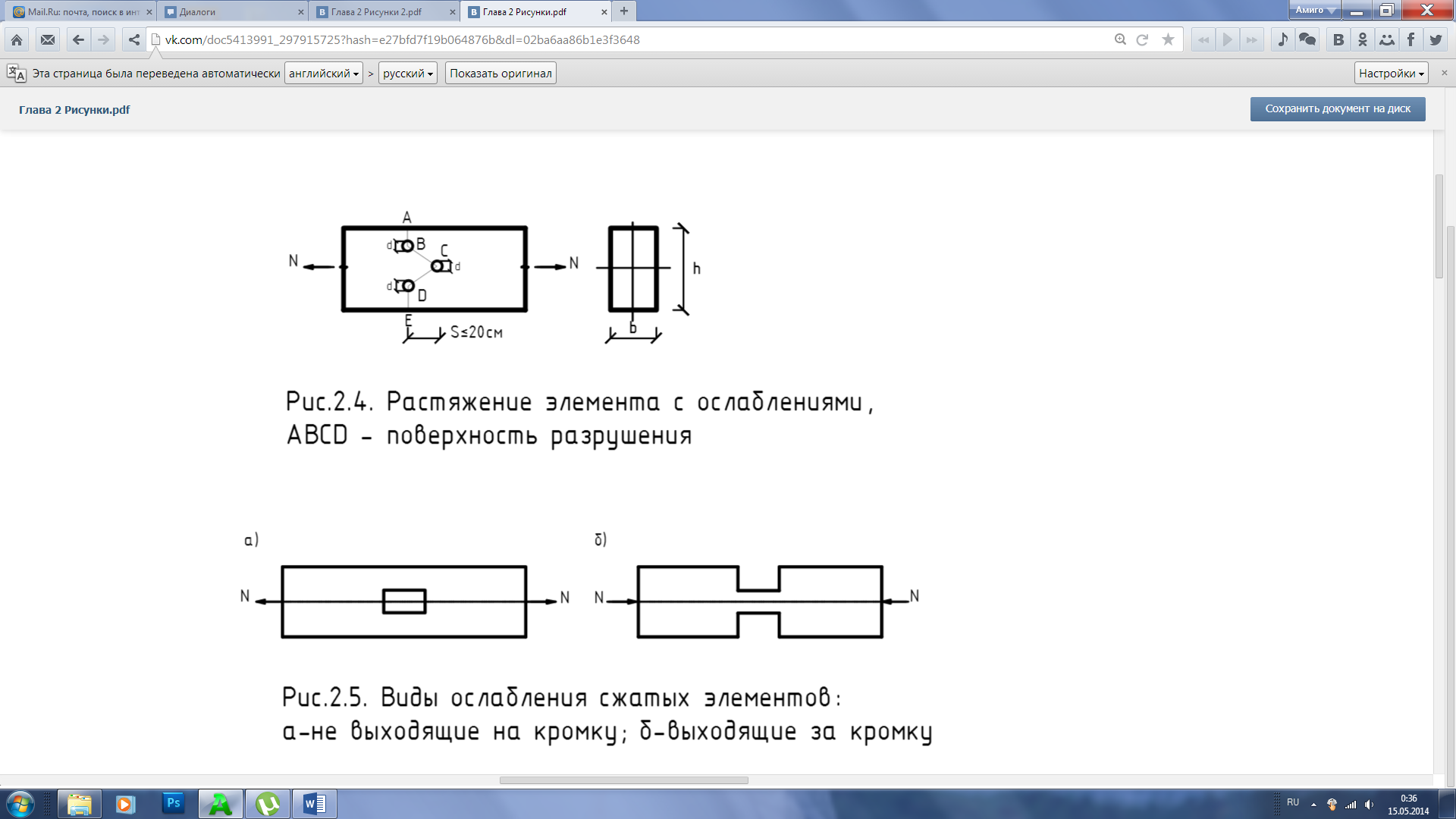
Рис.2.5 Виды ослабления сжатых элементов:
а-не выходящие на кромку, б-выходящие на кромку
Величина F расч принимается, равной (рис.2.5.):
- при отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки, при условии, что площадь ослабления не выше 25% F бр
 (2.8)
(2.8)
где F бр – площадь сечения брутто;
- при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25% F бр
 , (2.9)
, (2.9)
Коэффициент продольного изгиба зависит от гибкости элемента λ х относительно оси наименьшей жесткости сечения стержня
 , (2.10)
, (2.10)
где l0=μ l - расчетная (приведенная) длина стержня, зависящая от условий закрепления стержня (рис.2.6);
l – длина стойки;
μ – коэффициент приведения длины стержня, зависящий от условий закреплений стойкии от способа приложения нагрузки;
rх – радиус инерции сечения относительно оси наименьшей жесткости (относительно оси x момент инерции минимален).

Рис.2.6 Расчетные длины деревянных центрально-сжатых элементов
Радиус инерции сечения равен
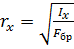 , (2.11)
, (2.11)
где I x – момент инерции сечения (для круглого сечения с диаметром d радиус инерции равен r x = d /4, для прямоугольного сечения - rx =0, 289 b, b – наименьший размер сечения).
Коэффициент продольного изгиба деревянных сжатых стержней определяется по формулам:
при гибкости элемента λ х> 70
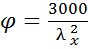 , (2.12)
, (2.12)
при гибкости элемента λ х≤ 70
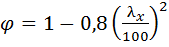 . (2.13)
. (2.13)
Максимальная гибкость сжатых деревянных элементов не должна превышать следующих предельных значений:
сжатые пояса, опоры, раскосы и стойки ферм, колонны……………λ max≤ 120;
прочие сжатые элементы………………………………………………λ max≤ 150;
сжатые элементы связей……………………………………………… λ max≤ 200.