Оптимизация реактивной мощности в системе

В качестве источников реактивной мощности, которые могут использоваться для оптимизации режима энергосистемы, будем рассматривать синхронные генераторы электростанций и синхронные компенсаторы системных подстанций.

Генерация реактивной мощности не связана непосредственно с расходом топлива, но влияет на него через изменение потерь в сети. Таким образом, в качестве критерия принимается минимум потерь с учетом баланса реактивной мощности:

;

,

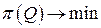где q(Q) – потери реактивной мощности в сети,

Q_HS – общая нагрузка, определяется с учетом зарядных мощностей.

Составим функцию Лагранжа:

,

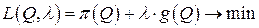условие минимума которой по всем источникам

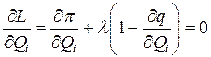
позволяет получить следующее равенство

.

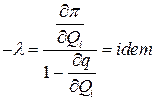Смысл этого условия можно определить, если рассмотреть конечные приращения

,

т.е. приращения потерь в сети по отношению к изменению реактивной мощности всех источников с учетом потерь на 1 МВАр должны быть равны.

Если в качестве БУ принять источник Q_n, то для него и всех остальных должно выполняться условие 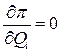. В этом случае оптимальные реактивные мощности можно найти по общей формуле потерь, полученной ранее для активных мощностей и аналогичной ей

.

Откуда

и решение в матричной форме

.

Здесь вектор C_Q определяется по заданным узловым реактивным нагрузкам с использованием коэффициентов токораспределения в R-схеме.

Оптимизация реактивных мощностей должна проводится с учетом ограничений по напряжению.