
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
А, в, с
|
|

 front rear
front rear
Элементті ө шіру
 |
front rear
В элементін ө шіру
front rear
 DEF элементін қ осу
DEF элементін қ осу
front rear
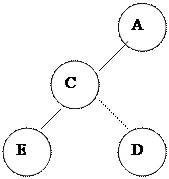
Осындай модельмен жү ргізіледі. Бұ л модель тиімді емес. Мысалғ а, шіретте 1000 элемент болсын. Егер басынан 1 элемент ө шірілсе (кетсе) онда 999 элемент солғ а қ арай жылжуы керек. Мұ ндай жағ дайда сақ иналық шірет тиімді. Сақ иналық шіреттің элементтері логикалық тү рде шең берге ұ йымдастырылады (сақ иналық). Front айнымалысы шіреттегі бір элементтің орыны болып табылады жә не ол ө шірулерді орындағ ан сайын шең бер бойымен оң ғ а қ арай жылжиды. Массив негізінде:

 2. rear 1. rear front
2. rear 1. rear front
front
A-ны ө шіру
 rear
rear
front front
rear
D-ны қ осу Е-ні қ осу
Шіреттерді кө рсеткіштер кө мегімен жү зеге асыруда шірет ө лшемі кіруге болатын бос жадының кө лемімен шектеледі. Оны графикпен келесі тү рде беруге болады:

|
|
|
|
|
|
|
|
 | |||||||||
 |  |  | |||||||
 |
Null
Шірет объектісімен жү ргізілетін операциялар
1. Шіретке элементті қ осу
2. Шіреттен элементті алып тастау (ө шірілген элементтің мә нін беру)
3. Бірінші элементтің мә нін беру.
4. Шіретті тазалау
5. Шірет элементінің санын беру.
Шіреттер қ олданылады:
1. Компьютерлік модельдеуде (банктегі клиент шіретін модельдеу)
2. Кө п адамдар қ олданылатын операциялық жү йелерде.
3. Мә ліметтерді сұ рыптауда
Приоритеттер шіреті
Приоритеттер шіреті дегеніміз – бұ л тзімнен жоғ ары приоритетті элемент ө шірілетін шіреттің модификацияланғ ан версиясы.
Шіреттегі элементтер кілт жә не мә н жұ бы ретінде қ арастырылады. Мұ нда кілт приоритеттің дең гейін кө рсетеді. Приоритет қ андай да бір сыртқ ы критерий бойынша бағ аланады. Приоритет шіретіндегі элементті ө шіруде приоритеті бірдей элемент қ атар келсе, алдымен бірінші тү скен элемент ө шіріледі. 0 приоритеті жоғ ары болып саналады. Келесі элементтер тізімін жә не приоритетін қ арастырсақ сақ талу реті
| Элемент 1 | Элемент 2 | Элемент 3 | Элемент 4 | Элемент5 |
Ең алдымен 2 ө шіріледі.
2, 1, 5, 4, 3
орындалу реті
| Элемент 1 | Элемент 2 | Элемент 3 | Элемент 4 | Элемент5 |
2, 1, 5, 4, 3
| Элемент 1 | Элемент 2 | Элемент 3 | Элемент 4 | Элемент5 |
Пиоритеттер шіретін ә рбір шіреттер приоритеті ү шін қ олданылатын бірнеше шіреттер тү рінде беруге болады. Приоритеттер шіретін процестеп, тізімге жазатын жә не одан кейін приоритеттер реті бойынша орындайтын операциялық жү йеде қ олдануғ а болады.
Дә ріс 10.
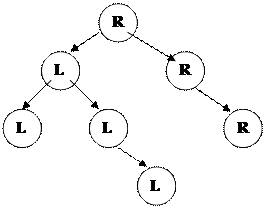
Ағ аштар. Тармақ тар.
Мақ саты: Ағ аштар немесе тармақ тар ұ ғ ымын енгізу, негізгі тү сініктерін беру, екілік тармақ қ ұ рылымымен таныстыру.
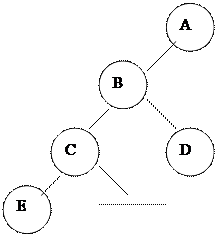
Тармақ дегеніміз – иеархиялық қ ұ рылым қ ұ ратын элементтер мен қ атынастардың жиынтығ ы.
Тармаќтыњ элементтері т‰йін деп аталады. Аѓаш тєрізді ќ±рылым т‰пкі деп аталатын алѓашќы бір т‰йіннен басталатын кµптеген т‰йіндер жиынтыѓын ќ±райды.
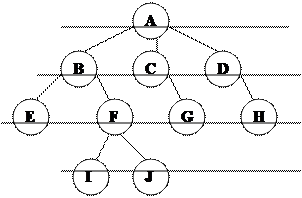 |
0-дењгей 1-дењгей 2-дењгей 3-дењгей
М±нда аѓаштыњ т‰бірі дегеніміз – ары ќарай т‰бірі болмайтын тµбесі, яѓни м±ндаѓы А. Єрбір тармаќтыњ бір ѓана т‰бірі болады. Тармаќтыњ ењ тµменгі т‰йіндері E, F, G, H жапыраќ деп аталады. Егер тармаќтыњ элементі жапыраќ болмаса, онда оны тармаќтыњ ішкі т‰йіні немесе тµбесі деп аталады. Бос тармаќ дегеніміз – ешќандай тµбесі жоќ тармаќты атаймыз. Балалыќ тµбесі деп – тармаќта орналасќан µзініњ ата-аналыќ тµбесінен тµмен ќарай т±рѓан жєне онымен тікелей байланысќан тµбені атаймыз. Мысалѓа, егер i тµбесі F тµбесіне ќатысты балалыќ тµбесі болса, онда F тµбесі I тµбесіне ќатысты ата-аналыќ тµбе деп аталады.
Балалыќ т‰йіндер жєне олардыњ балалыќ т‰йіндері ±рпаќ деп аталады. Мысалѓа, E, F жєне I, J B – т‰йінініњ ±рпаќтары.
Тектері б±л т‰йінніњ ата-аналары немесе ата-єжелері.
Тармаќтыњ єрбір т‰йіні осы т‰йіннен жєне барлыќ ±рпаќтарынан т±ратын б±таќтыњ т‰бірі болып табылады. Мысалы, В тµбесі E, F, I, J дењгейініњ т‰йіні. Мысалѓа, F т‰йіні F, I, J т‰йіндерінен т±ратын б±таќтыњ т‰бірі болып табылады. G т‰йіні ±рпаќсыз б±таќтыњ т‰йіні. А т‰йіні µзі тармаќ болып табылатын б±таќтыњ т‰бірі.
Кез келген т‰йіннен т‰йіннен бастап оныњ ±рпаќтарына ќарай ж‰ру белгілі бір жол бойымен ж‰зеге асады. Мысалѓа, А т‰бірінен бастап F т‰йініне дейінгі жол A, B, F тµбелерінен µтеді. Кез келген т‰йіннен оныњ ±рпаќтарына баратын жол жалѓыз ѓана болады. Т‰йінніњ дењгейі дегеніміз – ол т‰бірден осы осы т‰йінге дейінгі жолдыњ ±зындыѓы. Мысалѓа, А т‰бірініњ дењгейі 0-ѓа тењ. Т‰бірдіњ єрбір баласыныњ дењгейі 1-ге тењ. Мысалѓа F т‰йіні 2 дењгейдегі ±зындыѓы 2-ге тењ т‰йін болып табылады.
Тармаќтыњ терењдігі дегеніміз – оныњ кез келген т‰йінініњ максимальды дењгейі немесе тармаќтыњ терењдігі дегеніміз ол т‰бірден бастап т‰йінге дейінгі ењ ±заќ жолдыњ ±зындыѓы.
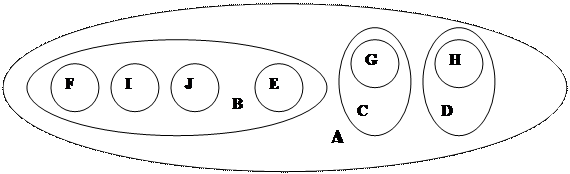
Тармақ тә різді қ ұ рылымды беру ә дістері
Тармақ тарды берудің 4 тү рлі ә дісі бар:
2. графтар
3. кірістірілген жақ шалар
4. кірістірілген жиындар
5. кесінді тізбектер.
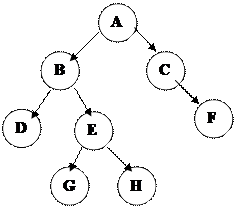
1. Графтар. Бә рі А тү йінінен тарайды

2. Кірістірілген жақ шалар:
(A(B(E, F(I, J)), C(G), D(H)))
3. Кірістірілген жиындар.
 |
4. Кесінді тізбек.
A B E I
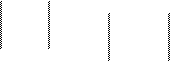 F J
F J
C G
D H
Кө бінесе тармақ тарды бейнелеу ү шін графтар қ олданылады.
Дә ріс 11.
Екілік бинарлық тармақ тар. Екілік тармақ тардың қ ұ рылымы.
Мақ саты: Екілік бинарлық тармақ тар ұ ғ ымын қ алыптастыру. Екілік тармақ тардың қ ұ рылымы беру.
Программалауда екілік тармақ тар кең қ олданылады. Екілік тармақ тар келесі қ асиеттерге ие:
1. екілік тармақ та ә рбір тө бенің екіден артық балалық тү йіні болмайды.
2. кез келген тө бенің балалық тө белері оң жақ балалық тө бе жә не сол жақ балалық тө бе болып бө лінеді. (Бұ л тармақ тардың графтық берілуіне қ атысты айтылады. Кез келген тармақ тарды оғ ан сә йкес екілік тармақ ретінде беруге болады)
Екілік тармақ рекурсивті қ ұ рылымды болды. Себебі ә рбір тү йіні ө зінің астындағ ы бұ тақ тың тамыры немесе тү бірі болып табылады. Оны ө здері де (бұ тақ тың) сол жақ жә не оң жақ бұ тақ тардың тү бірлері болып табылатын балалары бар. Сондық тан тармақ тарды ө ң деу процедуоамы кө бінесе рекурсивті болып табылады. Екілік тармақ дегеніміз – ү ш қ иылыспайтын ішкі жиындарғ а бө лінетін тү йіндер жиыны. Мұ нда {R} – тү бірлі тү йін, {L1, L2, …, Ln} – R сол жақ бұ тақ, {R1, R2, …, Rn} – R оң жақ бұ тақ. Яғ ни оны былай бейнелеуге болады.
 |
Оң жақ бұ тақ
Сол жақ бұ тақ
Екілік тармақ кез келген n дең гейде бірден бастап 2n тү йіндерге дейін болуы мү мкін. Тармақ тардың тығ ыздығ ы дегеніміз – тармақ тың тү йіндерінің оның терең дігіне қ атысты саны.
Мә ліметтер қ ұ рылмы ретінде жоғ ары тығ ыздық тағ ы тармақ тар маң ызды болып табылады. Яғ ни, тығ ыз тармақ мә ліметтің кө п қ ұ рылымын сақ тай алады жә не элементтерге кіруді тиімді жү зеге асыра алады.
Туындағ ан тармақ тар, аяқ талғ ан тармақ тар тығ ыздық шеткі шаралары немесе ө лшемдері болып табылады. n терең діктегі аяқ талғ ан 2-к тармақ дегеніміз – 0-дан бастап n-1 –ге дейінгі ә рбір дең гейі тү йіндерінің толық жиыны бар жә не n дең гейіндегі барлық жапырақ тары сол жағ ынан орналасқ ан екілік тармақ тарды айтамыз. Толық тармақ дегеніміз – бұ л n дең гейді 2n тү йіндерде тұ ратын аяқ талғ ан бинарлық тармақ.
Туындалғ ан тармақ Аяқ талғ ан тармақ
(4-дең гей) (3-дең гей)
 | |||
 | |||
Толық тармақ
(2-дең гей)
 |
Тармақ тың терең дігі дегеніміз – оның тү бірінен ең шеткі тү йініне дейінгі ең ұ зын жолдың ұ зындығ ы болады. Мысалғ а, n тү йіні бар туындалғ ан тармақ ү шін ең ұ зақ жол ұ зындығ ы n-1-ге тең болады. Сонда 5 тү йіні бар тармақ тың максимальды терең дігі 4-ке тең болады. N тү йіні бар аяқ талғ ан тармақ ү шін log2n-ң бү тін бө лігіне тең болады. Мысалы, егер тармақ тың 10000 элементі болса, n=10000, онда терең дігі - int(log21000)= int(13, 28)=13.
Екілік тармақ тың қ ұ рылымы.
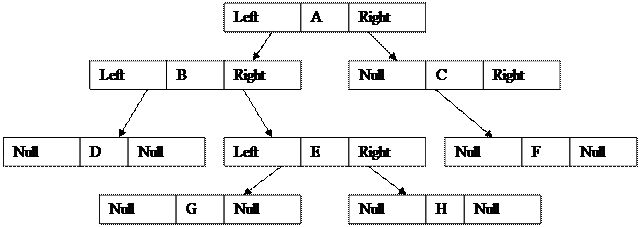
Екілік тармақ ты компьютер жадысына берудің екі тү рлі жолы бар.
1. Кә дімгі массивті пайдалана отырып тізбектеп беру
2. Динамикалық қ ұ рылым ретінде беру.
Массивті пайдалана отырып тізбектеп беруде екілік тармақ бір ө лшемдік массивке қ апталады. Мұ ндай беруде тек бір ғ ана TREE сызық ты массиві қ олданылады. Тармақ тың тү бірі массивтің бірінші элементі TREE[0] –де орналасады. Келесі екі балалық тө белері кө ршілес элементтерде орналасады. Т.с.с.
Егер n тү йіні массивтің TREE[k] элементін алатын болса, онда оның сол жақ тағ ы балалық тү йіні TREE[2K+1], ал оң жақ тағ ы блалық тү йіні - TREE[2K+2].
Кемшіліктері:
1. Тармақ тың ө лшемі массив ө лшемімен шектелетін болады.
2. Тығ ыздығ ы кө п емес тармақ ты сақ тау ү шін кө п бө лігі пайдасыз қ алатын ү лкен массив керек болады.
Екілік тармақ тарды жү зеге асыру ү шін кө бінесе мә ліметтердің динамикалық қ ұ рылымдары пайдаланылады. Тармақ тың ә рбір тү йінінде мә ліметтер ө рісі жә не кө рсеткіштері бар 2 ө ріс болады.
Кө рсеткіштер ө рістері – сол жақ кө сеткіш жә не оң жақ кө рсеткіш деп аталады. Себебі, олар сә йкес сол жә не оң тармақ қ а кө рсетеді.
Жапырақ тық тү йін – сол жә не оң жақ тү йін кө рсетуде Null болады.
 | |||
 |
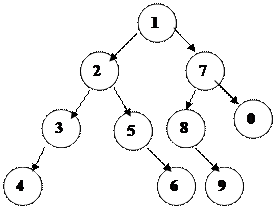
Айталық, бізге n тү йіні бар минимальды биіктікпен тармақ салу керек. Ол ү шін барлық дең гейлердегі тү йіндердің ең жоғ арғ ы мү мкін санын, ең тө менгісін санамағ анда білуіміз керек. Идеал балансталғ ан тармақ - бұ л ең тө менгісін санамағ андағ ы барлық дең гейлердегі тү йіннің ең жоғ арғ ы мү мкін саны бар тармақ. Идеалды балансталғ ан тармақ та ә рбір тү йін ү шін тү йіндер саны оң жә не сол жақ бұ тақ та айырмашылығ ы бірге ғ ана тең болады. N тү йіні берілгенде идеалды балансталғ ан тармақ ты жасаудың алгоритмі:
1. тү бір ретінде бір тү йінді алу.
2. nl=n/2 тү йіні бар сол жақ бұ тақ салу (осы алгоритм кө мегімен)
3. nr=n-nl-1 оң жақ бұ тақ салу (алгоритм кө мегімен)
Мысалы, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 сандар тізбегі ү шін идеалды балансталғ ан тармақ келесі тү рде болады:
 |
Ө рнектердің екілік тармақ тары
Екілік тармақ тар типіндегі қ ұ рылыстар матрицалық ө рнектерді беруде кө п қ олданылады. Мысалғ а, 2+3 ө рнегін мына тү рде жазуғ а болады (екілік тармақ ретінде):
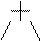 |
2 3
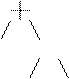 7+(6*4) ө рнегін келесі тү рде:
7+(6*4) ө рнегін келесі тү рде:
7 *
6 4
Тармақ тардың мұ ндай типтері ө рнектер тармақ тары деп аталады. Мұ ндай тармақ тардың ә рқ айсысы қ ө андай да бір ө рнектерді сипаттайды. Тек қ ана екілік амалдарды сипаттайтын екілік тармақ тар ө рнектердің екілік тармақ тары деп аталады. (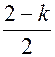 амалдар дегеніміз – бұ л тек қ ана операндасы бар амалдар).
амалдар дегеніміз – бұ л тек қ ана операндасы бар амалдар).
Ө рнектің екілік тармақ тары келесі қ асиеттерге ие болады:
1. Ә рбір жапырақ тық тө бе бір ғ ана операндқ а ие болады (операнд - сандар), ал жапырақ емс тө бе – амалғ а ие болады.
2. Ә рбір бұ тақ қ андай да бір туындыны қ ұ райды.
3. Сол жақ немесе оң жақ бұ тақ тың тү біріне сә йкес амалды орындамас бұ рын есептеліп шық қ ан болуы керек.
Ө рнектер тармақ тары ө рнектер симантикасы анализіне арналғ ан компелятор мен импетаторларда кө п қ олданылады. Ал оның жалпыланғ ан ұ ғ ымы программалар синтаксисі анализі ү шін компиляторларда қ олданылады.
Дә ріс 12.
Екілік іздеу тармақ тары
Мақ саты: Екілік іздеу тармақ тары ұ ғ ымы. Екілік тармаќтармен жү ргізілетін амалдар. Байланғ ан сызық тық тізімдер тү сініктерін енгізу.
Екілік іздеу тармақ тары программалауда кең таралғ ан. Екілік іздеу тармақ тарының ә рбір тө бесінің мә ні:
1. Оның сол жағ ындағ ы бұ тақ тө бесінің кез келген мә нінен ү лкен немесе тең.
2. Оның оң жақ бұ тағ ының тө бесінің кез келгенінің мә нінен кіші.
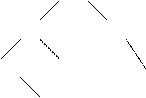
 5 7
5 7
2 8 5 8
0 7 0 6
9 9
6 2
Программада екілік іздеу тармағ ының таралуы бұ л тармақ тарда іздеу ә дістерінің тиімділігінің нә тижесі болып табылады.
Сызық тық қ ұ рылғ ылар ү шін тізбектеліп іздеу алгоритмінің кү рделілігі – О(n) –ғ а тең. Мұ ндағ ы n-қ ұ рылым элементтер саны. Ал аяқ талатын бинарлық тармақ ү шін кү рделілігі – О(log2n)-ғ а тең.
Мысалғ а: 10000 элементтен тұ ратын тізімде тізбектеп іздеуде салыстырудың максимальды саны 10000-ғ а тең болады. Ал аяқ талғ ан тармақ та іздеу 14 салыстырудан аспас еді.
Екілік іздеу тармағ ына элементті осу алгоритмі (тармақ ты қ арау ү немі тү бірден басталады):
1. тармақ қ а қ осылатын мә н ағ ымдағ ы тү йін мә ніне салыстырылады.
2. Егер тармақ қ а қ осылтын мә н ағ ымдағ ы тү йін мә нінен кіші болса, онда келесілер тексеріледі:
а) егер ағ ымдағ ы тү йінде ұ рпақ тар жоқ болса, онда жаң ағ ы мә ні бар тү йінді сол жақ ұ рпақ ретінде бекітеміз.
б) ә йтпесе, (егер ұ рпақ болса) тармақ тың сол жақ бұ тағ ы арқ ылы бір дең гейге тө мендетеміз.
3. Егер тармақ қ а қ осылатын мә н ағ ымдағ ы тү йін мә нінен ү лкен немесе тең болса, келесілер тексеріледі:
а) егер оң жақ тағ ы ағ ымдағ ы тү йінде ұ рпақ тар жоқ болса, онда мә ні бар тү йінді оң жақ ұ рпқ ретінде бекітеміз.
б) ә йтпесе, оң жақ бұ тақ бойымен бір дең гейге тө мендетеміз.
Екілік тармаќтармен ж‰ргізілетін амалдар
1. Тармаќты толыѓымен ќарап µту алгоритмі
Тармаќтыњ тµбелерін с±рыптау алгоритмі – тармаќты толыѓымен ќарап µту алгоритмі деп аталады. М±ндай алгоритмдер т‰йінде ‰ш т‰рлі єрекет жасайды: т‰йінге кіреді, сол жаќ б±таќпен рекурсивті т‰рде тµмендейді, рекурсивті т‰рде оњ жаќ б±таќпен тµмендейді.
Тармаќты ќарап шыѓудыњ 3 т‰рлі негізгі єдісі бар:
1. Тура єдіс;
2. Симметриялы єдіс;
3. Кері єдіс;
Тармаќты толыѓымен ќарап шыѓу алгоритмі олардыњ тү йініндегі µздерініњ єрекеттерімен байланысты реттерімен ажыратылады.
1. Тура єдіс (жоѓарыдан тµмен ќарай):
- т‰йінге кіру;
- сол жаќ б±таќтан µту;
- оњ жаќ б±таќтан µту;
 (1) 7
(1) 7
5 8
0 6 9
Екілік тармаќ берілген. Б±л тармаќтаѓы т‰йінге кіру реті келесідей болады:
7 5 0 2 6 8 9
2. Симметриялыќ єдіс (солдан оњѓа ќарай):
- сол жаќ б±таќтан ж‰ріп µту;
- т‰йінге кіру;
- оњ жаќ б±таќтан ж‰ріп µту;
Берілген (1) тармаќ ‰шін симметриялыќ ќарап шыѓу келесі т‰рде болады:
0 2 5 6 7 8 9
Екілік тармаќты симметриялыќ ќарап шыѓу єдісі элементтерді µсу ретімен орналастырды. Осылайша, с±рыптаудыњ таѓы бір алгоритмін ±сынуѓа болады:
А) массив негізінде с±рыптау;
В) тармаќты симметриялыќ ќарап шыѓу єдісі ж‰зеге асады;
М±ндаѓы ењ жаќсы жаѓдайда алгоритмніњ тиімділігі O(n log2n) болады.
3. Тармаќты кері ќарай ќарап шыѓу єдісі (тµменнен жоѓарыѓа ќарай):
- сол жаќ тармаќтан ж‰ріп µту;
- оњ жаќ тармаќтан ж‰ріп µту;
- т‰йінге кіру;
Осы єдіс ‰шін тармаќты ж‰ріп µтудіњ жолы:
2 0 6 5 9 8 7
¤рнектіњ екілік тармаќтарын ќарап µтуде жоѓарыда берілген ‰ш єдіспен мынаны аламыз:
1. Ќарап шыѓудыњ тура єдісі. ¤рнектерді жазудыњ префиксті форматына (жоѓарыдан тµменге ќарай) сєйкес келеді.
2. Ќарап шыѓудыњ симметриялыќ єдісі µрнектерді жазудыњ инфиксті форматина сєйкес келеді.
3. ќарап шыѓудыњ кері єдісі µрнектерді жазудыњ постфиксті форматына сєйкес келеді.
2. Екілік іздеу тармаѓынан элементті алып тастау.
Тармаќтан элементті алып тастау алгоритмі тармаќтаѓы осы элементтіњ орналасќан орнына тєуелді болады жєне келесі тµрт жаѓдайды ќамтиды:
1. Мєні х-ке тењ болатын элемент жоќ.
2. Мєні х-ке тењ болатын элемент терминальды т‰йін болып табылады.
3. Мєні х-ке тењ болатын элемент бір ѓана ±рпаќты болады.
4. Мєні х-ке тењ болатын элемент екі ±рпаќты болады.
Бір ѓана ±рпаѓы болатын элементті алып тастауда ешќандай к‰рделілік жоќ. М±ндай єрекеттер сызыќтыќ тізімдегі элементті алып тастауѓа ±ќсас болады.
 | |||
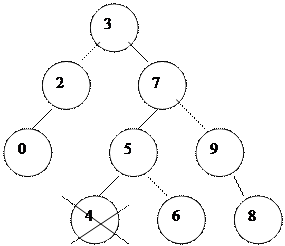 | |||
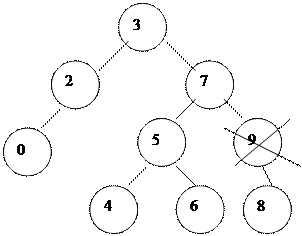
Егер элемент екі ±рпаќты болса, онда екі баѓытта бір ѓана сілтемемен кµрсетуге келмейді. Б±л жаѓдайда µшірілетін элементті ауыстыруѓа тура келеді. Ауыстыратын элемент ‰шін оныњ сол жаќтаѓы ењ оњ жаќќы элемент, ал оњ жаќтаѓы ењ сол жаќќы элемент тањдап алынады (6 жєне 8 µшірілетін элементке мєндері жаѓынан жаќын элементтер).
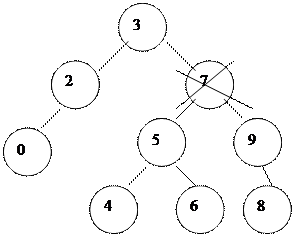 |
Элементі µшіру алгоритмі. Алгоритм жоѓалѓанда ќарастырылатын 4 жаѓдайды ќамтиды:
1-жаѓдай: µшірілетін т‰йін табылѓан жоќ. Яѓни µшірук алгоритмі µз ж±мысын тоќтатады.
2-жаѓдай: т‰йінніњ ±рпаќтары жоќ. Яѓни жапыраќ болып табылады. Б±л жаѓдайда ата-аналыќ т‰йінді оныњ б±таѓы бос болатындай етіп жањарту керек.
3-жаѓдай:
1. Т‰йінніњ сол жаќ ±рпаѓы бар, оњ жаќ ±рпаѓы жоќ. Яѓни сол жаќ б±таќты оныњ ата-анасына жалѓастыру керек.
2. Т‰йінніњ оњ жаќ ±рпаѓы бар, сол жаќ ±рпаѓы жоќ. Яѓни т‰йінніњ оњ жаќ б±таѓын оныњ ата-анасына жалѓастыру керек.
4-жаѓдай: екі ±рпаѓы бар т‰йінді алып тастау немесе µшіру. М±нда µшірілетін т‰йінді ауыстыру ќажет. Ауыстыру ‰шін сол жаќ б±таѓы ењ оњ жаќтаѓы т‰йінді тањдаймыз.
Келесілерді аныќтаймыз:
D – µшірілетін т‰йін
P – µшірілетін элементтіњ ата-анасы
R – ауыстыратын т‰йін
PR – R т‰йінніњ ата-анасы.
1. D т‰йінініњ сол жаќ б±таѓына кµшеміз. Себебі, R ауыстыратын т‰йін µшірілетін D т‰йінінен кіші болады.
2. R ауыстыратын т‰йін D т‰йінініњ сол жаќ б±таѓындаѓы максимальды т‰йін болып табылады. Оњ жаќ б±таќ бойынша тµмен жылжып, P ауыстыратын т‰йінді іздейміз. Жылжу барысында RR ата-аналыќ т‰йінді баќылап отырамыз. М±нда екі м‰мкін жаѓдай бар:
1. Оњ жаќ б±таќ бос. R ауыстытылатын т‰йін µшірілетін т‰йінніњ сол жаќ баласы болып табылады. Ал PR сєйкесінше D т‰йініне кµрсетіледі. М±ндай жаѓдайда келесі єрекеттерді орындаймыз:
А) D т‰йінініњ оњ жаќ б±таѓын R т‰йініне ќосамыз.
Б) ¤шірілетін т‰йінніњ P ата-анасын R т‰йініне ќосамыз.
 |  | ||
P P
D R
R PR=D
Оњ жаќ б±таќ оњ жаќ б±таќ
2. Оњ жаќ б±таќ бос емес. М±ндай жаѓдайда ауыстыратын т‰йін жапыраќтыќ т‰йін болады немесе тек ќана сол жаќ б±таѓы бар т‰йін болады. Келесі єрекеттерді орындаймыз:
А) R т‰йінін тармаќтан бµліп аламыз.
Б) R т‰йінініњ ±рпаќтарын оныњ ата-аналыќ РR т‰йініне жалѓаймыз. (R-діњ сол жаќ б±таѓы РR-ѓа оњ жаќ б±таќ болып жалѓанады).
С) ¤шірілетін D т‰йіні R т‰йінімен ауыстырылады. Яѓни D т‰йінініњ ±рпаќтары R т‰йінініњ ±рпаќтары болып жалѓанады, ал R т‰йіні ата-аналыќ P т‰йініне жалѓанады.
Дә ріс 13.
Массивтермен берілген бинарлыќ тармаќтар
Мақ саты: Массивтермен берілетін бинарлық тармақ тар ұ ғ ымын енгізу. Турнирлік сұ рыптау, пирамидалар тү сініктерін енгізу.
Массивтермен берілген бинарлыќ тармаќтар екіге бµлінеді:
1. Турнирлік с±рыптау.
2. Пирамидалар.
Егер бинарлыќ мєліметтер элементтерде саќталса, онда мєліметтерге тура кіруді ж‰зеге асыруѓа болады. Массивтіњ 0-элементі б±л тармаќтыњ тамыры немесе т‰бірі. n элемент массиві ‰шін ai т‰йінніњ ±рпаќтарын келесі формуламен есептеуге болады. Сол жаќтаѓы индекс - 2i+1, ал оњ жаќтаѓы индекс - 2i+2-ге тењ, ал ата-анасыныњ индексін - (i-1)/2 формуласымен аныќтаймыз. Тармаќталѓан массивті пайдалану беруді аяќтаѓалѓан бинарлыќ тармаќ ‰шін ќолдану ќолайлы. Біраќ тыѓыздыѓы аз болатын тармаќты саќтаѓанда массивте пайдаланылмайтын элементтер болады да массивпен ж±мыс істеуде бірќатар ќиындыќтар туѓызуы м‰мкін. Мысалы:
A[]=(5, 1, 3, 9, 6, 2, 4, 7, 0, 8)
Турнирлік с±рыптау
Бинарлыќ тармаќтар шешімдер ќабылдау термаќтары ретінде кµп ќолданылады. Мысалы, спорттыќ турнирді алайыќ. М±нда єрбір ішкі т‰йін екі ойыншыныњ кездеріндегі жењімпазѓа сєйкес келеді.
Турнирлыќ m, n элементтен m массивті с±рыптауѓа ќолданылуы м‰мкін. Турнирлыќ с±рыптауды келесі мысалда ќарастырайыќ:
A[8]=(35, 25, 50, 20, 15, 45, 10, 40)
Осы массивті µсу ретімен с±рыптау ќажет.
1. Массив элементтері бинарлыќ тармаќ к дењгейінде болады. М±ндаѓы: 2k> =n n – массив элементтер саны. Б±л жаѓдайда 23=8, яѓни k=3 болады.
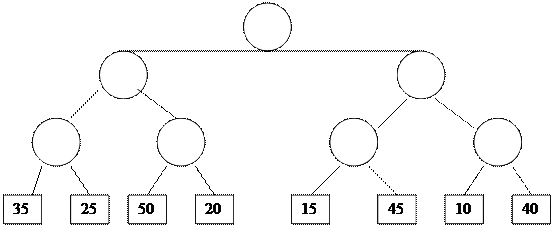 |
2. Ата-аналыќ т‰йінге ж±птарѓа элементтердіњ кішісі орналасады, ењ соњѓы салыстыру нєтижесінде массивтіњ ењ кіші элементі 0-дењгейіне (тамырына) т‰седі.
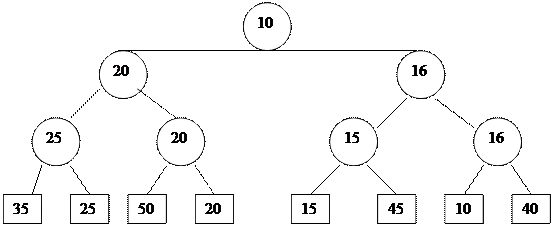
3.
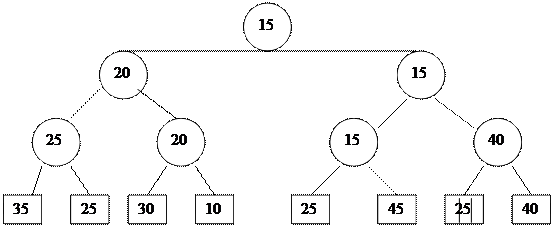 Бір элемент алынып тасталады.
Бір элемент алынып тасталады.
4. 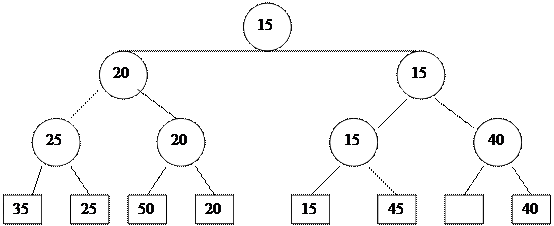
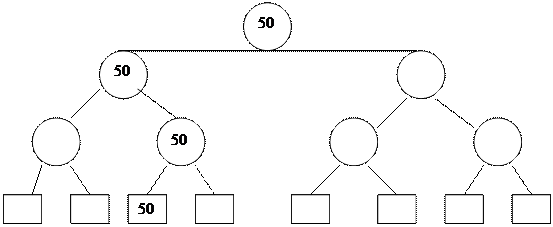 5.
5.
Осы процесс барлыќ жапыраќтары алынып тасталѓанша ж‰ргізіліп ж‰ре береді. Ењ соњѓы т‰йін (ењ ‰лкен элемент) барлыѓын ‰нсіз келісім бойынша шыѓады.
Дә ріс 14.
Пирамидалар
Мақ саты: Пирамидалар, негізгі тү сініктерін беру. Пирамидаларда тү рлендірулер жү ргізу, амалдар қ олдану.
Пирамида дегеніміз – дењгейлер бойынша т‰йінтік реттілігі бар бинарлыќ тармаќ. Пирамидаларды максимальды пирамидалар жєне минимальды пирамидалар деп бµледі.
Максимальды пирамида – ата-аналыќ т‰йін µзініњ балаларыныњ єрќайсыснан ‰лкен немесе тењ болады. Т‰бірде ењ ‰лкен элемент жатады.
Минимальды пирамида – ата-аналыќ т‰йін µзініњ балаларыныњ єрќайсысынан кіші немесе тењ болады. Ал т‰бірде ењ кіші элемент жатады.
Мысалѓа, минимальды пирамидаѓа:
 |
 Мысалѓа, максимальды пирамидаѓа:
Мысалѓа, максимальды пирамидаѓа:
Пирамидалар клиентке минимальды элементке тура кіру жаѓдайында ќолданылады. Пирамида тізім болып табылады. Онда мєліметтер бинарлыќ тармаќ т‰рінде саќталады. Пирамидаларды µњдейтін барлыќ алгоритмдер µздері тармаќты жањартып, пирамидалыќ реттеуді ж‰зеге асырып отырулады ќажет.
Массивті пирамидаѓа т‰рлендіру
Пирамиданыњ соњѓы элементініњ индексі n-1-ге тењ. Оныњ ата-анасыныњ индексі n-2-ге тењ. Жєне ол пирамидалардыњ соњѓы жапыраќтыќ емес т‰йін болып табылады. Осы индекс массивті т‰рлендіру ‰шін бастапќы индекс болып табылады. Мынадай б‰тін санды массив берілсін:
А(10)=(9, 12, 17, 30, 50, 20, 60, 65, 4, 19)
Оны пирамида т‰рінде былай жазамыз:
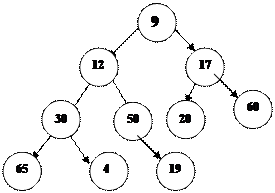 |
М±ндай жапыраќтардыњ индекстары 5, 6, 7, 8, 9 болады. Ата-анасының индекстары – 0, 1, 2, 3, 4.
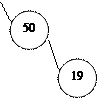 |
- қ арастырамыз.
А(4)=50 ата-анасы ө зінің А(9)=19 деген ұ рпағ ынн ү лкен болып табылады. Сондық тан А(9) бен А(4) орындарын ауыстырамыз:
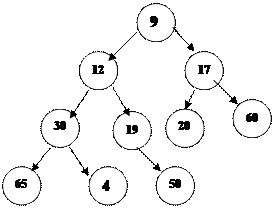 |
А(3)=30 ата-анасы А(8)=4 деген ө зінің ұ рпағ ынан ү лкен. Сондық тан А(3) пен А(8) орындарын ауыстырамыз. (егер екі ұ рпақ тың екеуі де кіші болса, ең кіші баласымен орын аыстырамыз).
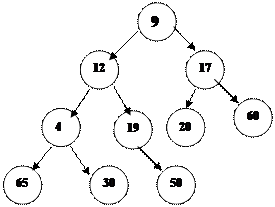 |
Екі дең гейдегі А(2)=17 ата-анасы пирамиданың шартн қ анағ аттандырады. Сондық тан ауыстырулар жү ргізілмейді. Ал А(1)=12 ө зінің А(3)=4 деген баласынан ү лкен болып тұ р. Сондық тан олардың орындарын ауыстырамыз:
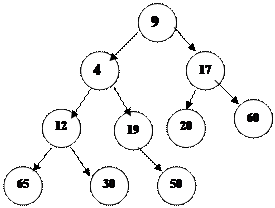 |
Осы процесс тү бірлік тү йінде аяқ талады. А(0)=9 ата –анасы ө зінің А(1)=4 деген ұ рпағ ымен орын ауысады.
 |
Нә тижелік тармақ осы пирамида болады.
Пирамидағ а элемент қ осу
1. Жаң а элемент тізімнің соң ынан қ осылады:
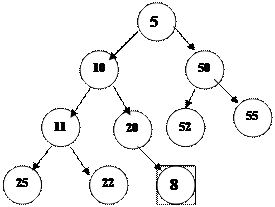 |
2. Егер жаң а элемент ө зінің ата-анасына қ арағ анда кіші мә нге ие болса, онда тү йіннің орнын ауыстырамыз.
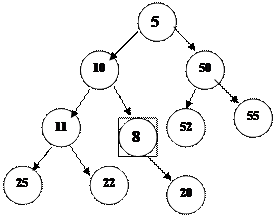 |
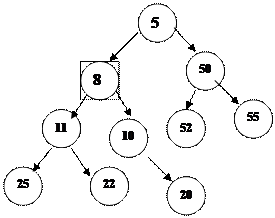 3. Жаң а ата-ана бала ретінде қ арастырылады да одан да ата-ана ү шін пирамидада шарт тексеріледі.
3. Жаң а ата-ана бала ретінде қ арастырылады да одан да ата-ана ү шін пирамидада шарт тексеріледі.
4. Осы процесс ата-ананың жолын қ айталап, жаң а элементтен кіші ата-ананы кезіктіргенде немесе тү бірлі тү йінге келгенде тоқ тайды.
Элементтерді пирамидадан ө шіру
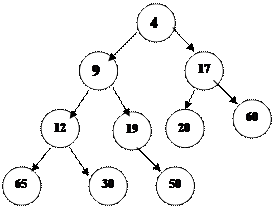
Мә ліметтер қ анашанда тармақ тың тү бірінен ө шіріледі.
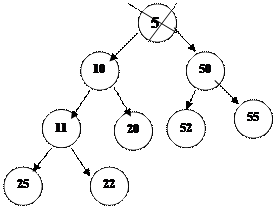 |
1. Тү бірлік тү йінді ө шіріп, оны соң ғ ы тү йінмен алмастыру.
2. Егер жаң а тү бірлік тү йін ө зінің ұ рпақ тарының кез келгенінен ү лкен болса, онда оны ө зінің кіші ұ рпақ тарымен орын ауыстыру керек.
 | |||
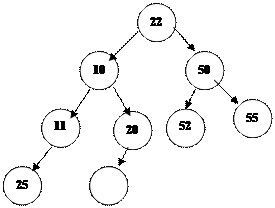 | |||
 3. Кіші ұ рпақ тар бойынша жү ргізілетін осы жол элемент ата-ана ретінде дұ рыс позицияғ а келгенше немесе тізімнің соң ына жеткенше далғ асады.
3. Кіші ұ рпақ тар бойынша жү ргізілетін осы жол элемент ата-ана ретінде дұ рыс позицияғ а келгенше немесе тізімнің соң ына жеткенше далғ асады.
Пирамидалық сұ рыптау
1. Массивті пирамидағ а тү рлендіру.
2. 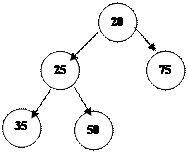 А(0)-ді тізбетеп жоқ қ а шығ ару жә не оны А(n-1), А(n-2) т.с.с А(1)-ге дейін қ осу. Пирамидалық сұ рыптау процесінде кезекті ең кіші элементтер ө шіріліп отырады да, тізбекті тү рде массивтің соң ғ ы жағ ына орналасады. Осылайша, кему реті бойынша сұ рыпта жү ргізіледі. Мысал: А(5)=(50, 20, 75, 35, 25).
А(0)-ді тізбетеп жоқ қ а шығ ару жә не оны А(n-1), А(n-2) т.с.с А(1)-ге дейін қ осу. Пирамидалық сұ рыптау процесінде кезекті ең кіші элементтер ө шіріліп отырады да, тізбекті тү рде массивтің соң ғ ы жағ ына орналасады. Осылайша, кему реті бойынша сұ рыпта жү ргізіледі. Мысал: А(5)=(50, 20, 75, 35, 25).
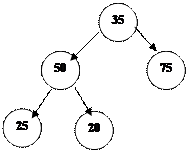
Мысалғ а А(5)=(50, 20, 75, 35, 25)
1. 20-ны ө шіріп, А(4)-ке сақ таймыз:
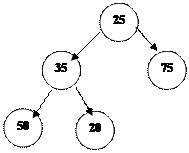 |
2. 25-ті ө шіріп, А(3)-ке қ оямыз:
 |
3. 35-ті ө шіріп, А(2)-ге қ оямыз:
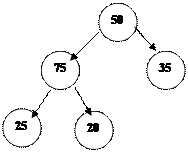 |
4. 50-ді ө шіріп, А(1)-ге қ оямыз:
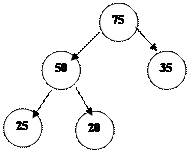 |
Сонымен, тү бірі ғ ана қ алғ андық тан, массив сұ рыпталды.
Есептеу тиімділігі.
n элементтен тұ ратын массив терең дігі k=log2n болатын аяқ талғ ан бинарлық тармақ қ а сә йкес келеді. Массивті пирамидағ а тү рлендіру n/2 операциядан тұ рады. Олардың ә рқ йсысы k салыстырудан артық салыстыруды қ ажет етпейді. Сұ рыптаудың екінші фазасы n-1 операциясын қ ажет етеді. Олардың ә рқ айсысы k салыстырудан тұ рады. Пирамидалық сұ рыптаудың ең жаман жағ дайдағ ы кү рделілігі k*n/2+k*(n-1)=((3n/2)-1) log2n тең болады. Алгоритмнің кү рделілігі мынадай ретке тең: O(n log2n).
Пирамидалық сұ рыптау қ осымша жадыны қ ажет етпейді. Ал мысалғ а турнирлық сұ рыптауғ а қ осымша жаң а массив жасалу қ ажет.
Дә ріс 15.
Балансталғ ан тармақ тар. Графтар.
Мақ саты: Балансталғ ан тармақ тар ұ ғ ымын енгізу. AVL тармақ тары, балансталғ ан тармақ тарғ а қ осу, алып тастау ә рекеттерін тү сіндіру. Графтар. Негізгі ұ ғ ымдары мен анық тамаларын беру. Кө ршілестік матрицасы, инцидиенттік матрицасы тү сініктері.
Негізгі ұ ғ ымдар. Бинарлық тармақ тар алпы мә ліметтерге қ ол жеткізуге арналғ ан. Идеалды яғ ни ең жақ сы жағ дайда тармақ балансталғ ан болады жә не реттілік биіктігі O(nlog2n)-ғ а тең болады. Алайда, кейбір мә ліметтер ү шін тармақ туындағ ан болуы мү мкін. Онда оның биіктігі O(n)-ғ а тең болады жә не мә ліметтерге кіру ә жептә уір ақ ырындайды.
Тармақ балансталғ ан болады сонда тек сонда ғ ана егер ә рбір тү йін ү шін оның екі бұ тағ ының биіктігі бір-бірінен бірге ғ ана айырмашылығ ы болса. Балансталғ ан тармақ тарды AVL тармақ тар деп атайды (Ойлап тапқ андардың фамилиялары бойынша – Адельсон-Венский-Ландис).
Іздеудің бинарлық тармағ ы:
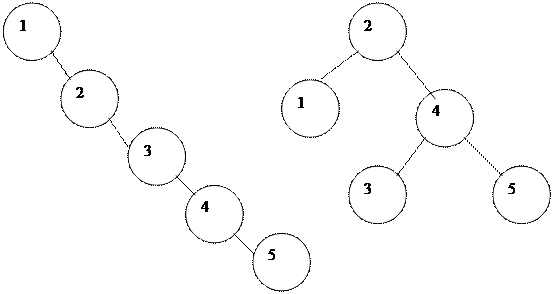 |
AVL тармақ тар берілуі іздеудің бинарлық тармағ ына ұ қ сас болады. Барлық операциялар ұ қ сас тек қ ана тармақ қ а қ ою жә не тармақ тан алып тастау операциялары ө згеше. Сол жақ жә не оң жақ бұ тақ тың арақ атынасы туралы ақ паратты сақ тау ү шін тү йіннің типі анық тамасына ө р і с қ осылады. Ол ө ріс сол жақ жә не оң жақ бұ тақ тың айырмасын кө рсететін баланстық кө рсеткіш. Егер баланс –1-ге тең болса, онда тү йіннің сол жағ ы басады. Себебі, сол жақ бұ тақ тың биіктігі кө п. Ал, баланс оң болса, онда тү йін оң ғ а қ арай тартады. Жалпы биіктігі бойынша балансталғ ан тармақ баланс -1-ге тең болады. Ал AVL тармақ тары [-1; 1] араларында тербеледі.
Балансталғ ан тармақ қ а қ осу
AVL тармақ тардың артық шылығ ы сә йкес қ осу жә не алып тастау алгоритмдермен қ амтамасыз етілген олардың баланстылығ ында болады. Элемент қ осу іздеудің бинарлық тармағ ына ұ қ сас. Яғ ни, сол жақ жә не оң жақ ұ рпақ тары бойынша рекурсивті тү су жү ргізіледі. Бос бұ тақ кезіккенше жү ргізіледі. Одан кейін осы жерде жаң а тү йінді қ осу жү зеге асды.
1. Тармақ та кілт жоқ болғ анша іздеу жолымен жү ре беру.
2. Жаң а тү йін қ осу жә не баланыстылық тың жаң а кө рсеткішін анық тау.
3. Іздеу жолымен қ айтадан жү ру жә не ә рбір тү йін ү шін баланстылық кө рсеткішін тексеру.
Ү ш жағ дай болуы мү мкін. Алғ ашқ ы екеуінде тү йін баланстылық ты сақ тайды. Бұ тақ тар реоргинизациясы қ ажет емес. Тек қ ана берілген тү йіннің баланстылық кө рсеткішін корректілеу керек. Ү шінші жағ дайда тармақ ты қ айта баланстау тү йіннің бірлік немесе екілік айналымын қ ажет етеді.
1-жағ дай. Іздеу бағ ытындағ ы тү йін басынан бастап балансталғ ан деп есептейміз. Яғ ни балнс 0-ге тең. Бұ тақ қ а жаң а элементті қ осқ аннан кейі, тү йін қ осу қ ай жақ бұ тақ қ а жү ргізілгеніне байланысты солғ а немесе оң ғ а тарта бастайды. Егер элемент сол жақ бұ тақ қ а қ осылғ ан болса, онда баланстық кө рсеткіш -1-ге тең, ал оң жақ бұ тақ қ а қ осылғ ан болса, баланстық кө рсеткіші +1-ге тең болады.
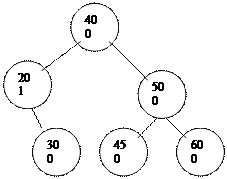 |
Осы балансталғ ан тармақ қ а 55 деген тү йінді қ осамыз:
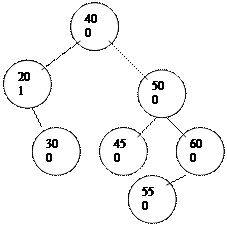 |
2-жағ дай. Тү йіннің бұ тағ ының біреуінің бір жағ ы басым жә не жаң а элемент жең іл бұ тақ қ а қ осылады да, тү йін балансталғ ан болып ө згереді.
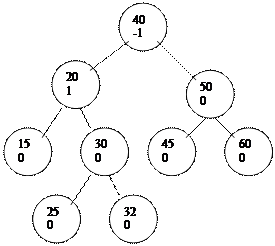 |
55 тү йінін қ осқ аннан кейін:
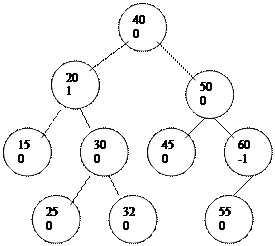 |
3-жағ дай. Тү йіннің бұ тақ тарының бір жағ ы басым, жаң а элемент неғ ұ рлым ауыр жағ ына қ осылады. Ал олай болса, баланстылық шарты бұ зылады. Себебі, баланс [1; 1] шегінен аспуы тиіс. Ал тепе-тең дікті сақ тау ү шін бұ рылыс жасау қ ажет.