
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графтар
|
|
Граф дегеніміз – G=< V, E> жұ бы. Мұ ндағ ы V-тө белердің қ ұ р емес жиыны. E - қ абырғ алар жиыны. Яғ ни, тө белер жұ бы немесе қ абырғ алары жиыны деп аталатын мә ліметтер элементтері жиынынан тұ рады. Тө белер қ алаларды кө рсететін болса, қ абырғ алар арасындағ ы жолдарды кө рсетеді.
 |
1250 900
Егер е жұ птары реттелмеген болса, яғ ни жолдардағ ы қ озғ алыс екі бағ ытта да жү ретін болса, онда граф бағ дарланбағ ан ә йтпесе бағ дарланғ ан деп аталады. Егер қ абырғ алардың бір бө лігі бағ ытталғ ан немесе бағ дарланғ ан болса, мұ ндай графтар аралас графтар деп аталады.
V1, V2,..., Vn тө белерінің тізімі жол деп аталады. Мұ ндағ ы барлық i ү шін 1< =i< =n, Vi, Vi+1 қ абырғ алары болады.
Бағ дарланғ ан графта V1, V2,..., Vn тө белердің тізімі.
V1®V2, V2 ®V3,..., Vn-1 ®Vn бағ ытталғ ан доғ а тү рінде болады. Графтардағ ы жол қ арапайым деп аталады, егер графтардың тө белері ә ртү рлі болса. Жолдың ұ зындығ ы осы жолды қ ұ райтын қ абырғ алардың санына тең болса.
Vi жә не Vj тө белері байланғ ан деп аталады егер, осы тө белер ү шін Vi+1, Vi+2,.., Vj жолы бар болса. Граф байланысшы граф деп аталады егер, оның кез келген тө белер жұ птары ү шін оларды қ осатын қ арапайым жол болса.
Цикл дегеніміз - ұ зындығ ы бірден кем болмайтын бір тө беден басталып сол тө беден аяқ талатын қ арапайым жол.
Графтардағ ы тармақ дегеніміз – бұ л циклсыз графтар. Графтар ө лшенген деп аталады егер, графтың ә рбір қ абырғ асына мә ні немесе салмағ ы жазылса.
Мысалғ а, салмақ ретінде қ алалардың арасындағ ы арақ ашық тық немесе қ андай да бір жұ мыстың жү ргізілу уақ ыты алынады.
Графтарды берудің келесідей ә дістері бар:
1. Инцидиенттік матрицасы.
2. Кө ршілестік матрицасы.
3. Салмақ тық матрицасы.
4. Қ абырғ алар тізімі.
5. Кө ршілестік тізімі.
Қ андай да бір нақ тылы есепті шығ ару ү шін қ олдану қ олайлылығ ына қ арай осы ә дістердің кез келгенін пайдалануғ а болады.
Инцидиенттік матрицасы дегеніміз – размері n´ m болатын матрица. Мұ ндағ ы n-тө белер саны, m-қ абырғ алар саны. Бағ ытталғ ан граф ү шін х, у қ абырғ аларына сә йкес келетін бағ ан, у тө бесіне сә йкес келетін жолда 1 болады. Ал х тө бесіне сә йкес келетін жолда -1 болады, қ алғ ан жолдарда 0 болады. Тұ зақ жағ дайында басқ а сан берілуі мү мкін. Яғ ни, хх болғ анда 2 деген сан беріледі. Мысалы,
1 2 4 5
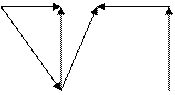
3 6
граф берілген, оның инцидиентті матрицасын жазамыз:
(1, 2) (1, 3) (3, 2) (3, 4) (5, 4) (5, 6) (6, 5)
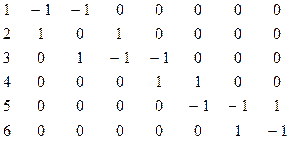
Бағ ытталғ ан граф ү шін х, у қ абырғ асына сә йкес келетін бағ ан х, у тө бесіне сә йкес келетін жолда 1 болады да, қ алғ ан жолдарда 0 болады.
2 4
 1 6
1 6
3 5
(1, 2)(1, 3)(1, 5)(2, 3)(2, 5)(3, 4)(4, 5)(4, 6)(5, 6)
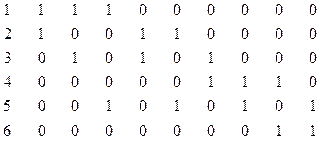
Графты инцидиентті матрица арқ ылы беру ү шін n´ М элемент қ ажет болады жә не олардың кө бі 0 болады. Инцидиентті матрица ЭЕМ-ғ а енгізу мен ө ң деуге қ иын. Сондай-ақ ол қ абырғ алар туралы тура ақ парат бермейді. Х, у қ абырғ асы бар ма деген сұ рақ қ а жауап беру ү шін барлық бағ андарды қ арап шығ у қ ажет.
Кө ршілестік матрицасы
Кө ршілестік матрицасы дегеніміз - ө лшемі n´ М болатын жә не егер i-ші тө бесі j-ші тө бесімен кө ршілес болса мә ні бірге тең болатын, ә йтпесе 0-ге тең болатын матрица.
Бағ ытталмағ ан графтар ү шін х, у қ абырғ асы у, х қ абырғ асына тең болады. Сондық тан олар ү шін кө ршілестік матрицасы ә рқ ашан симметриялы. Оларда алдың ғ ы граф ү шін матрица мынадай:
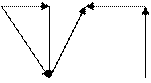 1 2 4 5
1 2 4 5
3 6
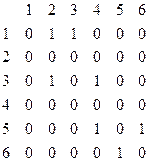
Бағ ытталмағ ан граф ү шін кө ршілестік матрица:
2 4
 1 6
1 6
3 5

Кө ршілес матрица симметриялы болып табылады, сондық тан ЭЕМ-ғ а енгізіп, ө ң деуге қ олайлы.
3 Зертханалық сабақ тар
Зертханалық жұ мыс №1
Тақ ырыбы: Сызық ты байланысқ ан мә ліметтер қ ұ рылымдарын ұ йымдастыру жә не олармен жү ргізілетін амалдар.
Жалпы мә лімет
Массив дегеніміз мә ліметтердің қ ұ рылымдалғ ан жиыны. Ол жалпы аты бар, бір типті элементтердің белгіленген санының реттелген жиынтығ ын сипаттау ү шін қ олданылады. Массив элементтерін белгілеу ү шін массив айнымалысы аты жә не индексі қ олданылады. Жұ мысты орындамас бұ рын массив типті айнымалыларды қ олдануды жә не сипаттау ережелерін ү йрену керек.
Мысалы: Екі ө лшемді массив берілген. Ә рбір жолда оның нольге тең емес элементтерін ретін сақ тай отырып, жолдың басына жазу керек, ал барлық нольге тең элементтерін жол соң ына жазу керек. Жаң а массив жасауғ а болмайды.
Есепті шешу этаптары:
1. Бұ л есепті шешудің алгоритмдерінің біреуінің мә ні массивті жол бойынша қ арап, ә рбір жолда (0: сан) жұ бын тауып, содан кейін олардың ө зара орынын ауыстырып, осылайша жолда мұ ндай жұ птар қ алмағ анғ а дейін жалғ астыруда.
2. Программаның паскальда жазылуы:
3. program маs_1;
var V: array[1..100, 1..100] of integer; m, n, i, j, c: integer; flag: boolean; begin < массив ө лшемін енгізу m*n> < массив ұ яшық тарын толтыру> for i: =1 to m do repeat flag: = true; for j: =1 to n-1 do if (v[i, j]=0) and (v[i, j+1]< > 0) then begin < олардың орынын ауыстыру> flag: = false; end; until flag; < массивты басып шығ ару> readln; end. 4. Алгоритмнің блок-схемасы
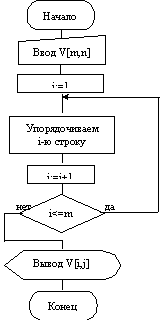
Бірінші жолды реттейміз:
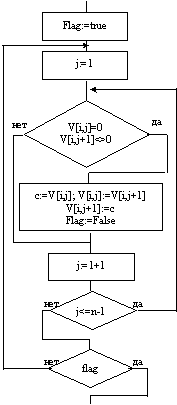
Блок-схеманың алгоритмы бү тіндей:
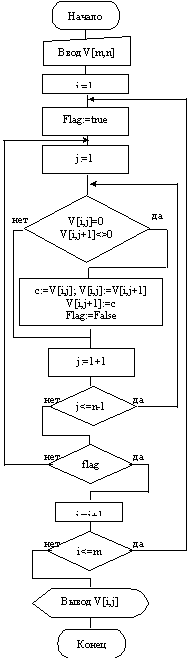
5. Паскальдағ ы программа:
Зертханалық жұ мыс №2
Тақ ырыбы: Ағ аш типті мә ліметтер қ ұ рылымдарын ұ йымдастыру.
Жалпы мә лімет
Тармақ дегеніміз – иеархиялық қ ұ рылым қ ұ ратын элементтер мен қ атынастардың жиынтығ ы.
Тармақ тың элементтері тү йін деп аталады. Ағ аш тә різді қ ұ рылым тү пкі деп аталатын алғ ашқ ы бір тү йіннен басталатын кө птеген тү йіндер жиынтығ ын қ ұ райды.
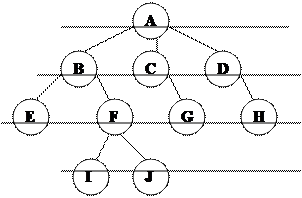 |
0-дең гей 1-дең гей 2-дең гей 3-дең гей
Мұ нда ағ аштың тү бірі дегеніміз – ары қ арай тү бірі болмайтын тө бесі, яғ ни мұ ндағ ы А. Ә рбір тармақ тың бір ғ ана тү бірі болады. Тармақ тың ең тө менгі тү йіндері E, F, G, H жапырақ деп аталады. Егер тармақ тың элементі жапырақ болмаса, онда оны тармақ тың ішкі тү йіні немесе тө бесі деп аталады. Бос тармақ дегеніміз – ешқ андай тө бесі жоқ тармақ ты атаймыз. Балалық тө бесі деп – тармақ та орналасқ ан ө зінің ата-аналық тө бесінен тө мен қ арай тұ рғ ан жә не онымен тікелей байланысқ ан тө бені атаймыз. Мысалғ а, егер i тө бесі F тө бесіне қ атысты балалық тө бесі болса, онда F тө бесі I тө бесіне қ атысты ата-аналық тө бе деп аталады.
Балалық тү йіндер жә не олардың балалық тү йіндері ұ рпақ деп аталады. Мысалғ а, E, F жә не I, J B – тү йінінің ұ рпақ тары.
Тектері бұ л тү йіннің ата-аналары немесе ата-ә желері.
Тармақ тың ә рбір тү йіні осы тү йіннен жә не барлық ұ рпақ тарынан тұ ратын бұ тақ тың тү бірі болып табылады. Мысалы, В тө бесі E, F, I, J дең гейінің тү йіні. Мысалғ а, F тү йіні F, I, J тү йіндерінен тұ ратын бұ тақ тың тү бірі болып табылады. G тү йіні ұ рпақ сыз бұ тақ тың тү йіні. А тү йіні ө зі тармақ болып табылатын бұ тақ тың тү бірі.
Кез келген тү йіннен тү йіннен бастап оның ұ рпақ тарына қ арай жү ру белгілі бір жол бойымен жү зеге асады. Мысалғ а, А тү бірінен бастап F тү йініне дейінгі жол A, B, F тө белерінен ө теді. Кез келген тү йіннен оның ұ рпақ тарына баратын жол жалғ ыз ғ ана болады. Тү йіннің дең гейі дегеніміз – ол тү бірден осы осы тү йінге дейінгі жолдың ұ зындығ ы. Мысалғ а, А тү бірінің дең гейі 0-ғ а тең. Тү бірдің ә рбір баласының дең гейі 1-ге тең. Мысалғ а F тү йіні 2 дең гейдегі ұ зындығ ы 2-ге тең тү йін болып табылады.
Тармақ тың терең дігі дегеніміз – оның кез келген тү йінінің максимальды дең гейі немесе тармақ тың терең дігі дегеніміз ол тү бірден бастап тү йінге дейінгі ең ұ зақ жолдың ұ зындығ ы.
Тармақ тә різді қ ұ рылымды беру ә дістері
Тармақ тарды берудің 4 тү рлі ә дісі бар:
1. графтар
2. кірістірілген жақ шалар
3. кірістірілген жиындар
4. кесінді тізбектер.
1. Графтар. Бә рі А тү йінінен тарайды

2. Кірістірілген жақ шалар:
(A(B(E, F(I, J)), C(G), D(H)))
4. Кірістірілген жиындар.
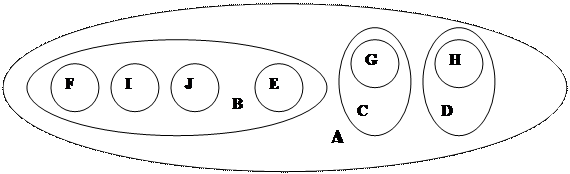 |
4. Кесінді тізбек.
A B E I
 F J
F J
C G
D H
Кө бінесе тармақ тарды бейнелеу ү шін графтар қ олданылады.
Тапсырмалар: Реттелген екілік тармақ жасап, оны экранғ а шығ аратын бағ дарлама қ ұ ру керек.
Зертханалық жұ мыс №3
Тақ ырыбы: Граф типті мә ліметтер қ ұ рылымдарын ұ йымдастыру.
Жалпы мә лімет
Граф дегеніміз – G=< V, E> жұ бы. Мұ ндағ ы V-тө белердің қ ұ р емес жиыны. E - қ абырғ алар жиыны. Яғ ни, тө белер жұ бы немесе қ абырғ алары жиыны деп аталатын мә ліметтер элементтері жиынынан тұ рады. Тө белер қ алаларды кө рсететін болса, қ абырғ алар арасындағ ы жолдарды кө рсетеді.
 |
1250 900
Егер е жұ птары реттелмеген болса, яғ ни жолдардағ ы қ озғ алыс екі бағ ытта да жү ретін болса, онда граф бағ дарланбағ ан ә йтпесе бағ дарланғ ан деп аталады. Егер қ абырғ алардың бір бө лігі бағ ытталғ ан немесе бағ дарланғ ан болса, мұ ндай графтар аралас графтар деп аталады.
V1, V2,..., Vn тө белерінің тізімі жол деп аталады. Мұ ндағ ы барлық i ү шін 1< =i< =n, Vi, Vi+1 қ абырғ алары болады.
Бағ дарланғ ан графта V1, V2,..., Vn тө белердің тізімі.
V1®V2, V2 ®V3,..., Vn-1 ®Vn бағ ытталғ ан доғ а тү рінде болады. Графтардағ ы жол қ арапайым деп аталады, егер графтардың тө белері ә ртү рлі болса. Жолдың ұ зындығ ы осы жолды қ ұ райтын қ абырғ алардың санына тең болса.
Vi жә не Vj тө белері байланғ ан деп аталады егер, осы тө белер ү шін Vi+1, Vi+2,.., Vj жолы бар болса. Граф байланысшы граф деп аталады егер, оның кез келген тө белер жұ птары ү шін оларды қ осатын қ арапайым жол болса.
Цикл дегеніміз - ұ зындығ ы бірден кем болмайтын бір тө беден басталып сол тө беден аяқ талатын қ арапайым жол.
Графтардағ ы тармақ дегеніміз – бұ л циклсыз графтар. Графтар ө лшенген деп аталады егер, графтың ә рбір қ абырғ асына мә ні немесе салмағ ы жазылса.
Мысалғ а, салмақ ретінде қ алалардың арасындағ ы арақ ашық тық немесе қ андай да бір жұ мыстың жү ргізілу уақ ыты алынады.
Графтарды берудің келесідей ә дістері бар:
6. Инцидиенттік матрицасы.
7. Кө ршілестік матрицасы.
8. Салмақ тық матрицасы.
9. Қ абырғ алар тізімі.
10. Кө ршілестік тізімі.
Қ андай да бір нақ тылы есепті шығ ару ү шін қ олдану қ олайлылығ ына қ арай осы ә дістердің кез келгенін пайдалануғ а болады.
Инцидиенттік матрицасы дегеніміз – размері n´ m болатын матрица. Мұ ндағ ы n-тө белер саны, m-қ абырғ алар саны. Бағ ытталғ ан граф ү шін х, у қ абырғ аларына сә йкес келетін бағ ан, у тө бесіне сә йкес келетін жолда 1 болады. Ал х тө бесіне сә йкес келетін жолда -1 болады, қ алғ ан жолдарда 0 болады. Тұ зақ жағ дайында басқ а сан берілуі мү мкін. Яғ ни, хх болғ анда 2 деген сан беріледі. Мысалы,
1 2 4 5

3 6
граф берілген, оның инцидиентті матрицасын жазамыз:
(1, 2) (1, 3) (3, 2) (3, 4) (5, 4) (5, 6) (6, 5)
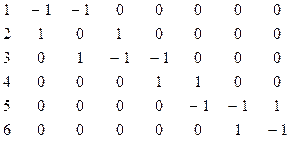
Бағ ытталғ ан граф ү шін х, у қ абырғ асына сә йкес келетін бағ ан х, у тө бесіне сә йкес келетін жолда 1 болады да, қ алғ ан жолдарда 0 болады.
2 4
 1 6
1 6
4 5
(1, 2)(1, 3)(1, 5)(2, 3)(2, 5)(3, 4)(4, 5)(4, 6)(5, 6)

Графты инцидиентті матрица арқ ылы беру ү шін n´ М элемент қ ажет болады жә не олардың кө бі 0 болады. Инцидиентті матрица ЭЕМ-ғ а енгізу мен ө ң деуге қ иын. Сондай-ақ ол қ абырғ алар туралы тура ақ парат бермейді. Х, у қ абырғ асы бар ма деген сұ рақ қ а жауап беру ү шін барлық бағ андарды қ арап шығ у қ ажет.
Кө ршілестік матрицасы
Кө ршілестік матрицасы дегеніміз - ө лшемі n´ М болатын жә не егер i-ші тө бесі j-ші тө бесімен кө ршілес болса мә ні бірге тең болатын, ә йтпесе 0-ге тең болатын матрица.
Бағ ытталмағ ан графтар ү шін х, у қ абырғ асы у, х қ абырғ асына тең болады. Сондық тан олар ү шін кө ршілестік матрицасы ә рқ ашан симметриялы. Оларда алдың ғ ы граф ү шін матрица мынадай:
 1 2 4 5
1 2 4 5
3 6

Бағ ытталмағ ан граф ү шін кө ршілестік матрица:
2 4
 1 6
1 6
3 5
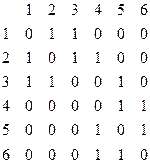
Кө ршілес матрица симметриялы болып табылады, сондық тан ЭЕМ-ғ а енгізіп, ө ң деуге қ олайлы.
Тапсырмалар: Инцидиенттік матрицасы, кө ршілестік матрицасы, салмақ тық матрицасы, қ абырғ алар тізімі, кө ршілестік тізімі ә дістерінің кез-келген біреуін қ олдана отырып есеп шығ ару мысалын кө рсет.
Зертханалық жұ мыс №4
Тақ ырыбы: Іздеу есебін шешу.
Жалпы мә лімет
Массивтер кө бінесе статистикалық мә ліметтер, анық тамалық баслымдар, сө здіктер дайындауда қ олданылады. Ақ паратты іздеудің ең қ арапайым ә дісі бұ л жағ дайда массивтың барлық элементтерін тізбектеп қ арап шығ у болып табылады. Іздеуді жең ілдету мақ сатында массив мазмұ ны белгілі ә дістермен сұ рыпталып, реттеледі.
Мысалы: Реттелген массивте керекті элементті іздеу есебін жә не оны шешу алгоритмін қ арастырайық.
N элементтен тұ ратын нақ ты сандардың А реттелген массивы берілген. Массивте В саны бар ма, егер бар болса оның массивтегі номерін анық тау керек.
А массивында В –ғ а тең элемент бар болып, A[p]=B болатындай қ андай да бір p индексі бар болсын. Кез-келген салыстырудың A[s]< B (1< s< n) нә тижесі бойынша біз p 1 ден s ке дейінгі диапазонда жатыр ма, ә лде s+1 ден n –ге дейінгі диапазонда жатыр ма жылдам анық тай аламыз. Екінші жағ дай A[s]< B тең сіздігі дұ рыс болса орындалады, ал біріншісі дұ рыс емес болса орындалады. Осы салыстырудың қ асиеті ортасынан бө лу алгоритмінде қ олданылады.
Ортасынан бө лу алгоритмі
Алдымен массивтың шеткі элементтері 1 мен n – ді элементті іздеу шекраралары ретінде алады да, осы шекараларды қ адамнан кейін қ адам жү ргізе отырып, бір-біріне сә йкес келгенше жалғ астыра береді: B ны A[s] пен, мұ нда s - шекаралардың арифметикалық ортасының бү тін бө лігі, егер A[s]< B, онда бұ рынғ ы тө менгі шекараны s+1 ге ауыстыру керек, ал жоғ арғ ы шекара ө згеріссіз қ алады, ә йтпесе тө менгі шекара ө згеріссіз қ алып, жоғ арғ ыны s ке ауыстырады. Программа тү рінде бұ л былайша беріледі, фрагментте p мен q айтылғ ан жоғ арғ ы жә не тө менгі шекараларды кө рсетеді:
p: =1; q: =n;
while p< q do
begin
s: =(p+q) div 2;
if a[s]< b then p: =s+1
else q: =s;
end;
Схема тү рінде іздеу процесін келесі схема тү рінде бейнелеуге болады:
+-------------------------0-------------------------------+
¦ +---------------1---------------¦
¦ +-------2--------+ ¦
¦ ¦ +----3---¦ ¦
¦ ¦ +--4-+ ¦ ¦
¦ ¦ +-5+ ¦ ¦ ¦
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Ортасынан бө лу алгоритмі жоғ ары тез ә рекеттілікке ие. Негізінен ортасынан бө лу алгоритмінің идеясы кө птеген алгоритмдер қ ұ руда пайдалы болып табылады. Алгоритмнің негізгі мә ні «бө ліп ал да, ө кімің ді жү ргіз» мағ ынасына келеді.
Бақ ылау сұ рақ тары:
1. Ортасынан бө лу ә дісімен элементті іздеу идеясы неменеге негізделген?
2. Ортасынан бө лу ә дісімен массив элементін іздеу алгоритмін жасаудағ ы ә рекеттер тізбегін сипатта.
Тапсырмалар варианттары:
1. 15 элементті массивті клавиатурадан енгізген бү тін сандардан сақ тау программасын жаса. Массивтың мазмұ ны ө су реті бойынша сұ рыпталады. Осыдан кейін, клавиатурадан бақ ылау саны енгізіледі де, массивте бар-жоғ ы тексеріледі. Бар болса, массивтің элементі номері монитор экранына шығ арылады.
2. Массивте 10 ә ртү рлі бү тін сандарды сақ тауды ұ йымдастыратын программа жаса. Массивтың мазмұ ны ө су реті бойынша сұ рыпталады. Осыдан кейін, клавиатурадан бақ ылау саны енгізіледі де, массивте бар-жоғ ы тексеріледі. Бар болса, массивтың бақ ылау санына тең элементі нольмен ауыстырылады да, массив монитор экранына шығ арылады.
3. Массивте 15 ә ртү рлі бү тін сандарды сақ тауды ұ йымдастыратын программа жаса. Массивтың мазмұ ны кему реті бойынша сұ рыпталады. Осыдан кейін, клавиатурадан бақ ылау саны енгізіледі де, массивте бар-жоғ ы тексеріледі. Бар болса, экранғ а бақ ылау санына дейінгі массив мазмұ ны шығ арылады.
Зертханалық жұ мыс №5
Тақ ырыбы: Іздеу есебін шешу. Толық іздеу: тармақ тар жә не шекаралар ә дістері. Динамикалық программалау.
Жалпы мә лімет
Массивтер кө бінесе статистикалық мә ліметтер, анық тамалық баслымдар, сө здіктер дайындауда қ олданылады. Ақ паратты іздеудің ең қ арапайым ә дісі бұ л жағ дайда массивтың барлық элементтерін тізбектеп қ арап шығ у болып табылады. Іздеуді жең ілдету мақ сатында массив мазмұ ны белгілі ә дістермен сұ рыпталып, реттеледі.
Мысалы: Реттелген массивте керекті элементті іздеу есебін жә не оны шешу алгоритмін қ арастырайық.
N элементтен тұ ратын нақ ты сандардың А реттелген массивы берілген. Массивте В саны бар ма, егер бар болса оның массивтегі номерін анық тау керек.
А массивында В –ғ а тең элемент бар болып, A[p]=B болатындай қ андай да бір p индексі бар болсын. Кез-келген салыстырудың A[s]< B (1< s< n) нә тижесі бойынша біз p 1 ден s ке дейінгі диапазонда жатыр ма, ә лде s+1 ден n –ге дейінгі диапазонда жатыр ма жылдам анық тай аламыз. Екінші жағ дай A[s]< B тең сіздігі дұ рыс болса орындалады, ал біріншісі дұ рыс емес болса орындалады. Осы салыстырудың қ асиеті ортасынан бө лу алгоритмінде қ олданылады.
Ортасынан бө лу алгоритмі
Алдымен массивтың шеткі элементтері 1 мен n – ді элементті іздеу шекраралары ретінде алады да, осы шекараларды қ адамнан кейін қ адам жү ргізе отырып, бір-біріне сә йкес келгенше жалғ астыра береді: B ны A[s] пен, мұ нда s - шекаралардың арифметикалық ортасының бү тін бө лігі, егер A[s]< B, онда бұ рынғ ы тө менгі шекараны s+1 ге ауыстыру керек, ал жоғ арғ ы шекара ө згеріссіз қ алады, ә йтпесе тө менгі шекара ө згеріссіз қ алып, жоғ арғ ыны s ке ауыстырады. Программа тү рінде бұ л былайша беріледі, фрагментте p мен q айтылғ ан жоғ арғ ы жә не тө менгі шекараларды кө рсетеді:
p: =1; q: =n;
while p< q do
begin
s: =(p+q) div 2;
if a[s]< b then p: =s+1
else q: =s;
end;
Схема тү рінде іздеу процесін келесі схема тү рінде бейнелеуге болады:
+-------------------------0-------------------------------+
¦ +---------------1---------------¦
¦ +-------2--------+ ¦
¦ ¦ +----3---¦ ¦
¦ ¦ +--4-+ ¦ ¦
¦ ¦ +-5+ ¦ ¦ ¦
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Ортасынан бө лу алгоритмі жоғ ары тез ә рекеттілікке ие. Негізінен ортасынан бө лу алгоритмінің идеясы кө птеген алгоритмдер қ ұ руда пайдалы болып табылады. Алгоритмнің негізгі мә ні «бө ліп ал да, ө кімің ді жү ргіз» мағ ынасына келеді.
Бақ ылау сұ рақ тары:
1. Ортасынан бө лу ә дісімен элементті іздеу идеясы неменеге негізделген?
2. Ортасынан бө лу ә дісімен массив элементін іздеу алгоритмін жасаудағ ы ә рекеттер тізбегін сипатта.
Тапсырмалар варианттары:
1. 10 бү тін сан массивы беріледі. Оны сұ рыптап, ондағ ы бақ ылау санын тап. Бақ ылау санына дейінгі барлық элементтерді қ арама-қ арсығ а ө згерт.
2. 20 символдан тұ ратын массив берілген. Сұ рыптап, ондағ ы бақ ылау символын тап. Экранғ а бақ ылау символынан бастағ андағ ы элементтерді шығ ар.
20 саннан тұ ратын А массивы берілген. Оны кему реті бойынша орналастыр. Клавиатурадан 2 a жә не b бақ ылау сандарын енгіз. Сандар массивында a мен b аралығ ында жатқ ан сандардың бар-жоғ ын тексер. Бар болса, табылғ ан сандар мен индекстерін экранғ а шығ ар.
Зертханалық жұ мыс №6
Тақ ырыбы: Жылдам іздеу
Жалпы мә лімет
Екілік іздеу тармақ тары программалауда кең таралғ ан. Екілік іздеу тармақ тарының ә рбір тө бесінің мә ні:
1. Оның сол жағ ындағ ы бұ тақ тө бесінің кез келген мә нінен ү лкен немесе тең.
2. Оның оң жақ бұ тағ ының тө бесінің кез келгенінің мә нінен кіші.
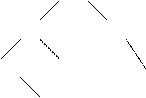
 5 7
5 7
2 8 5 8
0 7 0 6
9 9
6 2
Программада екілік іздеу тармағ ының таралуы бұ л тармақ тарда іздеу ә дістерінің тиімділігінің нә тижесі болып табылады.
Сызық тық қ ұ рылғ ылар ү шін тізбектеліп іздеу алгоритмінің кү рделілігі – О(n) –ғ а тең. Мұ ндағ ы n-қ ұ рылым элементтер саны. Ал аяқ талатын бинарлық тармақ ү шін кү рделілігі – О(log2n)-ғ а тең.
Мысалғ а: 10000 элементтен тұ ратын тізімде тізбектеп іздеуде салыстырудың максимальды саны 10000-ғ а тең болады. Ал аяқ талғ ан тармақ та іздеу 14 салыстырудан аспас еді.
Екілік іздеу тармағ ына элементті осу алгоритмі (тармақ ты қ арау ү немі тү бірден басталады):
4. тармақ қ а қ осылатын мә н ағ ымдағ ы тү йін мә ніне салыстырылады.
5. Егер тармақ қ а қ осылтын мә н ағ ымдағ ы тү йін мә нінен кіші болса, онда келесілер тексеріледі:
а) егер ағ ымдағ ы тү йінде ұ рпақ тар жоқ болса, онда жаң ағ ы мә ні бар тү йінді сол жақ ұ рпақ ретінде бекітеміз.
б) ә йтпесе, (егер ұ рпақ болса) тармақ тың сол жақ бұ тағ ы арқ ылы бір дең гейге тө мендетеміз.
6. Егер тармақ қ а қ осылатын мә н ағ ымдағ ы тү йін мә нінен ү лкен немесе тең болса, келесілер тексеріледі:
а) егер оң жақ тағ ы ағ ымдағ ы тү йінде ұ рпақ тар жоқ болса, онда мә ні бар тү йінді оң жақ ұ рпқ ретінде бекітеміз.
б) ә йтпесе, оң жақ бұ тақ бойымен бір дең гейге тө мендетеміз.
Екілік тармақ тармен жү ргізілетін амалдар
Тармақ ты толығ ымен қ арап ө ту алгоритмі
Тармақ тың тө белерін сұ рыптау алгоритмі – тармақ ты толығ ымен қ арап ө ту алгоритмі деп аталады. Мұ ндай алгоритмдер тү йінде ү ш тү рлі ә рекет жасайды: тү йінге кіреді, сол жақ бұ тақ пен рекурсивті тү рде тө мендейді, рекурсивті тү рде оң жақ бұ тақ пен тө мендейді.
Тармақ ты қ арап шығ удың 3 тү рлі негізгі ә дісі бар:
1. Тура ә діс;
2. Симметриялы ә діс;
3. Кері ә діс;
Тармақ ты толығ ымен қ арап шығ у алгоритмі олардың тү йініндегі ө здерінің ә рекеттерімен байланысты реттерімен ажыратылады.
1. Тура ә діс (жоғ арыдан тө мен қ арай):
- тү йінге кіру;
- сол жақ бұ тақ тан ө ту;
- оң жақ бұ тақ тан ө ту;
 (1) 7
(1) 7
5 8
0 6 9
Екілік тармақ берілген. Бұ л тармақ тағ ы тү йінге кіру реті келесідей болады:
7 5 0 2 6 8 9
2. Симметриялық ә діс (солдан оң ғ а қ арай):
- сол жақ бұ тақ тан жү ріп ө ту;
- тү йінге кіру;
- оң жақ бұ тақ тан жү ріп ө ту;
Берілген (1) тармақ ү шін симметриялық қ арап шығ у келесі тү рде болады:
0 2 5 6 7 8 9
Екілік тармақ ты симметриялық қ арап шығ у ә дісі элементтерді ө су ретімен орналастырды. Осылайша, сұ рыптаудың тағ ы бір алгоритмін ұ сынуғ а болады:
А) массив негізінде сұ рыптау;
В) тармақ ты симметриялық қ арап шығ у ә дісі жү зеге асады;
Мұ ндағ ы ең жақ сы жағ дайда алгоритмнің тиімділігі O(n log2n) болады.
3. Тармақ ты кері қ арай қ арап шығ у ә дісі (тө меннен жоғ арығ а қ арай):
- сол жақ тармақ тан жү ріп ө ту;
- оң жақ тармақ тан жү ріп ө ту;
- тү йінге кіру;
Осы ә діс ү шін тармақ ты жү ріп ө тудің жолы:
2 0 6 5 9 8 7
ө рнектің екілік тармақ тарын қ арап ө туде жоғ арыда берілген ү ш ә діспен мынаны аламыз:
1. Қ арап шығ удың тура ә дісі. ¤рнектерді жазудың префиксті форматына (жоғ арыдан тө менге қ арай) сә йкес келеді.
2. Қ арап шығ удың симметриялық ә дісі ө рнектерді жазудың инфиксті форматина сә йкес келеді.
3. қ арап шығ удың кері ә дісі ө рнектерді жазудың постфиксті форматына сә йкес келеді.
Екілік іздеу тармағ ынан элементті алып тастау.
Тармақ тан элементті алып тастау алгоритмі тармақ тағ ы осы элементтің орналасқ ан орнына тә уелді болады жә не келесі тө рт жағ дайды қ амтиды:
5. Мә ні х-ке тең болатын элемент жоқ.
6. Мә ні х-ке тең болатын элемент терминальды тү йін болып табылады.
7. Мә ні х-ке тең болатын элемент бір ғ ана ұ рпақ ты болады.
8. Мә ні х-ке тең болатын элемент екі ұ рпақ ты болады.
Бір ғ ана ұ рпағ ы болатын элементті алып тастауда ешқ андай кү рделілік жоқ. Мұ ндай ә рекеттер сызық тық тізімдегі элементті алып тастауғ а ұ қ сас болады.
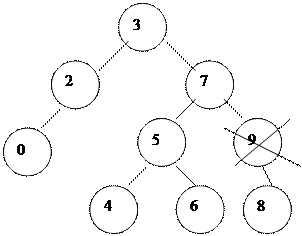 | |||
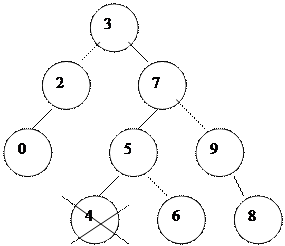 | |||
Егер элемент екі ұ рпақ ты болса, онда екі бағ ытта бір ғ ана сілтемемен кө рсетуге келмейді. Бұ л жағ дайда ө шірілетін элементті ауыстыруғ а тура келеді. Ауыстыратын элемент ү шін оның сол жақ тағ ы ең оң жақ қ ы элемент, ал оң жақ тағ ы ең сол жақ қ ы элемент таң дап алынады (6 жә не 8 ө шірілетін элементке мә ндері жағ ынан жақ ын элементтер).
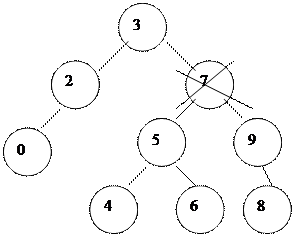 |
Элементі ө шіру алгоритмі. Алгоритм жоғ алғ анда қ арастырылатын 4 жағ дайды қ амтиды:
1-жағ дай: ө шірілетін тү йін табылғ ан жоқ. Яғ ни ө шірук алгоритмі ө з жұ мысын тоқ татады.
2-жағ дай: тү йіннің ұ рпақ тары жоқ. Яғ ни жапырақ болып табылады. Бұ л жағ дайда ата-аналық тү йінді оның бұ тағ ы бос болатындай етіп жаң арту керек.
3-жағ дай:
1. Тү йіннің сол жақ ұ рпағ ы бар, оң жақ ұ рпағ ы жоқ. Яғ ни сол жақ бұ тақ ты оның ата-анасына жалғ астыру керек.
2. Тү йіннің оң жақ ұ рпағ ы бар, сол жақ ұ рпағ ы жоқ. Яғ ни тү йіннің оң жақ бұ тағ ын оның ата-анасына жалғ астыру керек.
4-жағ дай: екі ұ рпағ ы бар тү йінді алып тастау немесе ө шіру. Мұ нда ө шірілетін тү йінді ауыстыру қ ажет. Ауыстыру ү шін сол жақ бұ тағ ы ең оң жақ тағ ы тү йінді таң даймыз.
Келесілерді анық таймыз:
D – ө шірілетін тү йін
P – ө шірілетін элементтің ата-анасы
R – ауыстыратын тү йін
PR – R тү йіннің ата-анасы.
3. D тү йінінің сол жақ бұ тағ ына кө шеміз. Себебі, R ауыстыратын тү йін ө шірілетін D тү йінінен кіші болады.
4. R ауыстыратын тү йін D тү йінінің сол жақ бұ тағ ындағ ы максимальды тү йін болып табылады. Оң жақ бұ тақ бойынша тө мен жылжып, P ауыстыратын тү йінді іздейміз. Жылжу барысында RR ата-аналық тү йінді бақ ылап отырамыз. Мұ нда екі мү мкін жағ дай бар:
3. Оң жақ бұ тақ бос. R ауыстытылатын тү йін ө шірілетін тү йіннің сол жақ баласы болып табылады. Ал PR сә йкесінше D тү йініне кө рсетіледі. Мұ ндай жағ дайда келесі ә рекеттерді орындаймыз:
А) D тү йінінің оң жақ бұ тағ ын R тү йініне қ осамыз.
Б) ¤шірілетін тү йіннің P ата-анасын R тү йініне қ осамыз.
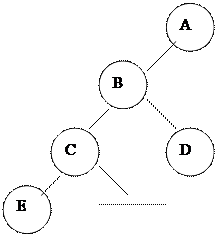 | 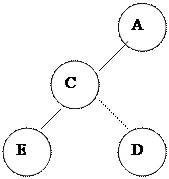 | ||
P P
D R
R PR=D
Оң жақ бұ тақ оң жақ бұ тақ
4. Оң жақ бұ тақ бос емес. Мұ ндай жағ дайда ауыстыратын тү йін жапырақ тық тү йін болады немесе тек қ ана сол жақ бұ тағ ы бар тү йін болады. Келесі ә рекеттерді орындаймыз:
А) R тү йінін тармақ тан бө ліп аламыз.
Б) R тү йінінің ұ рпақ тарын оның ата-аналық РR тү йініне жалғ аймыз. (R-дің сол жақ бұ тағ ы РR-ғ а оң жақ бұ тақ болып жалғ анады).
С) ¤шірілетін D тү йіні R тү йінімен ауыстырылады. Яғ ни D тү йінінің ұ рпақ тары R тү йінінің ұ рпақ тары болып жалғ анады, ал R тү йіні ата-аналық P тү йініне жалғ анады.
Зертханалық жұ мыс №7
Тақ ырыбы: Іздеу есептерінде ағ аштарды қ олдану: бинарлық, кездейсоқ бинарлық, оптималды жә не балансталғ ан іздеу ағ аштары.
Жалпы мә лімет
Іздеу (поиск) екіге бө лінеді:
1. Тізбектеліп іздеу.
2. Бинарлық іздеу.
1. Тізбектеліп іздеу. Тізбектеліп іздеудің мағ ынасы элементтерді тізбекпен таң дап алуды жә не элементтерді кілт мә німен салыстырудан тұ рады.
Функция парамертлер ретінде массивті, элементтер санын жә не кілт мә нін алады. Сә йкес элементтің индексін қ айталайды, егер іздеу сә тсіз болса, -1 мә нін береді. Тізбектеліп іздеу кез келген тізбек ү шін қ олайлы, тізбектеліп іздеудің орталық тиімділігі O(n) тең болады.
2. Бинарлық іздеу.
Бинарлық іздеулер тек қ ана реттелген тізімдер ү шін ғ ана қ олданылады. Мысалы элементтер тұ ратын массив берілсін. Тізімнің басындағ ы жә не соң ындағ ы элементтердің индекстері мынадай low=0 high=n-1 дейін болады. Бинарлық іздеудің алгоритмі:
4. Массивтің ортаң ғ ы элементінің индексін табу: mid=(low+high)/2.
5. Орталық элементтің мә нін кілтпен салыстыру «Key». Егер салыстыру нә тижесінде сә йкестік бар болса, онда mid индексін кілтті табу ү шін қ олданамыз. Егер орталық элемент мә ні кілттен кіші болса, онда қ арастырылып отырғ ан тізімнің оң жағ ындағ ы бө лігінде іздеу жү ргіземіз. Егер керісінше ү лкен болса, онда сол жақ тағ ы бө лігінде іздеу жү ргіземіз.
6. Егер ізделіп отырғ ан элемент тізімде жоқ болса, онда ү зу индикаторын береміз.
Мысалғ а: Бү тін сандар тұ ратын А массиві берілсін. 33 кілті берілген элементі бар табу керек.
Мысал элементтері: А
| -7 |
Low=0
High=8
mid=4
33> A(mid) 0 1 2 3 4 5 6 7 8
| -7 |
mid
Low=5
High=8
mid=6
33> A(mid)
0 1 2 3 4 5 6 7 8
| -7 |
mid
Low=7
High=8
mid=7
33=A(mid)
Сонда тізбектеліп іздеуде 8 салыстыру, ал бинарлық іздеуде 3 салыстыру жү ргізіледі.
Зертханалық жұ мыс №8
Тақ ырыбы: Сұ рыптау есебін шешу. Ішкі жә не сыртқ ы сұ рыптаулар.
Жалпы мә лімет
Қ арапайым таң дау ә дісімен сұ рыптау келесі қ адамдарғ а келтіріледі:
1. Массивтың ең ү лкен элементінің номерін орнату.
2. Массивтың ең ү лкен жә не соң ғ ы элементтерінің орындарын ауыстыру.
3. Соң ғ ы элементті жайына қ алдырып, 1 мен 2 пунктты массивтың қ алғ андарына (соң ғ ы элементсіз) қ айта орындау.
4. 3 пунктты массивтың қ алдығ ы бір элементке дейін қ ысқ арғ анша қ айталау.
Мысалы: сұ рыптау процедурасын программаларды жобалаудың тілінде (псевдокодта) сипаттаймыз.
For i: = n downto 2 do
Begin
Максимальды элементті табу а[1],..., a[i];
Оның индексын k айнымалысында сақ тау;
егер i< > k болса, a[i] мен a[k] орындарын ауыстыру;
End;
Бес элементтен тұ ратын массивтың мә ндері былайша ө згереді: (30, 20, 10, 50, 40)
30 20 10 50 40
30 20 10 40 50
30 20 10 40 50
10 20 30 40 50
10 20 30 40 50
Ең ү лкен элементті іздеу аймағ ының асты сызылғ ан.
Бақ ылау сұ рақ тары:
1. Массивты сұ рыптау деген не?
2. Кему реті бойынша сұ рыптаудың ө спелі рет бойынша сұ рыптаудан айырмашылығ ы неде?
3. Қ арапайым таң дау ә дісімен сұ рыптау арқ ылы массив элементтерін сұ рыптау идеясын сипатта.
4. Бір қ адамды орындау уақ ыты массивтың реттелмеген бө лігінің ө лшеміне неліктен тура пропорционал?
Тапсырмалар варианттары:
Енгізілетін мә ліметтер (алғ ашқ ы массив) пен шығ атын мә ліметтерді (сұ рыпталғ ан массив) бү тін сандардан тұ ратын текстік файл ретінде қ алыптастыру керек.
1. Сұ рыптау процедурасын сұ рыптау элементтердің кему реті бойынша жү ргізілетіндей етіп ө згерт.
2. Бү тін сандардың берілген тізбегі кему реті бойынша сұ рыпталғ ан ба, тексер. Егер жоқ болса, ретте.
3. Массивты сұ рыпта, массивтегі қ айталанбайтын сандардың санын есепте.
4. Сұ рыптау процедурасын I параметры мә ні ә рбір қ адамда ө сетіндей етіп ө згерт.
5. Қ арапайым таң дау ә дісі кө мегімен массивтың жұ п элементтерін сұ рыпта.
6. Қ арапайым таң дау ә дісі кө мегімен массивтың тақ орындарда тұ рғ ан элементтерін сұ рыпта.
7. Қ арапайым таң дау ә дісі кө мегімен массивтың оң элементтерін сұ рыпта.
8. Қ арапайым таң дау ә дісі кө мегімен массивтың теріс элементтерін сұ рыпта.
9. n*m матрицасында бағ андарды ө су реті бойынша сұ рыпта.
10. Футбол командаларының тізімі жә не чемпионатта ә рбір команда алғ ан ұ пайлар саны берілген. Ұ пайлар саны бірдей командалар жоқ екендігі белгілі. Жү лдегерлерді басып шығ ар.
11. Реттелмеген массивте қ айталанатын элементтер болуы мү мкін. Бірдей элементтер тобының ішінен біреуін ғ ана қ алдыру керек.
12. Жарсытың турнирлік кестесі А квадрат матрицасы арқ ылы берілген. Aij ә рбір элементі i командасының j командасының қ ақ пасына соқ қ ан голдар саны. Диагональ бойымен ә рбір команданың орынын орналастыру керек (жең ілістерінің санын алып тастағ андағ ы жең істер саны бойынша, тең тү скен жағ дайда соғ ылғ ан гол мен жіберілген голдардың айырмасы бойынша).
Зертханалық жұ мыс №9
Тақ ырыбы: Сұ рыптау есебін шешу. Сұ рыптау алгоритмдері.
Жалпы мә лімет
Алдың ғ ы алгоритм сияқ ты бұ л алгоритм де жекелеген қ адамдардан тұ рады. Ә рбір қ адамда массивты басынан аяғ ына дейін кө ршілес элементтер жұ птарын салыстыра отырып, жү ріп ө теді. Егер кезекті жұ п талап етілетін тә ртіпті бұ затын болса, онда оның элементтерінің орындарын ауыстырады. Қ адамдарды кезекті жү ріс ешқ андай ауыстыру шақ ырмайтындай болғ анша қ айталай береді.
Мысалы: 5 1 8 4 9 элементтерінен тұ ратын массивты қ арапайым ауыстыру ә дісімен ө спелі тү рде реттейміз. Массивтың ағ ымдағ ы бө лігінің ұ зындығ ы n-k+i, k – қ арап шығ у номері, i – ізделетін жұ птың номері, п – k соң ғ ы жұ птың номері.
.
Бірінші қ арауда барлық массив қ арастырылады.
i = l5 4 8 2 9
> ауыстырамыз
i = 24 5 8 2 9
< ауыстырмаймыз
i = 34 5 8 2 9
> ауыстырамыз
i = 44 5 2 8 9
<
9 ө зінің орнында тұ р.
Екінші қ арау: массивты бірінші элементтен тө ртінші элементке дейін қ арастырамыз.
i = 14 5 2 8 9
< ауыстырмаймыз
i = 24 5 2 8 9
> ауыстырамыз
i = 34 2 5 8 9
< ауыстырмаймыз
8 ө зінің орнында тұ р.
Ү шінші қ арау: массивтың қ арастырылып отырғ ан бө лігі алғ ашқ ы ү ш элементті қ амтиды.
i = 14 2 5 8 9
> ауыстырамыз
i = 22 4 5 8 9
< ауыстырмаймыз
5 ө зінің орнында тұ р.
Тө ртінші қ арау: соң ғ ы жұ пты қ арастырамыз.
i = 12 4 5 8 9
< ауыстырмаймыз
4 ө зінің орнында тұ р.
Ең кіші элемент (2) ү шін тек бірінші орын ғ ана қ алады.
Сө йтіп, массив қ арапайым ауыстыру ә дісімен ө су ретімен орналастырылды. Бұ л ә діс сондай-ақ, «кө піршік ә дісі» деп аталады. Бұ л атау неғ ұ рлым «жең іл» элементтер аз-аздап бетіне, жоғ ары жү зіп шығ атын процестің бейнелік интерпретациясынан келіп шығ ады.
Бақ ылау сұ рақ тары:
1. Массивтың екі элементінің орынын қ алай ауыстырады?
2. Кірістірілген циклдар деген не?
3. Қ арапайым таң дау ә дісі мен қ арапайым ауыстыру ә дісінің айырмашылығ ы қ андай?
Тапсырмалар варианттары:
Енгізілетін мә ліметтер (алғ ашқ ы массив) пен шығ атын мә ліметтерді (сұ рыпталғ ан массив) бү тін сандардан тұ ратын текстік файл ретінде қ алыптастыру керек.
Барлық варианттарғ а «кө піршік» сұ рыптау процедурасын қ олдану керек.
1. Ең жақ сы жә не ең жаман жағ дайлардағ ы орындалғ ан ауыстырулар мен салыстырулар санын есепте.
2. Берілген қ атардың n алғ ашқ ы элементтерін ө су реті бойынша орналастыр. Осы элементтерді кему реті бойынша басып шығ ар.
3. Біздің мысалымызда соң ғ ы екі элемент сұ рыпталғ ан болғ андық тан элемнеттер ретіне ешқ андай ә сер етпейді. Сондық тан, біздің алгоритмді қ андай бір жү рісте элементтер ауыстырылды ма, соны есте сақ тау арқ ылы жақ сартуғ а болады. Егер болмаса, сұ рыптауды аяқ тауғ а болады.
Зертханалық жұ мыс №10
Тақ ырыбы: Сұ рыптау есебін шешу. Сұ рыптау алгоритмдері: таң дау арқ ылы сұ рыптау, жылдам жә не таратпалы сұ рыптау.
Жалпы мә лімет
Массивтерді сұ рыптау алгоритмдері 4-ке бө лінеді:
5. Таң дау арқ ылы сұ рыптау.
6. Ауыстыру арқ ылы сұ рыптау (кө піршік ә діісі).
7. Қ ою арқ ылы арқ ылы сұ рыптау.
8. Тез сұ рыптау.
Сұ рыптау немесе объектілер тізімін реттеу деп осы объектілердің қ андай да бір сызық тық реттілікке қ атысты ө суі мен кемуі бойынша орындауды айтамыз. Сұ рыптаудың мә ні сонда жазулар тізімінің реттілігін кілттік ө ріс мә ндері кемімейтін тізбек қ ұ ратындай етуіміз керек. Басқ а сө збен айтқ анда R1, R2,.., Rn жазулары кілттік мә ндері K1, K2, …, Kn орналасуы керек. Ki1< Ki2< ….< Kin.
Мұ нда реттелген тізбектегі кілттердің бірдей мә ндері бар жазулар бір-бірімен қ атар орындалады. Сұ рыптау ә дістері 2 категорияғ а бө лінеді:
- массивтерді сұ рыптау (ішкі сұ рыптау)
- тізбектелген файлдарды сұ рыптау (сыртқ ы сұ рыптау).
Массивтер ішкі оперативті жадыда орналасады. Оғ ан кез келген уақ ытта тез кіруге болады. Ал сыртқ ы сұ рыптау реттеуге тиісті мә ліметтер кө лемі ө те ү лкен болғ анда мә ліметтердің оперативті жадығ а симай қ алғ анда қ олданылады.
Таң дау кө мегімен сұ рыптау.
А массивінде мә ліметтердің n элементі сақ талғ ан жә не бұ л массив бойынша n-1 жү ріс етеді. 0-ші жү рісте ең кіші элемент таң далады. Ол кейіннен А0 элементпен айырбасталады. Келесі жү рісте тізімнің А1 элементінен бастап реттелмеген бө лігі қ арастырылады. Мұ нда ең кіші элемент тауып алынады да А1-де сақ талады. Ары қ арай А2 ... Аn-1 тізіміндегі ең кіші элемент ізделеді. Табылғ ан мә н А2-мен ауысады. Осылайша, n-1 жү ріс ө теді. Соң ында тізімнің реттелмеген аяғ ы 1 элементке дейін қ ысқ арады. Сол элемент ең ү лкен болып табылады.
Мысалғ а, 50, 20, 40, 75, 35 массив берілген.
0-жү ріс. 20-ны таң даймыз. Оны А0-мен ауыстырамыз (А0=50).
20, 50, 40, 75, 35.
1-жү ріс. 35 таң даймыз. Оны А1-мен орын ауыстырамыз.
20, 35, 40, 75, 50.
2-жү ріс. 40 таң даймыз. Оны А2-мен орын ауыстырамыз.
20, 35, 40, 75, 50.
3-жү ріс. 50 таң даймыз. Оны А3-пен орын ауыстырамыз.
20, 35, 40, 50, 75.
Соң ғ ы қ алғ ан 75 саны ең ү лкен элемент сұ рыпталып шық қ анда:
20, 35, 40, 50, 75.
Сұ рыптау – массив ө лшеміне ғ ана тә уелді салыстырулардың белгіленген санына ие болуы керек. i  -ші жү рісте (A
-ші жү рісте (A 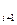 … A
… A 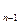 )-ге дейінгі элементтердің салыстырулар саны (n-1-(i+1)+1)=n-i-1 тең болады.
)-ге дейінгі элементтердің салыстырулар саны (n-1-(i+1)+1)=n-i-1 тең болады.
Салыстырулардың жалпы саны мына формуламен анық талады:

Алгоритмнің кү рделілігі – О(n 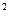 ) тең болады.
) тең болады.
Ауыстыру арқ ылы сұ рыптау.
Ауыстыру арқ ылы сұ рыптау. N элементтен тұ ратын а массивін айырбастау арқ ылы сұ рыптау ү шін немесе кө піршік ә дісімен сұ рыптау ү шін n-ші жү ріс қ ажет. Ә рбір жү рісте кө ршілес екі элемент салыстырылады жә не егер 1-сі ү лкен болса немесе 2-не тең болса, онда бұ л элементтер орындарымен ауысады. ә рбір жү рістің аяғ ында ең кіші элемент ішкі тізімнің жоғ арғ ы жағ ына кө теріліп отырады. Бұ л қ айнап жатқ ан судың ішіндегі ауаның кө бікшесіне ұ қ сас. Сондық тан кө піршік ә дісі деп аталады.
Мысал. Массив:
50, 20, 40, 75, 35
0-жү ріс. 50 мен 20салыстырылады.
20, 50, 40, 75, 35
1-жү ріс. 50 мен 40 салыстырылады
20, 40, 50, 75, 35
2-жү ріс. 50 мен 70 реттелген, сондық тан қ алады.
20, 40, 50, 70, 35
3-жү ріс.75 пен 35 салыстырылады.
20, 40, 50, 35, 75
4-жү ріс. 50 мен 35 салыстырылады
20, 40, 35, 50, 75
5-жү ріс. 40 пен 35 салыстырылады
20, 35, 40, 50, 75
20 мен 30 реттелген
20, 3