Теоретические основы работы

Лабораторная работа № 5

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

ЦЕЛЬ РАБОТЫ

Изучение характеристик вращательного движения твердого тела. Применение основного закона динамики вращательного движения для определения момента инерции тела.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z

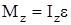(1)

аналогично второму закону Ньютона F = ma. В формуле (1) М_z - момент внешних сил, действующих на тело относительно оси z;
I_z -момент инерции тела относительно оси z; e - угловое ускорение.

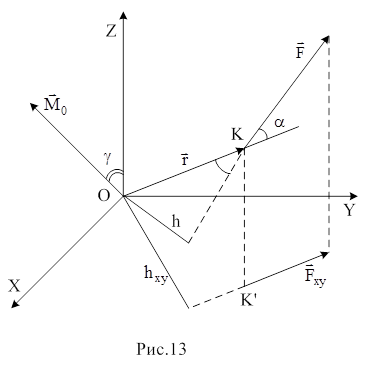Момент силы характеризует вращательное действие силы. Различают момент силы относительно точки (центра) и момент силы относительно оси. Моментом силы (см.рис.13) относительно точки О называется вектор , равный векторному произведению силы 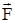и радиуса - вектора 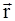, проведенного из точки О в точку К приложения силы:

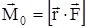. (2)

Модуль вектора равен

, (3)

где h = r× sina - плечо силы, которое равно длине перпендикуляра, опущенного из точки О на направление силы. Вектор направлен перпендикулярно плоскости, проведенной через вектора 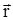и 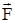в сторону, откуда поворот тела, вызываемый силой 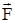, виден против хода часовой стрелки.

Момент силы относительно оси z равен проекции на эту ось момента силы относительно произвольной точки О, лежащей на оси z:

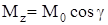. (4)

Момент силы М_z относительно оси - величина алгебраическая. Кроме формулы (4) для вычисления момента силы относительно оси z можно использовать формулу:

, (5)

где 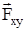- проекция силы 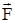на плоскость ОХУ, перпендикулярную оси z; h_xy - плечо силы 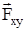(см.рис.13). В формуле (5) знак " +" берется, если с положительного направления оси z поворот тела, вызываемый силой 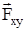, виден против хода часовой стрелки, и знак " -", если по ходу часовой стрелки.

Момент инерции тела I_z относительно оси z является мерой инертности тела при его вращении относительно этой оси и определяется формулой:

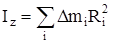, (6)

где 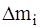- масса материальной точки, удаленной на расстояние R_i от оси z.

Из формулы (6) видно, что момент инерции тела относительно оси равен сумме моментов инерции 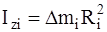отдельных материальных точек тела. Если массу 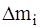каждого малого объема 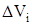выразить через плотность тела r и объема 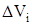точки, то из формулы (6) следует

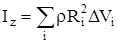. (7)

Предел суммы (7) при - это интеграл по объему тела V:

. (8)

С помощью формулы (8) можно вычислять моменты инерции однородных тел правильной геометрической формы относительно осей, проходящих через центры масс этих тел. В частности, момент инерции однородного прямого круглого цилиндра массой m и радиусом основания R относительно оси z, проходящей через центр масс С этого цилиндра параллельно его боковой поверхности (рис.14 а), равен

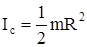. (9)

Если же ось z перпендикулярна боковой поверхности такого цилиндра (рис.14 б), то момент инерции можно найти по формуле

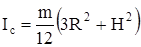, (10)

Для вычисления момента инерции тела относительно произвольной оси z¢ применяется теорема Штейнера (рис.15): момент инерции тела I относительно произвольной оси z¢ равен сумме момента инерции I_с относительно оси z, параллельной данной оси z¢ и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

. (11)

Момент инерции тела сложной формы проще определить экспериментально. Из уравнения (1) получим

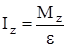. (12)

Момент инерции тела I_z можно найти по формуле (12), если экспериментально оценить момент сил M_z и угловое ускорение e.