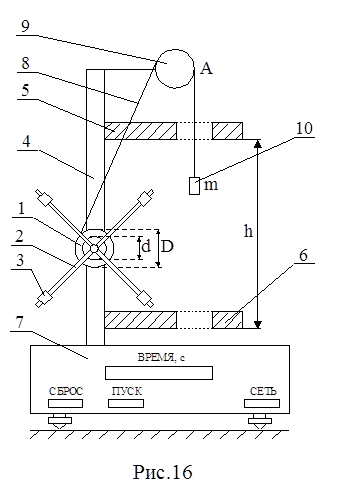
Описание экспериментальной установки. Экспериментальная установка показана на рис. 16.

Экспериментальная установка показана на рис.16.

Маятник Обербека состоит из четырех спиц, укрепленных на втулке под прямым углом друг к другу. На втулке закреплены два шкива 1 с разными диаметрами D и d. Втулка со спицами и шкивами может свободно вращаться относительно горизонтальной оси. Вдоль каждой спицы 2 можно перемещать грузик 3, закрепляя его на расстоянии R от оси вращения. Маятник Обербека и два кронштейна 5 и 6 крепятся к вертикальной стойке 4. Если на шкив 1 намотать нить 8, к ее концу присоединить груз 10 массой m и перекинуть нить через неподвижный блок 9, то, нажимая кнопку " ПУСК", измерить время ускоренного движения груза 10 на расстоянии h с помощью секундомера 7 экспериментальной установки.

Так как начальная скорость груза равна нулю, то ,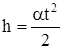
где t - время движения груза. Тогда ускорение груза, направленное вниз, равно

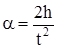. (13)

На груз действует его сила тяжести 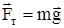и сила натяжения нити 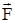. Если на вертикальной оси координат положительное направление выбрать вниз, то проекция второго закона Ньютона 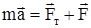на эту ось имеет вид: 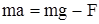. Отсюда сила натяжения нити равна

.

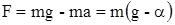Момент силы натяжения, действующий на маятник Обербека, относительно горизонтальной оси z соответственно равен 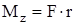, где r - радиус шкива. Тогда

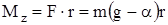. (14)

Под действием момента силы маятник вращается с угловым
ускорением e. Если нить, навитая на шкив, не проскальзывает, то ускорение нити, равное ускорению груза, равно тангенциальному ускорению точек обода шкива 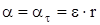. Отсюда

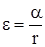. (15)

Подставляя формулы (14) и (15) в формулу (12), найдем общий момент инерции маятника Обербека относительно горизонтальной оси z, проходящей через центр масс маятника

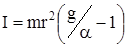. (16)

Подставляя формулу (13) в формулу (16) и учитывая, что
r = d/2, получим формулу для определения момента инерции маятника Обербека относительно оси вращения:

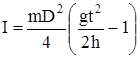. (17)

Если момент инерции крестовины со шкивами относительно оси вращения обозначить I_кр, то общий момент инерции маятника относительно этой оси равен

. (18)

Момент инерции I_Г одного цилиндрического грузика относительно оси вращения находим с помощью формулы (10) и теоремы Штейнера (11):

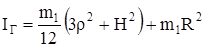, (19)

где m₁ - масса грузика, r, Н - радиус и высота цилиндрического грузика,
R - расстояние центра масс каждого грузика до оси вращения. Подставляя формулу (19) в формулу (18), получим момент инерции маятника относительно оси вращения в виде:

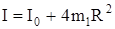, (20)

где .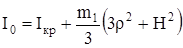

Согласно формуле (20) меняя расстояние R центров грузиков до оси вращения, изменяем общий момент инерции I маятника Обербека.