Включение в модель регрессии фактора времени

В корреляционно-регрессионном анализе устранить воздействие какого-либо фактора можно, если зафиксировать воздействие этого фактора на результат и другие включенные в модель факторы. Этот прием широко используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.

Модель вида относится к группе моделей, включающих фактор времени. Очевидно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только текущие, но и лаговые значения независимой переменной, а также лаговые значения результативной переменной.

Преимущество данной модели по сравнению с методами отклонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исходных данных, поскольку значения у, и х, есть уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры а и b модели с включением фактора времени определяются обычным МНК. Расчет и интерпретацию параметров покажем на примере.

Пример 6.3. Построение модели регрессии с включением фактора времени.

Вернемся к данным предыдущих примеров. Построим уравнение регрессии, описывающее зависимость расходов на конечное потребление у, от совокупного дохода х, и фактора времени. Для расчета параметров уравнения регрессии воспользуемся обычным МНК. Система нормальных уравнений имеет вид:

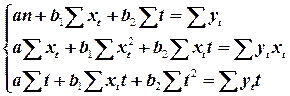
Подставив требуемые суммы, получим:

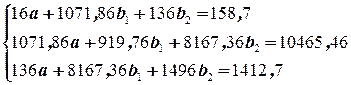
Решая эту систему, получим уравнение регрессии 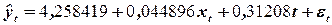. Коэффициент детерминации составит 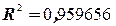, что означает, что данное уравнение достаточно точно описывает реальный процесс. Найдём значение 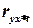, то есть, корреляцию между признаками без учёта фактора времени, используя матрицу парных коэффициентов корреляции 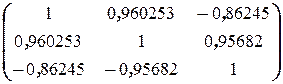, получаем 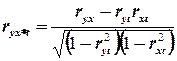=0, 694398. Коэффициент детерминации равен 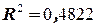Можно сделать вывод, что при использовании фактора времени уравнение достаточно точно описывает реальный процесс.

Проведем сравнительный анализ полученных результатов. Метод отклонения от тренда дает коэффициент детерминации 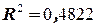, метод последовательных разностей , при использовании фактора времени 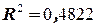. Следовательно, в данном случае метод последовательных разностей показал самую слабую связь между временными рядами.

Автокорреляция в остатках.

Критерий Дарбина-Уотсона.

Рассмотрим уравнения регрессии вида 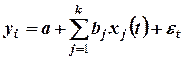, где 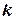- число независимых переменных модели. Для каждого момента времени 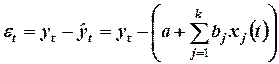. Рассматривая последовательность остатков как временной ряд, можно построить их зависимость от времени. Если каждое следующее значение зависит от предыдущих то это указывает на наличие автокорреляции в остатках.

Автокорреляция остатков может быть вызвана несколькими причинами, имеющими различную природу. Во первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. Во вторых, в ряде случаях причину автокорреляции остатков искать в формулировке модели. Модель может не включать фактор, оказывающий существенное влияние на результат, воздействие которого отражается в остатках.

Существуют два наиболее распространенных метода определения автокорреляции остатков. Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод – использование критерия Дарбина-Уотсона. И расчёт величины 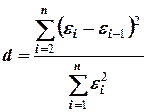. Значение этого критерия табулировано. 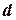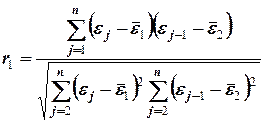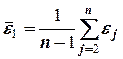Покажем связь между коэффициентом автокорреляции остатков первого порядка, который определяется по формуле , где и 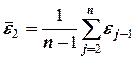. Так как 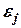остатки то можно предположить и 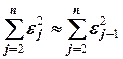. С учётом этих предположений 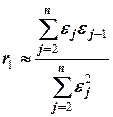. Преобразуем формулу для расчёта критерия Дарбина-Уотсона .

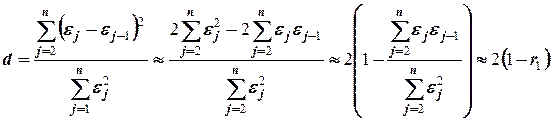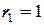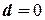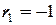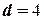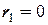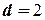Таким образом, если в остатках существует полная положительная автокорреляция и , то . Если в остатках полная отрицательная автокорреляция, то , следовательно . Если автокорреляция остатков отсутствует то и . Следовательно 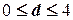. Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза 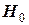об отсутствии автокорреляции остатков. Альтернативные гипотезы 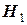и 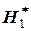состоят, соответственно, в наличии положительной и отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона и для заданного числа наблюдений 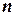, числа переменных в модели 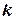и уровня значимости 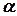. По этим значениям разбивают числовой промежуток 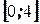на пять отрезков. Принятие и отклонения каждой из гипотез рассматривается в таблице

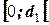
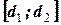
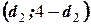
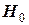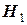Есть положительная автокорреляция остатков. отклоняется, принимается .	Зона неопределённости	Нет оснований отклонять гипотезу 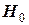. Автокорреляция остатков отсутствует.	Зона неопределённости	Есть отрицательная автокорреляция остатков. 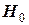отклоняется, принимается .

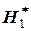Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределённости, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу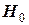

Пример. Проверка гипотезы о наличии автокорреляции в остатках.

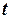
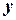
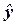
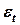
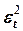
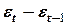
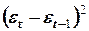
		6, 425	-0, 425	0, 180625
	4, 4	4, 225	0, 175	0, 030625	-0, 6	0, 36
		4, 975	0, 025	0, 000625	0, 15	0, 0225
		9, 075	-0, 075	0, 005625	0, 1	0, 01
	7, 2	7, 175	0, 025	0, 000625	-0, 1	0, 01
	4, 8	4, 975	-0, 175	0, 030625	0, 2	0, 04
		5, 725	0, 275	0, 075625	-0, 45	0, 2025
		9, 825	0, 175	0, 030625	0, 1	0, 01
		7, 925	0, 075	0, 005625	0, 1	0, 01
	5, 6	5, 725	-0, 125	0, 015625	0, 2	0, 04
	6, 4	6, 475	-0, 075	0, 005625	-0, 05	0, 0025
		10, 575	0, 425	0, 180625	-0, 5	0, 25
		8, 675	0, 325	0, 105625	0, 1	0, 01
	6, 6	6, 475	0, 125	0, 015625	0, 2	0, 04
		7, 225	-0, 225	0, 050625	0, 35	0, 1225
	10, 8	11, 325	-0, 525	0, 275625	0, 3	0, 09
				1, 01		1, 22

Значение критерия Дарбина-Уотсона равно .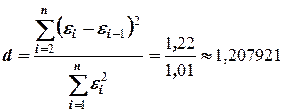

Сформулируем гипотезы:

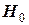- в остатках нет автокорреляции;

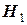- в остатках есть положительная автокорреляция;

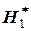- в остатках отрицательная автокорреляция.

Зададим уровень значимости 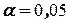. По таблицам значений критерия Дарбина-Уотсона определим для числа наблюдений 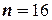и числа независимых переменных 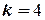критические значения 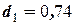и 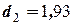. Так как расчётное значение критерия 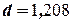больше и меньше 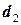то есть попадаем в критическую область, следовательно есть незначительная положительная автокорреляция.