
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связь энтропии и вероятности системы
|
|
Увеличение энтропии сопровождается ростом беспорядка молекулярного состояния вещества. Например, переход от кристаллического состояния вещества к жидкому и газообразному сопровождается понижением упорядоченности и ростом беспорядка в расположении и поведении частиц, следовательно повышением энтропии.
Более беспорядочное состояние является более вероятным. Количественно хаотичность характеризуется термодинамической (статистической) вероятностью. Система может находиться в разных микросостояниях. Под микросостоянием системы подразумевают расположение и свойства отдельных частиц в конкретный момент времени. Общее число равновероятных микросостояний называют термо-динамической вероятностью и обозначают W.
Например, при смешении 2-х систем, состоящих каждая из 4-х молекул, число комбинаций (микросостояний) будет равен 70, т.е. 8 молекул могут распреде-ляться 70 различными способами (расположениями). Шанс всем четырем исход-ным молекулам собраться в начальном положении составляет 1/70.
Значит, чем больше частиц составляет систему, тем больше термодинамическая вероятность, т.е. с ростом числа микросостояний системы возрастает и её энтро-пия, а значит и вероятность протекания процесса. Связь энтропии с термодинами-ческой вероятностью выражается уравнением Л.Больцмана (1872 г.):
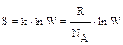
Из него следует, что энтропия есть мера вероятности пребывания системы в данном состоянии.
Таким образом, статистический характер второго закона термодинамики заключается в том, что он является законом вероятности, применяемый к системам, состоящим из большого числа частиц.
Энтропию можно рассчитать по формуле Больцмана. Однако, для систем с большим количеством частиц величину вероятности определить очень трудно или невозможно. Так как энтропия является функцией состояния, её изменение можно вычислить по закону Гесса: DS = S2 – S1.