
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общие сведения. Одним из основных параметров электрических колебаний, определяющих состояние колебательного процесса в любой заданный момент времени
|
|
Одним из основных параметров электрических колебаний, определяющих состояние колебательного процесса в любой заданный момент времени, является фаза. Наряду с фазой одного колебания интерес представляет соотношение фаз двух колебаний. Необходимость в измерениях этих параметров возникает при исследовании усилителей, фильтров, линейных цепей, градуировке фазовращателей, снятии фазочастотных характеристик различных радиотехнических устройств и т.п.
Понятие «фаза» характеризует гармоническое (синусоидальное) колебание в любой конкретный момент времени. Для гармонического колебания u1(t) = Um1sin(ω t + φ 1), имеющего амплитуду Um1 и круговую частоту ω, текущая (мгновенная) фаза в любой момент времени t представляет собой весь аргумент функции φ (t) = ω t + φ 1, где φ 1 — начальная фаза.
Фазовым сдвигом Δ φ двух гармонических сигналов одинаковой частоты
u1(t) = Um1sin(ω t + φ 1) и u2(t) = Um2sin(ω t + φ 2) называют модуль разности их начальных фаз
Δ φ = |φ 1 - φ 2| 7.1)
Общепринято величину φ 1 - φ 2 называть разностью фаз двух сигналов. Если начальные фазы φ 1 и φ 2 сигналов остаются неизменными, то фазовый сдвиг Δ φ не зависит от времени.
Для двух гармонических колебаний с разными круговыми частотами ω 1 ω 2 и начальными фазами φ 1, φ 2, у которых нулевые значения амплитуд при переходе через ось абсцисс сдвинуты на интервал времени τ, разность фаз Δ φ = (ω 1 - ω 2) τ + φ 1 - φ 2.
Для негармонических колебаний понятие фазового сдвига заменяют понятием их сдвига во времени. В этом случае измеряют время задержки одного сигнала относительно другого.
В зависимости от конкретной измерительной задачи и диапазона частот, в котором производятся измерения, требования к точности измерения фазового сдвига могут быть разными — от достаточно грубых измерений (с погрешностью измерения 1...5° до весьма точных (0, 01°).

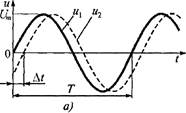
Рис. 7.1. Графики двух сигналов с одинаковыми периодами:
а — гармонических; б — гармонического и негармонического
Измерение разности фаз колебаний с разными частотами редко представляет практический интерес. Поэтому обычно решают задачу измерения разности фаз двух гармонических колебаний с равными частотами. При этом фазовый сдвиг удобно представить в виде зависимости от сдвига сигналов во времени Δ t, соответствующего их идентичным фазам. В частности, для двух гармонических сигналов u1(t)=Umsinω t и u2(t))=Umsinω ( t - Δ t), имеющих одинаковый период Т = 2π / ω (рис. 7.1, а), фазовый сдвиг в радианах
| (7.2) |
Δ φ = ω Δ t = 2π Δ t/T.
Два сигнала с одинаковыми частотами называют синфазными, находящимися в квадратуре и противофазными, если фазовый сдвиг между ними равен 0, π /2 и π соответственно. Применительно к периодическим гармоническому и негармоническому сигналам (рис. 7.1, б) и двум негармоническим сигналам с одинаковым периодом Т используют понятие об их сдвиге (задержке) во времени Δ t.
Измерение фазового сдвига осуществляют приборами, называемыми фазометрами, а в качестве мер сдвига применяют фазовращатели, т.е. линейные четырехполюсники, у которых выходной сигнал сдвинут по фазе относительно входного. Фазовращатели бывают регулируемыми и нерегулируемыми.
Для измерения фазового сдвига применяют различные методы измерений: осциллографические, компенсационный, преобразования фазового сдвига во временной интервал, цифровой (дискретного счета), преобразования частоты. Приборы для измерений фазового сдвига, реализующие перечисленные способы (кроме осциллографических), представлены аналоговыми и цифровыми электронными фазометрами, обеспечивающими измерения в диапазоне от инфразвуковых до высоких частот.