
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: Перевод чисел из одной позиционной системы счисления в другую
|
|
Задача перевода чисел из одной позиционной системы счисления в другую является одной из главных в компьютерной арифметике. Ее можно сформулировать следующим образом: требуется перевести некоторое число (X), записанное в позиционной системе счисления с основанием (k1), в такую же систему счисления, имеющую основание (k2).
Другими словами: по изображению операнда (X) в системе счисления с основанием (k1) найти изображение (Y) того же операнда в системе с основанием (k2).
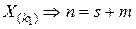 . (2.18)
. (2.18)
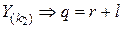 . (2.19)
. (2.19)
Существуют 2 группы методов перевода: табличные и расчетные.
1.Табличные методы. В простейшем случае в памяти компьютерной системы хранится таблица соответствия между всеми числами в системах счисления с основаниями (k1) и (k2), а сама процедура перевода сводится к обращению к этой таблице. Плюс табличных методов перевода заключается в высокой скорости перевода. Минус табличных методов перевода заключается в том, что размеры такой таблицы и, следовательно, занимаемый ею объем памяти, часто оказываются технически неприемлемыми. Поэтому с целью уменьшения занимаемого объема памяти в ней хранят только таблицы соответствия цифр заданных систем счисления и весов их разрядов. Перевод чисел осуществляется путем обращения к этим таблицам и выполнения операций умножения и сложения в соответствии с выражением для КЭЧ. Если, например, числа в системе с основанием (k1) представлены (n - разрядами), то по первому варианту размерность таблицы, сохраняемой в памяти, определяется (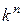 ) строками, а по второму варианту - (k1+n+1) строками.
) строками, а по второму варианту - (k1+n+1) строками.
2.Расчетные методы. В общем виде решение задачи перевода можно представить как нахождение коэффициентов (yj) нового ряда, изображающего число в системе счисления с основанием (k2).
Тривиальным методом решения является. Основная трудность - в выборе максимальной степени (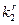 ), которая все еще содержится в числе (X).
), которая все еще содержится в числе (X).
Все действия должны выполняться по правилам (k1-арифметики), т.е. по правилам исходной арифметики. После нахождения максимальной степени основания проверяют «вхождение» в заданное число всех степеней нового основания, меньших максимального. Каждая из отмеченных степеней может входить в ряд не более 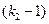 раз, что определяется условием:
раз, что определяется условием:
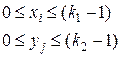 (2.20)
(2.20)
Для перевода операнда (X) в систему с основанием (k2) необходимо записать (X) в форме для вычисления количественного эквивалента, далее заменить цифры (xi) и основания (k1) их эквивалентами в системе с основанием (k2), а потом вычислить полученное выражение по правилам арифметики в системе с основанием (k2). Этот алгоритм удобно использовать в случае, когда (k1< k2), причем (k2) соответствует системе счисления, где просто и " привычно" выполняются операции сложения и умножения (например, десятичной системе). Для упрощения вычислений при этом используют схему Горнера, в соответствии с которой формула для КЭЧ преобразуется путем многократного вынесения за скобки:
Y=(...((xs-1k1+xs-2)k1+xs-3)k1+...+x1)k1+x0+…+(..(((0+x-m) k1-1 +
+x-m+1)k1-1+x-m+2)k1-1+...+x-1)k1-1. (2.21)
Отсюда видно, что для получения целой части числа необходимо выполнить (s) шагов вычислений, а для получения дробной - (m).
Т.е., алгоритм МНЗ, по существу, состоит из двух алгоритмов, а именно: перевода целого числа, выполняемого в соответствии с рекуррентной формулой
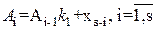 (2.22)
(2.22)
где А0=0, As - целая часть исходного числа в системе счисления с основанием (k2); и перевода дробей по рекуррентной формуле:
 (2.23)
(2.23)
где В0=0, Вm - дробная часть исходного числа в системе с основанием
(k2 ).
Рассмотренный алгоритм не имеет каких-либо теоретических ограничений на область своего применения.
Однако при переводе целых чисел в системы с " непривычными" основаниями, особенно в случае (k1> k2), использование этого алгоритма связано с весьма громоздкими вычислениями.
Поэтому на практике используют отдельные алгоритмы перевода целых чисел и правильных дробей.
В случае (k1> k2). Целое число (X) запишем в системе с основанием (k2) с использованием схемы Горнера:
Y=(…((yr-1k2+yr-2)k2+yr-3)k2+…+y1)k2+y0. (2.24)
Правую часть выражения разделим на величину основания (k2). В результате получим первый остаток (y0) и целую часть:
Y=(…((yr-1k2+yr-2)k2+yr-3)k2+…+y1). (2.25)
Разделив целую часть на(k2), найдем второй остаток(y1).
Повторяя процесс деления r раз, получим последнее целое частное, которое, по условию, меньше основания системы счисления (k2) и является старшей цифрой числа, представленного в системе с основанием (k2).
Правило перевода целых чисел из одной позиционной системы счисления в другую:
- для перевода целого числа в новую систему его надо последовательно делить на основание новой системы счисления до тех пор, пока не получится частное, у которого целая часть равна (0).
Число в новой системе счисления записывается из остатков от последовательного деления, причем последний остаток будет старшей цифрой нового числа.
Алгоритмперевода целых чисел из одной позиционной системы счисления в другую можно сформулировать следующим образом:
- операнд (X) необходимо делить на (k2) по правилам целочисленного деления в исходной системе с основанием (k1) до получения остатка.
Если частное от такого деления не нуль, то далее частное рассматривается как делимое и процесс деления на (k2). продолжают.
Как только очередное частное станет равным нулю, процесс деления прекращают.
Остаток, полученный при первом делении на (k2), представляет собой цифру результата с весом (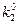 ), остаток от второго деления - цифру результата с весом (
), остаток от второго деления - цифру результата с весом (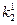 ) и т.д.
) и т.д.
Последний остаток является старшей цифрой результата.
Например: необходимо перевести из десятичной системы счисления в двоичную систему счисления целое число А = 53(10).
Решение: произведем последовательное деление исходного числа (53(10)) на основание новой системы счисления (2). Перевод целого числа А = 53(10) из десятичной системы счисления в двоичную систему счисления, приведен на рис. 2.14:
Рисунок 2.14 - Перевод целого числа А = 53(10) из десятичной системы счисления в двоичную систему счисления
Из сформулированного выше правила при перевод целого числа А = 53(10) из десятичной системы счисления в двоичную систему счисления получим:
53(10) – 110101(2).
Например: необходимо перевести из десятичной системы счисления в троичную систему счисления целое число А = 53(10).
Решение: произведем последовательное деление исходного числа (53(10)) на основание новой системы счисления (3). Перевод целого числа А = 53(10) из десятичной системы счисления в троичную систему счисления, приведен на рис. 2.15:
Рисунок 2.15 - Перевод целого числа А = 53(10) из десятичной системы счисления в троичную систему счисления
Из сформулированного выше правила при перевод целого числа А = 53(10) из десятичной системы счисления в троичную систему счисления получим:
53(10) – 1222(3).
Например: необходимо перевести из десятичной системы счисления в пятеричную систему счисления целое число А = 53(10).
Решение: произведем последовательное деление исходного числа (53(10)) на основание новой системы счисления (5). Перевод целого числа А = 53(10) из десятичной системы счисления в пятеричную систему счисления, приведен на рис. 2.16:
Рисунок 2.16 - Перевод целого числа А = 53(10) из десятичной системы счисления в пятеричную систему счисления
Из сформулированного выше правила при перевод целого числа А = 53(10) из десятичной системы счисления в пятеричную систему счисления получим:
53(10) - 203(5).
Например: необходимо перевести из десятичной системы счисления в восьмеричную систему счисления целое число А = 53(10).
Решение: произведем последовательное деление исходного числа (53(10)) на основание новой системы счисления (8). Перевод целого числа А = 53(10) из десятичной системы счисления в восьмеричную систему счисления, приведен на рис. 2.17:
Рисунок 2.17 - Перевод целого числа А = 53(10) из десятичной системы счисления в восьмеричную систему счисления
Из сформулированного выше правила при перевод целого числа А = 53(10) из десятичной системы счисления в восьмеричную систему счисления получим:
53(10) - 65(8).
Например: необходимо перевести из десятичной системы счисления в шестнадцатеричную систему счисления целое число А = 53(10).
Решение: произведем последовательное деление исходного числа (53(10)) на основание новой системы счисления (16). Перевод целого числа А = 53(10) из десятичной системы счисления в шестнадцатеричную систему счисления, приведен на рис. 2.18:
Рисунок 2.18 - Перевод целого числа А = 53(10) из десятичной системы счисления в шестнадцатеричную систему счисления
Из сформулированного выше правила при перевод целого числа А = 53(10) из десятичной системы счисления в шестнадцатеричную систему счисления получим:
53(10) - 35(16).
При переводе из не десятичной системы счисления в десятичную систему счисления, то ввиду ее не привычности для человека производство в ней арифметических действий значительно затруднено. В этом случае для преобразования чисел необходимо воспользоваться формулой (2.6):
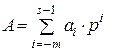 .
.
Например: перевести из двоичной системы счисления в десятичную систему счисления целое число А = 110101(2).
Решение: Запишем число (А) в виде суммы произведений степеней основания на соответствующую цифру в десятичной системе счисления:
А = 110101(2) = 1∙ 25 + 1∙ 24 + 0∙ 23 + 1∙ 22 + 0∙ 21 + 1∙ 20 = 1∙ 32 + 1∙ 16 + 1∙ 25 + 0∙ 8 + 1∙ 4 + 0∙ 2 + 1∙ 1 = 32 + 16 + 0 + 4 + 0 + 1 = 53(10).
Таким образом, получаем: 110101(2) - 53(10).
Например: перевести из троичной системы счисления в десятичную систему счисления целое число А = 1222(3).
Решение: Запишем число (А) в виде суммы произведений степеней основания на соответствующую цифру в десятичной системе счисления:
А = 1222(3) = 1∙ 33 + 2∙ 32 + 2∙ 31 + 2∙ 30 = 1∙ 27 + 2∙ 9 + 2∙ 3 + 2∙ 1 = 27 + 18 + 6 + 2 = 53(10).
Таким образом, получаем: 1222(3)- 53(10).
Например: перевести из пятеричной системы счисления в десятичную систему счисления целое число А = 203(5).
Решение: Запишем число (А) в виде суммы произведений степеней основания на соответствующую цифру в десятичной системе счисления:
А = 203(5) = 2∙ 52 + 0∙ 51 + 3∙ 50 = 2∙ 25 + 0∙ 5 + 3∙ 1 = 50 + 0 + 3 = 53(10).
Таким образом, получаем: 203(5)- 53(10).
Например: перевести из восьмеричной системы счисления в десятичную систему счисления целое число А = 65(8).
Решение: Запишем число (А) в виде суммы произведений степеней основания на соответствующую цифру в десятичной системе счисления:
А = 65(8) = 6∙ 81 + 5∙ 80 = 48 + 5 = 53(10).
Таким образом, получаем: 65(8)- 53(10).
Например: перевести из шестнадцатеричной системы счисления в десятичную систему счисления целое число А = 35(16).
Решение: Запишем число (А) в виде суммы произведений степеней основания на соответствующую цифру в десятичной системе счисления:
А = 35(16) = 3∙ 161 + 5∙ 160 = 48 + 5 = 53(10).
Таким образом, получаем: 35(16)- 53(10).
При переводе из недесятичной системы счисления в недесятичную систему счисления с основанием степени двойки, например если необходимо перевести число из двоичной системы счисления в систему счисления, основанием которой является степень двойки, достаточно объединить цифры двоичного числа в группы по столько цифр, каков показатель степени.
Например, если перевод осуществляется в восьмеричную систему счисления, то группы будут содержать три цифры (8 = 23), такая группа называется триадой. Если перевод осуществляется в шестнадцатеричную систему счисления, то группы будут содержать четыре цифры (16 = 24), такая группа называется тетрадой. В целой части числа группировка производится справа налево, в дробной части – слева направо. Если в последней группе недостает цифр, то дописываются нули: в целой части – слева, в дробной – справа. Затем каждая группа заменяется соответствующей цифрой новой системы счисления.
Например: необходимо из двоичной системы счисления перевести в восьмеричную систему счисления целое число: А = 110101(2).
Решение: исходя из вышесказанного, разобьем целое число: А = 110101(2) на триады и получим рис.2.19:
| 22 | 21 | 20 | 22 | 21 | 20 | |
Рисунок 2.19 - Перевод целого числа А = 110101(2) в восьмеричную систему счисления
Таким образом, получаем: 110101(2) - 65(8).
Например: необходимо из двоичной системы счисления перевести в шестнадцатеричную систему счисления целое число: А = 110101(2).
Решение: исходя из вышесказанного, разобьем целое число: А = 110101(2) на тетрады и получим рис.2.20:
| 23 | 22 | 21 | 20 | 23 | 22 | 21 | 20 | |
Рисунок 2.20 - Перевод целого числа А = 110101(2) в шестнадцатеричную систему счисления
Таким образом, получаем: 110101(2) - 35(16).
При переводе из недесятичной системы счисления в недесятичную систему счисления с основанием степени двойки, например если необходимо перевести число из восьмеричной системы счисления в шестнадцатеричную систему счисления, необходим промежуточный перевод в двоичную систему счисления. Сначала сформировать триады, а затем тетрады. То же самое, если необходимо перевести число из шестнадцатеричной системы счисления в восьмеричную систему счисления необходим промежуточный перевод в двоичную систему счисления. Сначала сформировать тетрады, а затем триады.
Например: необходимо из восьмеричной системы счисления перевести в шестнадцатеричную систему счисления целое число: А = 65(8).
Решение: исходя из вышесказанного, переведем сначала целое число: А = 65(8) в двоичную систему счисления, разбив его на триады, а затем триады преобразовав в тетрады получим число в шестнадцатеричной системе счисления рис.2.21:
Рисунок 2.21 - Перевод из восьмеричной системы счисления в шестнадцатеричную систему счисления целого числа А = 65(8)
Таким образом, получаем: 65(8) - 35(16).
Например: необходимо из шестнадцатеричной системы счисления перевести в восьмеричную систему счисления целое число: А = 35(16).
Решение: исходя из вышесказанного, переведем сначала целое число:
А = 35(16) в двоичную систему счисления, разбив его на тетрады, а затем тетрады преобразовав в триады получим число в восьмеричной системе счисления рис.2.22:
Рисунок 2.22 - Перевод из шестнадцатеричной системы счисления в восьмеричную систему счисления целого числа А = 35(16)
Таким образом, получаем: 35(16) - 65(8).
При переводе из десятичной системы счисления двоично-десятичную систему счисления подразумевают, что двоично-десятичная система счисления представляет собой систему с основанием (10), цифры которой закодированы в виде четырехразрядных двоичных чисел (тетрад), либо с естественным порядком весов (8-4-2-1), либо с искусственным порядком весов.
Например: необходимо из десятичной системы счисления перевести в двоично-десятичную систему счисления целое число: А = 118(10).
Решение: исходя из вышесказанного, при переводе целого десятичного числа: А = 118(10) в двоично-десятичную систему счисления, необходимо разбить его на тетрады рис. 2.23:
| 23 | 22 | 21 | 20 | 23 | 22 | 21 | 20 | 23 | 22 | 21 | 20 | |
Рисунок 2.23 - Перевод из десятичной системы счисления в двоично-десятичную систему счисления целого числа А = 118(10).
Таким образом, получаем: 118(10) - 100011000(2-10).
Например: необходимо из двоично-десятичной системы счисления перевести в десятичную систему счисления целое число: А = 100011000(2-10).
Решение: исходя из вышесказанного, при переводе целого двоично-десятичного числа: А = 100011000(2-10).в десятичную систему счисления, необходимо разбить его на тетрады рис. 2.24:
| 23 | 22 | 21 | 20 | 23 | 22 | 21 | 20 | 23 | 22 | 21 | 20 |
Рисунок 2.24 - Перевод из двоично-десятичной системы счисления в десятичную систему счисления целого числа А = 100011000(2-10)
Таким образом, получаем: 100011000(2-10) - 118(10)
При переводе из недесятичной системы счисления в недесятичную систему счисления например, если необходимо перевести число из пятеричной системы счисления в троичную систему счисления, необходим промежуточный перевод в десятичную систему счисления.
Например: перевести из пятеричной системы счисления в троичную систему счисления целое число А = 203(5).
Решение: Исходя из вышесказанного сначала необходимо целое число:
А = 203(5) записанное в пятеричной системы счисления, перевести в десятичную систему счисления, а затем полученное число из десятичной системы счисления перевести в троичную систему счисления.
Действие №1: А = 203(5) - 10.
А = 203(5) = 2∙ 52 + 0∙ 51 + 3∙ 50 = 2∙ 25 + 0∙ 5 + 3∙ 1 = 50 + 0 + 3 = 53(10).
Действие №2: А = 53(10) – 3, рис.2.25:
Рисунок 2.25 - Перевод целого числа А = 53(10) из десятичной системы счисления в троичную систему счисления
Таким образом, получаем: 203(5) - 1222(3).
Правило перевода правильной дроби из одной позиционной системы счисления в другую.
Пусть правильная (рх – ичная) дробь А(рх) уже переведена и представлена в новой системе счисления с основанием (р):
А(рх) = а1 ∙ р-1 + а2 ∙ р-2 + а3 ∙ р-3 +….+ аn ∙ р-n. (2.26)
где а1 - целая часть первого произведения;
А(рх1) = а2 ∙ р-1 + а3 ∙ р-2 + ….+ аn ∙ р-n+1 – дробная часть первого произведения.
Умножив на (р) дробную часть А(рх1) первого произведения, определим вторую цифру (а2):
А(рх1) = а2 + а3 ∙ р-1 + ….+ аn ∙ р(-n+2). (2.27)
где а1 - целая часть первого произведения.
Для перевода правильной дроби из одной позиционной системы счисления в другую ее надо последовательно умножать на основание новой системы счисления (р) до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби или цифры последнего произведения должны равняться нулю.
Правильная дробь в новой системе счисления записывается из целых частей произведений, получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби.
Например: необходимо перевести из десятичной системы счисления в двоичную систему счисления правильную дробь А = 0.375(10).
Решение: исходя из вышесказанного произведем последовательное умножение А = 0.375(10) на новое основание системы счисления (2), рис.2.26:
| 0, | ||||
| Самая старшая цифра- | 0, | |||
| 1, | ||||
| 1, | ||||
| Самая младшая цифра- | 0, |
Рисунок 2.26 - Перевод из десятичной системы счисления в двоичную систему счисления правильной дроби А = 0.375(10).
Таким образом, получаем: 0, 375(10) = 0, 0110(2).
Если при переводе правильной дроби из одной позиционной системы счисления в другую при последовательном умножении на основание новой системы счисления (р) цифры последнего произведение не равняется нулю, то процесс умножения заканчивается, тогда когда появляется период и в этом случае говорят (приблизительно равно).
Правильная дробь в новой системе счисления записывается из целых частей произведений, получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби и.
Например: необходимо перевести из десятичной системы счисления в двоичную систему счисления правильную дробь А = 0.35(10).
Решение: исходя из вышесказанного произведем последовательное умножение А = 0.35(10) на новое основание системы счисления (2), рис.2.27:
| 0, | |||
| Самая старшая цифра- | 0, | ||
| 1, | |||
| 0, | |||
| 1, | |||
| 1, | |||
| Самая младшая цифра- | 0, |
Рисунок 2.27 - Перевод из десятичной системы счисления в двоичную систему счисления правильной дроби А = 0.35(10).
последнее произведение получилось равным (0, 40), а ранее было уже получено произведение (1, 40), следовательно считаем, что начался период.
Таким образом, получаем: 0, 35(10) 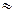 0, 010110(2).
0, 010110(2).
Например: необходимо перевести из двоичной системы счисления в десятичную систему счисления правильную дробь А = 0.0110(2).
Решение: в этом случае для преобразования чисел необходимо воспользоваться формулой (2.6). Запишем число (А) в виде суммы произведений степеней основания на соответствующую цифру в десятичной системе счисления:
А = 0.0110(2) = 0∙ 2-1+1∙ 2-2+1∙ 2-3+0∙ 2-4 = 0∙ (1/2)+1∙ (1/4)+ 1∙ (1/8)+ 0∙ (1/16) = (1/4)+(1/8) = (2/8)+(1/8) = (3/8) = 0.375(10).
Таким образом, получаем: 0.0110(2) = 0.375(10).
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Например: необходимо перевести из десятичной системы счисления в двоичную систему счисления неправильную дробь А = 23.125(10).
Решение: исходя из вышесказанного необходимо сначала перевести целую часть числа (А) путем последовательного деления на основание новой системы счисления (2) до тех пор, пока не получится частное, у которого целая часть равна (0). При этом число в новой системе счисления записывается из остатков от последовательного деления, причем последний остаток будет старшей цифрой нового числа. А затем перевести дробную часть путем последовательного умножения на основание новой системы счисления (2) до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Тогда дробная часть числа (А) в новой системе счисления записывается из целых частей произведений, получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби, рис.2.28:
| 0, | |||||||||
| 0, | |||||||||
| 0, | |||||||||
| 1, |
Рисунок 2.28 - Перевод из десятичной системы счисления в двоичную систему счисления неправильной дроби А = 23.125(10).
Таким образом, получаем: 23.125(10) - 10111.001(2).
2.3 Перевод неправильной восьмеричной (шестнадцатеричной) дроби в двоичную систему счисления
Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру исходного числа записать в виде эквивалентного ей трехбитного (четырехбитного) двоичного числа.
Например: необходимо перевести из восьмеричной системы счисления в двоичную систему счисления неправильную дробь А = 273.5(8).
Решение: исходя из вышесказанного разобьем каждую цифру неправильной восьмеричной дроби на триады и переведем каждую цифру отдельно:
| 273.5(8) = | 0 1 0 | 1 1 1 | 0 1 1, | 1 0 1(2) | = 010111011, 101(2) или 10111011, 101(2) |
| веса: | 4-2-1 | 4-2-1 | 4-2-1 | 4-2-1 |
Например: необходимо перевести из шестнадцатеричной системы счисления в двоичную систему счисления неправильную дробь А = 5АЕ.18(16).
Решение: исходя из вышесказанного разобьем каждую цифру неправильной шестнадцатеричной дроби на тетрады и переведем каждую цифру отдельно:
| 5АЕ.18(16)= | 0 1 0 1 | 1 0 1 0 | 1 1 1 0, | 0 0 0 1 | 1 0 0 0(2) | =10110101110, 00011(2) |
| веса: | 8-4-2-1 | 8-4-2-1 | 8-4-2-1 | 8-4-2-1 | 8-4-2-1 |
Лекция №6 (90-минут)