Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: выполнение арифметических операций в компьютерных системах над двоичными числами с фиксированной точкой
|
|
Подтема № 1- Операция сложения и вычитания, двоичных беззнаковых чисел в компьютерных системах
Компьютерная система выполняет сложение и вычитание операндов по правилам сложения и вычитания двоичных беззнаковых чисел рис.4.1:
| Правила сложения: | Правила вычитания: |
| 1. 0 + 0 = 0 | 1. 0 - 0 = 0 |
| 2. 0 + 1 = 1 | 2. 1 - 1 = 0 |
| 3. 1 + 0 = 1 | 3. 1 - 0 = 1 |
| 4. 1 + 1 = 10 | 4. 10 - 1 = 1 |
Рисунок 4.1 - Правила сложения и вычитания, двоичных беззнаковых чисел
Проблем не возникает до тех пор, пока значение результата не превышает разрядной сетки операнда.
Например: необходимо перевести в двоичную систему счисления, а затем сложить два числа: 7(10) и 5(10) записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел). Длина разрядной сетки операндов равна четырем битам.
Используя вышеописанные правила, мы находим сумму двух чисел следующим образом: сначала складываем числа в последнем столбце, записываем младший разряд полученной суммы под столбцом, а старший в следующий слева столбец, и продолжаем сложение, как показано на рис.4.2.
Например: необходимо перевести в двоичную систему счисления, а затем найти разность двух чисел: 9(10) и 7(10) записанных в десятичной системе счисления (по правилам вычитания двоичных беззнаковых чисел). Длина разрядной сетки операндов равна четырем битам рис.4.3.
Проблема возникает тогда, когда результат выходит за пределы разрядной сетки операнда, как показано в следующем примере.
Например: необходимо перевести в двоичную систему счисления, а затем найти сумму двух чисел: 9(10) и 7(10) записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел). Длина разрядной сетки операндов равна четырем битам рис.4.4.
| Десятичное число | Двоичное число |
| 7(10) | 0111(2) |
| 5(10) | 0101(2) |
| 12(10) | 1100(2) |
Рисунок 4.2 - Пример вычисления суммы двух чисел: 7(10) и 5(10) записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел), при четырехразрядной сетке операндов
| Десятичное число | Двоичное число |
| 9(10) | 1001(2) |
| 7(10) | 0111(2) |
| 2(10) | 0010(2) |
Рисунок 4.3 - Пример вычисления разности двух чисел: 9(10) и 7(10) записанных в десятичной системе счисления (по правилам вычитания двоичных беззнаковых чисел), при четырехразрядной сетке операндов
| Десятичное число | Двоичное число | |
| 9(10) | 1001(2) | |
| 7(10) | 0111(2) | |
| 16(10) | 0000(2) |
Рисунок 4.4 - Пример вычисления суммы двух чисел: 9(10) и 7(10) записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел), при четырехразрядной сетке операндов
В примере, представленном на рис.4.4 видно, что (1) вышла за пределы разрядной сетки операнда.
При обработке полученной суммы она не учитывается и следовательно сумма получилась равной (0), а не (16), что является не верным результатом.
В таких случаях увеличивают разрядную сетку операнда, и результат принимает правильное значение.
Например: необходимо перевести в двоичную систему счисления, а затем найти сумму двух чисел: 9(10) и 7(10) записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел). Длина разрядной сетки операндов равна восьми битам рис.4.5:
| Десятичное число | Двоичное число |
| 9(10) | 00001001(2) |
| 7(10) | 00000111(2) |
| 16(10) | 00010000(2) |
Рисунок 4.5 - Пример вычисления суммы двух чисел: 9(10) и 7(10) записанных в десятичной системе счисления (по правилам сложения двоичных беззнаковых чисел), при восьмиразрядной сетке операндов
В компьютерной системе этот исход сложения прогнозируется и предусмотрены специальные средства для фиксирования подобных ситуаций и их обработки.
Так, для фиксирования ситуации выхода за разрядную сетку результата, как в данном примере, предназначен флаг переноса (FC). Он располагается в бит - (0) регистра флагов eflags. Именно установкой этого флага фиксируется факт переноса (1) из старшего разряда операнда за пределы разрядной сетки.
Естественно, что программист должен предусматривать возможность такого исхода операции сложения и средства для корректировки. Это предполагает включение участков кода после операции сложения, в которых анализируется флаг (FC). Анализ этого флага можно провести различными способами. Самый простой и доступный использовать команду условного перехода. Эта команда в качестве операнда имеет имя метки в текущем сегменте кода. Переход на эту метку осуществляется в случае если в результате работы предыдущей команды флаг (FC) установился в (1).
Подтема № 2- Операция сложения и вычитания двоичных знаковых чисел в компьютерных системах
При сложении и вычитании знаковых двоичных чисел операция вычитания заменяется операцией сложения в дополнительном коде.
Докажем, что результат выполнения операций сложения и вычитания над числами, представленными в ДК, являются ПК, ОК или ДК соответственно.
Для этого рассмотрим отдельно формирование числовой и знаковой частей суммы.
Тогда операцию сложения проанализируем над «псевдомодулями» слагаемых - дополнительными кодами, у которых отброшен знаковый разряд.
В этом случае граничное число (C) станет равным весу знакового разряда, который становится отсутствующим.
Представим операцию сложения в общем виде:
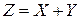. (4.1)
где Z - сумма;
X - первое слагаемое;
Y - второе слагаемое.
В зависимости от знаков слагаемых возможны следующие варианты:
1. 
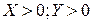, тогда:
.
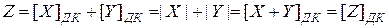Например: рассмотрим два случая а) и б).
Случай а): необходимо вычислить сумму двух чисел записанных в десятичной системе счисления (5+2=7), для этого необходимо оба числа перевести в двоичную систему счисления, а затем представить в дополнительном коде, для удобства возьмем длину разрядной сетки четыре бита. Формат суммы представлен на рис. 4.6, а вычисление суммы и значения флагов на рис.4.7.
| 0, | |||
| D3 | D2 | D1 | D0 |
Рисунок 4.6 - Формат суммы
| Случай а) | ||
| Десятичное число | Двоичное число | Значения флагов |
| 5(10) | 0, 101(2) | FC=0 |
| 2(10) | 0, 010(2) | FS=0 |
| 7(10) | 0, 111(2) | FZ=0 |
| FO=0 |
Рисунок 4.7 - Пример вычисления суммы двух чисел и значение флагов после получения результата
Значение флагов:
- FC=0, потому, что нет перехода (1) из разряда D2 в знаковый разряд D3 и нет перехода из знакового разряда D3 за пределы разрядной сетки.
- FS=0, потому, что значение знакового бита D3=0.
- FZ=0, потому, что сумма не равняется (0).
- FO=0, потому, что результат правильный и переполнение разрядной сетки нет.
Случай б): необходимо сложить два числа записанных в десятичной системе счисления (7+7=14), для этого необходимо оба числа перевести в двоичную систему счисления, а затем представить в дополнительном коде, для удобства возьмем длину разрядной сетки четыре бита.
Формат суммы представлен на рис. 4.8, а вычисление суммы и значения флагов на рис.4.9.
| 1, | |||
| D3 | D2 | D1 | D0 |
Рисунок 4.8 - Формат суммы
| Случай б) | ||
| Десятичное число | Двоичное число | Значения флагов |
| 7(10) | 0, 111(2) | FC=1 |
| 7(10) | 0, 111(2) | FS=1 |
| 14(10) | 1, 110(2) | FZ=0 |
| FO=1 |
Рисунок 4.9 - Пример вычисления суммы двух чисел и значение флагов после получения результата
Значение флагов:
- FC=1, потому, что есть перехода (1) из разряда D2 в знаковый разряд D3 и нет перехода из знакового разряда D3 за пределы разрядной сетки.
- FS=1, потому, что значение знакового бита D3=1, а это не правильно так как оба слагаемых положительные числа, значит и сумма должна быть положительной, а в данном случае сумма получается отрицательной так как знаковый бит равен (1).
- FZ=0, потому, что сумма не равняется (0).
- FO=1, потому, что результат не правильный и переполнение разрядной сетки есть.
2. 
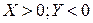и 
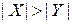, тогда:
.
Например: необходимо сложить два числа записанных в десятичной системе счисления (5+(-2)=3), для этого необходимо оба числа перевести в двоичную систему счисления, а затем представить в дополнительном коде, для удобства возьмем длину разрядной сетки четыре бита.
Формат суммы представлен на рис. 4.10, а вычисление суммы и значения флагов на рис.4.11.
| 0, | ||||
| D3 | D2 | D1 | D0 |
Рисунок 4.10 - Формат суммы
| Десятичное число | Двоичное число | Значения флагов |
| 5(10) | 0, 101(2) | FC=0 |
| (-2)(10) | 1, 110(2) | FS=0 |
| (3)(10) | 10, 011(2) | FZ=0 |
| FO=0 |
Рисунок 4.11 - Пример вычисления суммы двух чисел и значение флагов после получения результата
Значение флагов:
- FC=0, потому, что есть перехода (1) из разряда D2 в знаковый разряд D3 и есть перехода из знакового разряда D3 за пределы разрядной сетки.
- FS=0, потому, что значение знакового бита D3=0.
- FZ=0, потому, что сумма не равняется (0).
- FO=0, потому, что результат правильный и переполнение разрядной сетки нет. Единица, которая вышла за пределы разрядной сетки не учитывается.
3. 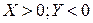и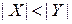 
, тогда: 
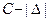, по сути, представляет собой дополнительный код отрицательной разности:
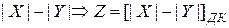. так как
.
Например: необходимо сложить два числа записанных в десятичной системе счисления (2+(-5)=(-3)), для этого необходимо оба числа перевести в двоичную систему счисления, а затем представить в дополнительном коде, для удобства возьмем длину разрядной сетки четыре бита.
Формат суммы представлен на рис. 4.12,, а вычисление суммы и значения флагов на рис.4.13.
| 0, | ||||
| D3 | D2 | D1 | D0 |
Рисунок 4.12 - Формат суммы
| Десятичное число | Двоичное число | Значения флагов |
| 2(10) | 0, 010(2) | FC=0 |
| (-5)(10) | 1, 011(2) | FS=1 |
| (-3)(10) | 1, 101(2) | FZ=0 |
| FO=0 |
Рисунок 4.13 - Пример вычисления суммы двух чисел и значение флагов после получения результата
Значение флагов:
- FC=0, потому, что нет перехода (1) из разряда D2 в знаковый разряд D3 и нет перехода из знакового разряда D3 за пределы разрядной сетки.
- FS=1, потому, что значение знакового бита D3=1.
- FZ=0, потому, что сумма не равняется (0).
- FO=0, потому, что результат правильный и переполнение разрядной сетки нет. Число 1, 101 и есть (-3). Для того, чтобы перейти к прямому коду необходимо все биты проинвертировать, а затем к младшему биту прибавить (1), рис.4.14:
| 1, 101(2) | (-3) |
| 0, 010(2) | инверсия |
| 1(2) | +1 |
| 0, 011(2) | (+3) |
Рисунок 4.14 - Пример перехода от дополнительного кода числа к прямому коду
4. 
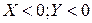, тогда:
.
Например: рассмотрим два случая а) и б).
Случай а): необходимо сложить два числа записанных в десятичной системе счисления ((-5)+(-2)=(-7)), для этого необходимо оба числа перевести в двоичную систему счисления, а затем представить в дополнительном коде, для удобства возьмем длину разрядной сетки четыре бита. Формат суммы представлен на рис. 4.15, а вычисление суммы и значения флагов на рис.4.16.
| 1, | ||||
| D3 | D2 | D1 | D0 |
Рисунок 4.15 - Формат суммы
| Случай а) | ||
| Десятичное число | Двоичное число | Значения флагов |
| (-5)(10) | 1, 011(2) | FC=0 |
| (-2)(10) | 1, 110(2) | FS=1 |
| (-7)(10) | 11, 001(2) | FZ=0 |
| FO=0 |
Рисунок 4.16 - Пример вычисления суммы двух чисел и значение флагов после получения результата
Значение флагов:
- FC=0, потому, что есть переход (1) из разряда D2 в знаковый разряд D3 и есть перехода из знакового разряда D3 за пределы разрядной сетки.
- FS=1, потому, что значение знакового бита D3=1.
- FZ=0, потому, что сумма не равняется (0).
- FO=0, потому, что результат правильный и переполнение разрядной сетки нет. Единица, которая вышла за пределы разрядной сетки не учитывается.
Число 1, 001 и есть (-7). Для того, чтобы перейти к прямому коду необходимо все биты проинвертировать, а затем к младшему биту прибавить (1), рис.4.17. Случай б): необходимо сложить два числа записанных в десятичной системе счисления ((-7)+(-7)=(-14)), для этого необходимо оба числа перевести в двоичную систему счисления, а затем представить в дополнительном коде, для удобства возьмем длину разрядной сетки четыре бита.
Формат суммы представлен на рис. 4.18, а вычисление суммы и значения флагов на рис.4.19.
| 1, 001(2) | (-7) |
| 0, 110(2) | инверсия |
| 1(2) | +1 |
| 0, 111(2) | (+7) |
Рисунок 4.17 - Пример перехода от дополнительного кода числа к прямому коду
| 0, | ||||
| D3 | D2 | D1 | D0 |
Рисунок 4.18 - Формат суммы
| Случай б) | ||
| Десятичное число | Двоичное число | Значения флагов |
| (-7)(10) | 1, 001(2) | FC=1 |
| (-7)(10) | 1, 001(2) | FS=0 |
| (-14)(10) | 10, 010(2) | FZ=0 |
| FO=1 |
Рисунок 4.19 - Пример вычисления суммы двух чисел и значение флагов после получения результата
Значение флагов:
- FC=1, потому, что нет перехода (1) из разряда D2 в знаковый разряд D3 и есть переход из знакового разряда D3 за пределы разрядной сетки.
- FS=0, потому, что значение знакового бита D3=0, а это не правильно так как оба слагаемых отрицательные числа, значит и сумма должна быть отрицательные, а в данном случае сумма получается положительной так как знаковый бит равен (0).
- FZ=0, потому, что сумма не равняется (0).
- FO=1, потому, что результат не правильный и переполнение разрядной сетки есть. Единица, которая вышла за пределы разрядной сетки не учитывается.
Из вышесказанного на примере (4х- разрядной) сетки можно сделать следующие выводы:
- переполнение разрядной сетки возможно, когда оба операнда имеют одинаковые знаки;
- есть переход (1) из разряда D2 в знаковый разряд D3 и нет перехода из знакового разряда D3 за пределы разрядной сетки.
- нет перехода (1) из разряда D2 в знаковый разряд D3 и есть переход из знакового разряда D3 за пределы разрядной сетки.
При возникновении ситуации переполнения, увеличивается количество бит в разрядной сетке и результат становится правильным.
4.3 Операции сдвига в компьютерных системах
Является одной из самых распространенных в компьютерной арифметике. В частности, она используется при выполнении умножения или деления двоичных чисел. Обычно выполняется в регистрах как встроенная микрооперация за счет специальной организации внутрирегистровых связей.
Существует несколько вариантов сдвига:
1. Логический сдвиг. Сдвиг, который выполняется над всеми разрядами операнда, включая знаковый.
2. Арифметический сдвиг. Не влияет на положение знака операнда.
Арифметический сдвиг двоичного операнда влево или вправо на (i) разрядов эквивалентно соответственно умножению и делению исходного операнда на (2i). При сдвиге вправо разряды исходного операнда, которые выходят за пределы разрядной сетки регистра, теряются, внося при этом ошибку, которая по абсолютной величине не превышает полученного после сдвига числа. Сдвиг влево имеет смысл, пока не теряются значащие цифры операнда.
3. Модифицированный сдвиг. Арифметический сдвиг операндов, представленных обратным или дополнительным кодом:
- обратный код - при правом и левом сдвигах в освобождающиеся разряды регистра записываются цифры знакового разряда;
- дополнительный код - при сдвиге вправо в разряды, которые освобождаются, записываются цифры знакового разряда, а при сдвиге влево в освобождающиеся разряды записываются нули.
4. Циклический сдвиг. Операнд перемещается в регистре как в замкнутом контуре, поступая с выхода последнего разряда на вход первого.
Схемы выполнения операций сдвига приведены на рис. 4.20.
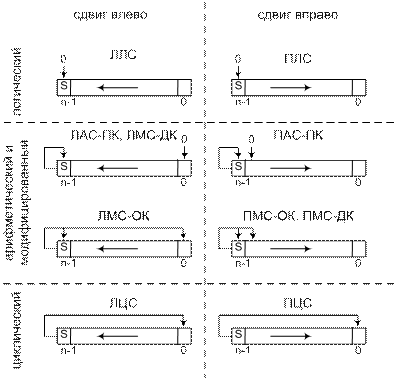
Рисунок 4.20 - Схемы выполнения операций сдвига
Лекция № 9 (90-минут)