Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способ №2
|
|
| Десятичное число | Двоичное число | Комментарии |
| 7(10) | 0111(2) | множимое |
| 3(10) | 0011(2) | множитель |
| номера цифр множителя | ||
| 1ое – ЧП | ||
| 2ое – ЧП | ||
| 3ое – ЧП | ||
| 4ое – ЧП | ||
| 21(10) 0010101(2) | сумма ЧП - произведение | |
Рисунок 4.22 - Умножение, начиная со старшей цифры множителя и сдвиг частичных произведений вправо.
В отличие от ручного умножения, операционное устройство компьютера не может просуммировать сразу (s) частичных произведений, как это делает человек. Обычный сумматор, как правило, рассчитан на одновременное сложение только двух операндов. Если нужно получить сумму нескольких слагаемых, то происходит накопление суммы: сначала в сумматор записывается первое слагаемое, к нему прибавляется второе, затем к полученной сумме прибавляется третье слагаемое и так до получения полной суммы.
Длина произведения s-битных сомножителей равна 2s бит:
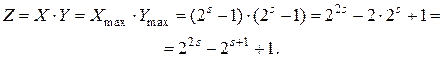(4.5)
Поскольку умножение на (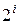
) эквивалентно сдвигу влево, то вычисление произведения (Z) сводится к формированию частичных произведений (
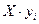), их сдвигу и суммированию с учетом весов, определяемых величинами (
).
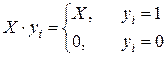(4.6)
Умножение реализуется циклическим процессом, на каждом шаге которого:
- анализируется очередной бит (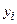
) множителя;
- в зависимости от его значения происходит (yi=1) или нет (yi=0) прибавление множимого к предыдущей сумме частичных произведений;
- производится изменение взаимного положения множимого (X) и суммы частичных произведений с учетом веса (2i).
Таким образом, умножение в двоичной системе счисления естественным образом сводится к двум операциям - сложению и сдвигу чисел.
В соответствии со способом формирования суммы частичных произведений - (ЧП), возможны четыре варианта умножения. Они различаются тем, с каких разрядов множителя (Y) (младших или старших) начинается умножение, и что сдвигается (множимое или сумма ЧП).
Варианты умножения, начиная с младших или старших разрядов множителя, называются еще умножением младшими и старшими разрядами вперед соответственно.
Схемы выполнения операции умножения двоичных беззнаковых чисел представлены на рис. 4.23.
При умножении младшими разрядами вперед производятся последовательные сдвиги множителя вправо, вследствие чего в младшем разряде регистра множителя последовательно появляются все его цифры, начиная с младшей. Т.о., в специальной схеме анализа значения текущей цифры множителя нужно анализировать только состояние младшего разряда соответствующего регистра.
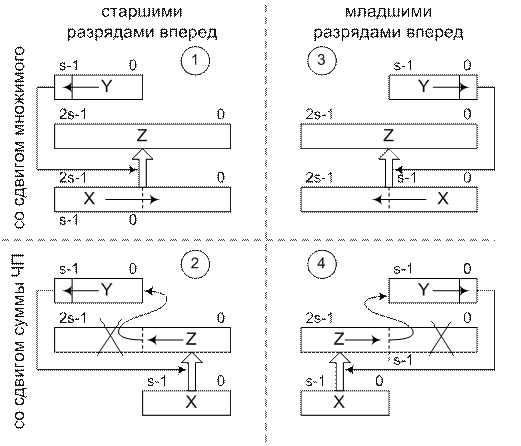
Рисунок 4.23 - Схемы выполнения операции умножения двоичных беззнаковых чисел
Соответственно, при умножении старшими разрядами вперед должен анализироваться старший разряд множителя.