
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: Деление двоичных беззнаковых чисел в компьютерных системах
|
|
Деление мантисс чисел в форме с фиксированной запятой выполняется над абсолютными величинами операндов, представленными, чаще всего, прямым кодом.
Подобно умножению, деление в компьютерных системах реализуется как многошаговый процесс выполнения операций суммирования, сдвига и других элементарных операций.
В отличие от умножения этот процесс имеет итеративный характер, так как результат деления в большинстве случаев не может быть точно представлен числом конечной длины.
Как правило, формальным признаком окончания операции деления принимается количество сдвигов: при достижении числа сдвигов, равного количеству разрядов в частном, операция деления завершается.
Обозначим X - делимое, Y - делитель, а Z - частное. Тогда:
 . (4.19)
. (4.19)
Пусть (X), (Y) и (Z) являются беззнаковыми числами.
Операция деления характеризуется также дополнительным результатом (R) - остатком.
В практической реализации выделяют два типа операции деления:
- первый тип это когда делимое, делитель и частное имеют одну и ту же длину (s);
- второй тип это когда делимое имеет длину (2s) - удвоенную по сравнению с делителем и частным. Рассмотрим случай 1.
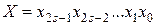 ,
, 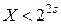 . (4.20)
. (4.20)
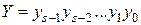 ,
, 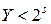 . (4.21)
. (4.21)
 ,
, 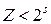 . (4.22)
. (4.22)
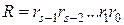 ,
, 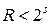 . (4.23)
. (4.23)
 . (4.24)
. (4.24)
Для того, чтобы деление было корректным, т.е. чтобы частное не превысило разрядную сетку, необходимо обеспечить выполнение условия:
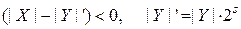 . (4.25)
. (4.25)
или
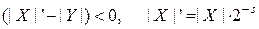 . (4.26)
. (4.26)
В противном случае будет иметь место переполнение разрядной сетки.
Переполнение исключено, если делимое и делитель имеют одинаковую длину. Как особый случай переполнения рассматривают попытку деления на нуль.
По существу, деление сводится к последовательности вычитаний делителя вначале из делимого, а затем из остатков.
Цифра (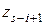 ) частного определяется следующим образом: если текущий остаток (
) частного определяется следующим образом: если текущий остаток ( ) больше или равен делителю, цифра частного равна (1), если меньше, то цифра частного равна (0).
) больше или равен делителю, цифра частного равна (1), если меньше, то цифра частного равна (0).
При этом операция сравнения реализуется посредством операции вычитания.
Так как частное можно определить только со старших разрядов, существует два варианта деления представленных на рис. 4.9:
- с неподвижным делимым (частичным остатком) и сдвигаемым вправо делителем;
- с неподвижным делителем и сдвигаемым влево делимым (частичным остатком).
В зависимости от способа обработки отрицательного частичного остатка, различают два алгоритма деления:
- алгоритм №1, с восстановлением остатка;
- алгоритм №2 без восстановления остатка.
Деление с восстановлением остатка заключается в следующем, если на очередном шаге получен положительный остаток, то в очередную цифру частного записывается (1), а остаток становится «предыдущим» для следующего шага.
Данный шаг на этом заканчивается.
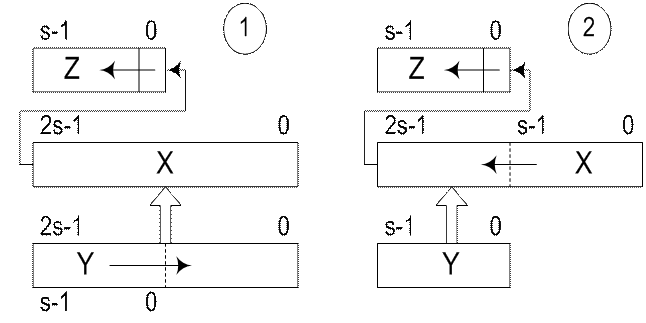
Рисунок 4.9 - Схемы деления двоичных беззнаковых чисел
Если текущий остаток отрицателен, то в очередную цифру частного записывается (0), а к остатку прибавляется делитель для восстановления предыдущего, сдвинутого влево остатка, который становится «предыдущим» для следующего шага.
Таким образом, отрицательный остаток аннулируется, поскольку он выполнил свою функцию сигнализатора о соотношении модулей остатка и делителя и больше не нужен.
Алгоритм №1. Деление целых двоичных беззнаковых чисел методом с восстановлением остатка.
1. Исходное значение частного (Z) полагается равным (0). (Сч.Т) присваивается значение (s). Исходное значение частичного остатка (R0) полагается равным (s) старшим разрядам делимого.
2. Выполняется пробное вычитание делителя (Y) из исходного значения частичного остатка – (ЧО). Положительная разность указывает на то, что частное превысит (s-разрядную сетку), и будет выполнено прерывание. Если же результат вычитания отрицательный, то деление можно выполнять.
3. Восстанавливается исходное значение (ЧО) прибавлением делителя к полученному отрицательному остатку.
4. (ЧО) удваивается путем сдвига на один разряд влево.
5. Из (ЧО) вычитается делитель и анализируется знак результата вычитания: если остаток положительный, то очередная цифра частного равна (1), иначе – (0).
6. Частное сдвигается влево с занесением очередной полученной цифры частного в освободившийся младший разряд. (Сч.Т) уменьшается на (1).
7. Если полученный остаток отрицателен, то восстанавливается предыдущий положительный остаток прибавлением делителя к отрицательному остатку.
8. (Пп. 4-7) последовательно выполняются до получения всех цифр частного, пока (Сч.Т) не станет равным (0).
9. Если последний остаток от деления отрицателен, то восстанавливается предыдущий положительный остаток, который будет окончательным остатком от деления.
Недостатки:
- нерегулярность выполнения операций, что усложняет устройство управления (для получения одной цифры частного необходимо выполнять либо одно вычитание и сдвиг, либо одно вычитание, одно сложение и сдвиг);
- относительно малая скорость деления, т.к. в среднем половина шагов будет содержать операцию восстановления остатка.
T=(s+l)(l, 5t++tc)–tc.
Например: необходимо разделить два беззнаковых числа (21: 7=3).
Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
Х = 21 – делимое;
Y = 7 – делитель;
Z = 3 – частное.
Если (Z) и (Y) равняется четырем битам, то как было отмечено выше (X) должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного.
Алгоритм деления приведен в табл. 4.3.
Таблица 4.3 - Алгоритм деление целых двоичных беззнаковых чисел методом с восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| < 0 | ||||||||||||||||||||
| < 0 | ||||||||||||||||||||
| < 0 | ||||||||||||||||||||
| > 0 | ||||||||||||||||||||
| > 0 | ||||||||||||||||||||
| СТОП | ||||||||||||||||||||
Деления без восстановления остатка заключается в следующем, исходной предпосылкой для использования данного метода является желание избавиться от процедуры восстановления остатка.
Благодаря этому, длительность деления можно существенно уменьшить по сравнению с вышеприведенной оценкой (за счет исключения " лишней" операции восстановления остатка), используя алгоритм деления без восстановления остатка.
Проанализируем шаг деления, при котором текущий остаток оказался отрицательным. Обозначим:
- ( ) - предыдущий остаток;
) - предыдущий остаток;
- ( ) - текущий;
) - текущий;
- (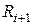 ) - последующий.
) - последующий.
Пусть:
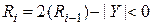 . (4.27)
. (4.27)
При этом, в соответствии с правилом деления, должны выполняться три действия:
- восстановление предыдущего (сдвинутого влево) остатка:
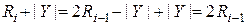 . (4.28)
. (4.28)
- сдвиг восстановленного остатка влево на один разряд:
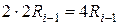 . (4.29)
. (4.29)
- вычитание модуля делителя из полученной кодовой комбинации:
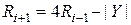 . (4.30)
. (4.30)
Таким образом, требуется перейти от текущего остатка:
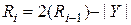 . (4.31)
. (4.31)
к последующему виду (4.31), избавившись от операции восстановления.
Если первым действием является сдвиг отрицательного остатка ( ) влево, то:
) влево, то:
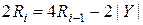 . (4.32)
. (4.32)
Правая часть (4.32) отличается от требуемого вида величиной |Y|.
Поэтому вторым действием будет корректировка (4.33):
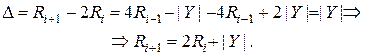 . (4.33)
. (4.33)
Сформулируем общее правило.
Чтобы определить цифру частного в некотором разряде, необходимо сдвинуть логически ( ) влево на один разряд, а затем прибавить к нему код делителя, которому приписывается знак, противоположный знаку предыдущего остатка; если полученный (
) влево на один разряд, а затем прибавить к нему код делителя, которому приписывается знак, противоположный знаку предыдущего остатка; если полученный ( ) положительный, то в частном проставляется (1), если же отрицательный, - то (0).
) положительный, то в частном проставляется (1), если же отрицательный, - то (0).
Алгоритм №2. Деления целых двоичных чисел методом без восстановления остатка
1-2. Аналогично п.п. 1, 2 предыдущего.
3. Аналогично п. 4.
4. Из частичного остатка вычитается делитель, если остаток положительный, или к частичному остатку прибавляется делитель, если остаток отрицательный.
5. Частное сдвигается; в младший разряд заносится очередная цифра частного (1 — при положительном остатке, 0 — при отрицательном);
6. П.п. 3-5 последовательно выполняются для получения всех цифр частного, пока (Сч.Т) не станет равен (0).
7. Аналогично последнему пункту предыдущего алгоритма.
Реализация данного алгоритма не требует никаких дополнительных аппаратурных затрат.  .
.
Например: необходимо разделить два беззнаковых числа (21: 7=3).
Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
Х = 21 – делимое;
Y = 7 – делитель;
Z = 3 – частное.
Если (Z) и (Y) равняется четырем битам, то как было отмечено выше (X) должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного.
Алгоритм деления приведен в табл. 4.4.
Таблица 4.4 - Алгоритм деление целых двоичных беззнаковых чисел методом без восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| < 0 | ||||||||||||||||||||
| < 0 | ||||||||||||||||||||
| < 0 | ||||||||||||||||||||
| > 0 | ||||||||||||||||||||
| > 0 | ||||||||||||||||||||
| СТОП | ||||||||||||||||||||
Лекция № 11 (90-минут)