Для решения необходимо сделать это уравнение с разделенными переменными

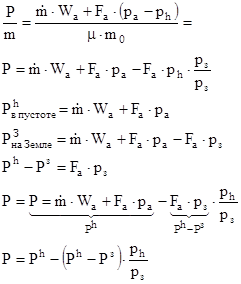
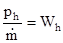- эффективная скорость истечения продуктов сгорания из сопла двигателя в пустоте. Она всегда больше истинной или реальной.

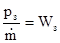- эффективная скорость истечения продуктов сгорания из сопла двигателя на Земле.

Она равна истинной, когда р_а=р_з.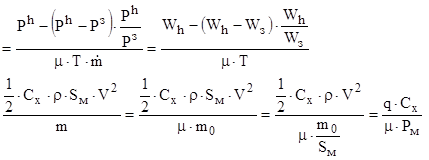

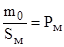-стартовая нагрузка на мидель ракеты, величина постоянная для данной ракеты,

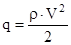- скоростной напор.

Таким образом уравнение (3) будет иметь следующий вид:

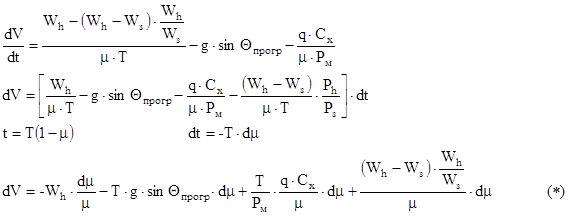
Полученное уравнение (*) решается методом последовательных приближений. В первом приближении учитываются только первые два слагаемых, двумя последними принебрегаем. Проинтегрируем уравнение (*)

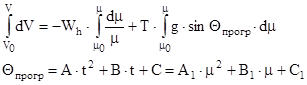
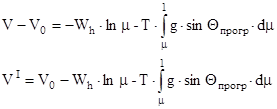
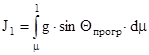- первый интеграл Королева;

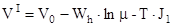- скорость ракеты в первом приближении.

В первом приближении определяем только высоту полета. Для этого запишем уравнение 2.

→

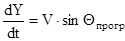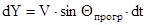
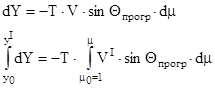
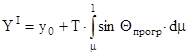- высота полета в первом приближении.

Таким образом скорость полета ракеты в первом приближении равна идеальной скорости минус потери скорости на преодоление силы тяжести.

При вычислении скорости во втором приближении необходимо учитывать влияние атмосферы и противодавление на срезе сопла двигателя.

Тогда формула (*) будет иметь вид:

После интегрирования уравнения (**) получаем:

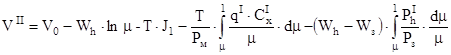, где

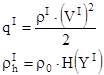
Посчитанный q близок к истинному q на траектории полета ракеты, т.к. он определяется по завышенной скорости и заниженной плотности.

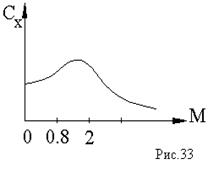
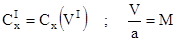
Для реальных скоростей этот промежуток (0.8...2.0) небольшой по времени, а значит, принимая величину С_х мы не делаем грубых ошибок.

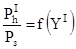- эта величина в общем случае занижена, т.к. определяется по завышенной высоте.

Но сама величина третьего интеграла незначительна, поэтому эта неточность не оказывает существенного влияния на величину скорости.

Принято обозначать:

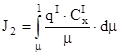- второй интеграл Королева.

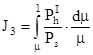- третий интеграл Королева.

Таким образом получается:

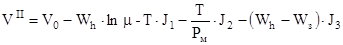- формула скорости ракеты во втором и окончательном приближении.

Зная скорость можно найти высоту и дальность.

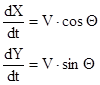
После всех преобразований получим:

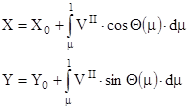
- формулы для определения высоты и дальности во втором приближении.

Рассмотрим выполнение программного угла Θ.

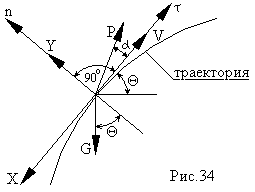Для того, чтобы определить, как меняется угол Θ составим дифференциальное уравнение движения ракеты в проекции на ось n.

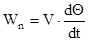- ускорение движения в проекции на ось n.

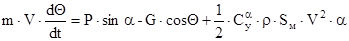
Решая это уравнение совместно с уравнением скорости, высоты и дальности мы получим величину Θ, как функцию времени. С другой стороны для того, чтобы ракета выполнила программу угол Θ =Θ _прогр.

Выполнение угла Θ _прогр обеспечивается выполнением вполне определенного угла атаки α, т.е. α =α _пргр=α (t).