Частные случаи .

Рассмотрим несколько случаев:

1. Плоскость перпендикулярна оси конуса.

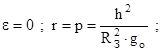
В сечении будет окружность, следовательно точка движется по окружности.

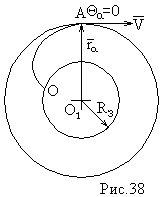
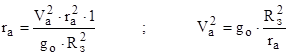
Необходимая скорость, которую должна получить ракета в точке А, чтобы она могла двигаться по орбите вокруг Земли, эту скорость принято называть первой космической скоростью.

.

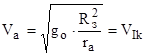2.

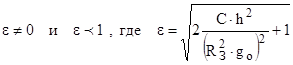
Это уравнение эллипса или эллиптическая траектория. В этом случае С< 0. Для этого случая запишем уравнение энергии:

- необходимое условие для получения эллипса.

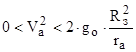- траектория эллипса.

Случаи:

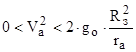§ - эллиптическая траектория ракеты класса “Земля – Земля” (рис.39).

§ - это орбитальный эллипс и его вытянутость зависит от величины скорости в точке А (рис.40).

3.

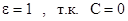
Уравнение энергии

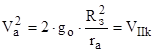- вторая космическая скорость.

Приближенно можно считать, что V_Ik≈ 8 км/с, а V_IIk≈ 11.2 км/с.

4. 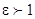- это траектория гиперболы при С> 0.

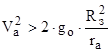- гиперболическая скорость (третья космическая скорость).

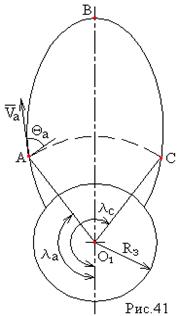Время полета ракеты на эллиптической траектории.

Уравнение траектории движения ракеты на эллиптическом участке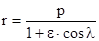

Запишем уравнение для момента количества движения точки единичной массы: