
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Teopeмa сложения скоростей.
|
|
Пусть некоторая точка М совершает движение по отношению к системе отсчета Oxyz, которая сама движется произвольным образом по отношению к неподвижной системе отсчета 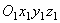 , (рис.49).
, (рис.49).
Конечно, абсолютное движение точки М определяется уравнениями
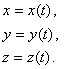
Относительное движение – в движущихся осях уравнениями
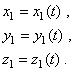
|
Уравнений, определяющих переносное движение точки, не может быть вообще. Так как, по определению, переносное движение точки М – это движение относительно неподвижных осей той точки системы 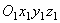 , с которой совпадает точка в данный момент. Но все точки подвижной системы движутся по-разному.
, с которой совпадает точка в данный момент. Но все точки подвижной системы движутся по-разному.
Положение подвижной системы отсчета может быть также определено, если задать положение точки О радиусом-вектором 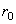 , проведенным из начала неподвижной системы отсчета, и направления единичных векторов
, проведенным из начала неподвижной системы отсчета, и направления единичных векторов 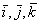 подвижных осей Оx, Oy, Oz.
подвижных осей Оx, Oy, Oz.
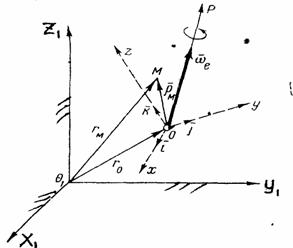
Рис.49
Произвольное переносное движение подвижной системы отсчета слагается из поступательного движения со скоростью 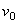 точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью
точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью 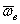 . Вследствие переносного движения подвижной системы отсчета радиус-вектора
. Вследствие переносного движения подвижной системы отсчета радиус-вектора 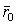 и направления единичных векторов
и направления единичных векторов 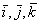 изменяются. Если векторы
изменяются. Если векторы 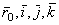 заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.
заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.
Положение точки М по отношению к подвижной системе отсчета можно определить радиусом-вектором 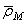
 ,
,
где координаты x, y, z точки М изменяются с течением времени вследствие движения точки М относительно подвижной системы отсчета. Если радиус-вектор  задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.
задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.
Положение точки М относительно неподвижной системы отсчета 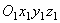 , может быть определено радиусом-вектором
, может быть определено радиусом-вектором 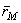 . Из рис.49 видно, что
. Из рис.49 видно, что
 . (1)
. (1)
Если относительные координаты x, y, z точки М и векторы 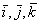 определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.
определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.
Скорость составного движения точки М, или абсолютная скорость этой точки, равна, очевидно, производной от радиуса-вектора 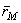 точки M по времени t
точки M по времени t
 .
.
Поэтому, дифференцируя равенство (1) по времени t, получим
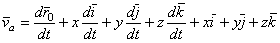 . (2)
. (2)
Разобьем слагаемые в правой части этого равенства на две группы по следующему признаку. К первой группе отнесем те слагаемые, которые содержат производные только от относительных координат x, y, z, а ко второй - те слагаемые, которые содержат производные от векторов 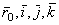 , т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета
, т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета
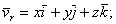 (3)
(3)
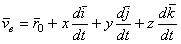 . (4)
. (4)
Каждая из групп слагаемых, обозначенных через 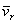 и
и  , представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоростей
, представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоростей 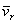 и
и  .
.
Скорость 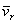 , как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x, y, z точки М, но векторы
, как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x, y, z точки М, но векторы 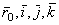 остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость
остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость 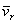 представляет собой относительную скорость точки М.
представляет собой относительную скорость точки М.
Скорость  вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x, y, z в равенство (4) не входят. Поэтому скорость
вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x, y, z в равенство (4) не входят. Поэтому скорость  представляет собой переносную скорость точки М.
представляет собой переносную скорость точки М.
Итак, 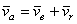 . (5)
. (5)
Это равенство выражает теорему сложения скоростей в случае, когда переносное движение является произвольным: абсолютная скорость точки М равна геометрической сумме переносной и относительной скоростей этой точки.
Пример 13. Колечко М движется по вращающемуся стержню так, что  (см) и
(см) и 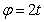 (рад).
(рад).

Рис.50
Ранее было установлено, что траектория относительного движения – прямая линия, совпадающая со стержнем, и движение это определяется уравнением 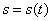 . Траектория переносного движения точки М в момент времени t – окружность радиуса
. Траектория переносного движения точки М в момент времени t – окружность радиуса 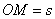 .
.
Поэтому относительная скорость 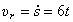
 . И направлена по касательной к траектории вдоль стержня (рис.50). Переносная скорость колечка, как при вращении вокруг оси,
. И направлена по касательной к траектории вдоль стержня (рис.50). Переносная скорость колечка, как при вращении вокруг оси, 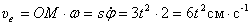 . Направлен вектор этой скорости по касательной к траектории переносного движения, перпендикулярно стержню.
. Направлен вектор этой скорости по касательной к траектории переносного движения, перпендикулярно стержню.
Абсолютная скорость колечка 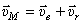 . Величина ее, т.к.
. Величина ее, т.к. 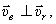
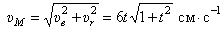 .
.