Теорема сложения ускорений. Ускорение Кориолиса.

Ускорение составного движения точки М, или абсолютное ускорение этой точки, равно, очевидно, производной от абсолютной скорости точки М по времени t

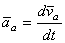
Поэтому, дифференцируя равенство по времени, получим

.

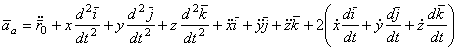Разделим слагаемые правой части этого равенства на три группы.

К первой группе отнесем слагаемые, содержащие только производные от относительных координат x, y и z, но не содержащие производные от векторов :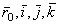

.

Ко второй группе отнесем слагаемые, которые содержат только производные от векторов 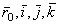, но не содержащие производных от относительных координат x, y, z:

.

Осталась еще одна группа слагаемых, которые не могли быть отнесены ни к первой, ни ко второй, так как они содержат производные от всех переменных x, y, z, 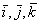. Обозначим эту группу слагаемыхчерез :

.

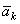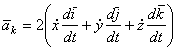Каждая из выделенных групп представляет собой, по крайней мере по размерности, некоторое ускорение. Выясним физический смысл всех трех ускорений: .

Ускорение 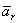, как это видно из равенства, вычисляется так, как если бы относительные координаты x, y, z изменялись с течением времени, а векторы 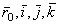оставались неизменными, т.е. подвижная система отсчета Oxyz как бы покоилась, а точка М двигалась. Поэтому ускорение 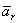представляет собой относительное ускорение точки М. Так как ускорение (и скорость) относительного движения вычисляется в предположении, что подвижная система отсчета находится а покое, то для определения относительного ускорения (и скорости) можно пользоваться всеми правилами, изложенными ранее в кинематике точки.

Ускорение 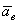, как это видно из равенства, вычисляется в предположении, что сама точка М покоится по отношению к подвижной системе отсчета Oxyz (x =const, y =const, z =const) и перемещается вместе с этой системой отсчета по отношению к неподвижной системе отсчета 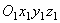. Поэтому ускорение 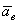представляет собой переносное ускорение точки М.

Третья группа слагаемых определяет ускорение 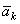, которое не может быть отнесено не к относительному ускорению 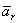, так как содержит в своем выражении производные 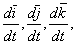не к переносному ускорению 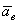, так как содержит в своем выражении производные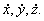

Преобразуем правую часть равенства, припомнив, что

Подставляя эти значения производных в равенства, получим

или .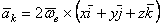

Здесь вектор есть относительная скорость 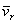точки М, поэтому

.

Ускорение 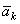называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.

С физической точки зрения появление поворотного ускорения точки объясняется взаимным влиянием переносного и относительного движений.

Итак, ускорение Кориолиса точки равно по модулю и направлению удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.

Равенство, которое теперь можно сокращенно записать в виде

.

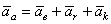представляет теорему сложения ускорений в случае, когда переносное движение является произвольным: абсолютное ускорение точки равно векторной сумме переносного, относительного и поворотного ускоре­ний. Эту теорему часто называют теоремой Кориолиса.

Из формулы следует, что модуль поворотного ускорения будет

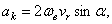
где 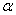- угол между вектором 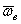и вектором 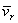. Чтобы определить направление поворотного ускорения 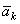, нужно мысленно перенести вектор 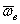в точку М и руководствоваться правилом векторной алгебры. Согласно этому правилу, вектор 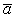нужно направлять перпендикуляр­но к плоскости, определяемой векторам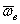и и 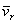, и так, чтобы, смотря с конца вектора 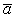, наблюдатель мог видеть кратчайший поворот от 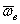к 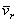происходящим против движения часовой стрелки (рис. 30).

Для определения направления 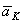можно также пользоваться следующим правилом Н. Е. Жу­ковского: чтобы получить направление поворот­ного ускорения 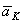, достаточно составляющую 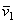относительной скорости 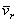точки М, перпенди­кулярную к вектору 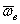, повернуть (в плоскости, перпендикулярной к вектору 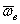) на прямой угол вокруг точки М в направлении переносного вра­щения (рис.51).

Рис.51

Если переносное движение подвижной систе­мы отсчета есть поступательное движение, то 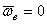и поэтому поворотное ускорение точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда 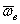в данный момент времени обращается в нуль.

Кроме того, поворотное ускорение точки может, очевидно, обращать­ся в нуль, если:

а) вектор относительной скорости 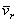точки параллелен вектору уг­ловой скорости 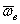переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;

б) точка не имеет движения относительно подвижной системы от­счета или относительная скорость 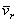точки в данный момент времени равна нулю ().

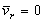Пример 14. Пусть тело вращается вокруг неподвижной оси z. По поверхности его движется точка М (рис. 52). Конечно, скорость этого движения точки – относительная скорость , а скорость вращения тела – угловая скорость переносного движения .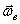

Ускорение Кориолиса , направлено перпен­дикулярно этим двум векторам, по правилу направления вектора век­торного произведения. Так, как пока­зано на рис. 52.

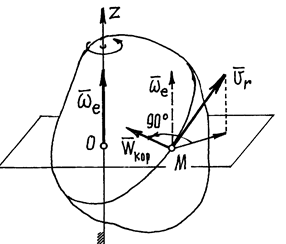
Рис.52

Нетрудно сформулировать более удобное правило определения направ­ления вектора 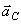: нужно спроектировать вектор относитель­ной ско­рости на плоскость перпендикуляр­ную оси переносного вращения и за­тем повер­нуть эту проекцию на 90 градусов в плоскости по направлению переносного вращения. Конечное положение проекции вектора укажет направление кориолисова ускорения. (Это правило было предложено Н.Е. Жуковским).

Пример 15. (Вернемся к примеру 13). Найдем абсолютное ускорение колечка М:

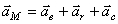. (6)

Переносное ускорение при движении колечка по окружности радиусом 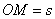: , где .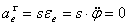

Значит (рис.53).

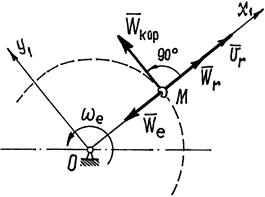
Рис.53

Относительное ускорение .

Ускорение Кориолиса .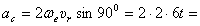

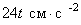Вектор 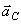направлен перпендикулярно стержню в сторону вращения (по правилу Жуковского).

Величину абсолютного ускорения колечка М найдем с помощью проекций на подвижные ос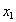и и 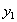проектируя равенство (6) на оси, получим: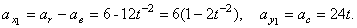

Тогда 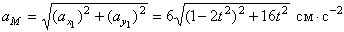.