
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения, допускающие понижение порядка.
|
|
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y(n) = f(x).
Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

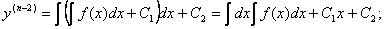
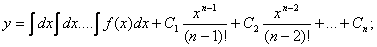
26-27) В математике линейное дифференциальное уравнение имеет вид
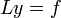
где дифференциальный оператор L линеен, y — неизвестная функция 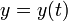 , а правая часть
, а правая часть 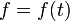 — функция от той же переменной, что и y.
— функция от той же переменной, что и y.
Линейный оператор L можно рассматривать в форме
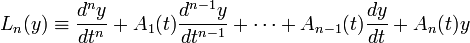
Вронскиа́ н (определитель Вронского) системы функций 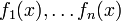 , дифференцируемых на промежутке I (n-1)-раз — функция на I, задаваемая определителем следующейматрицы:
, дифференцируемых на промежутке I (n-1)-раз — функция на I, задаваемая определителем следующейматрицы:
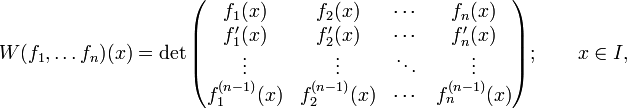 .
.
Также вронскианом называют функцию, заданную определителем более общего вида. А именно, пусть задано n вектор-функций 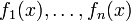 с n компонентами:
с n компонентами: 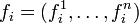 . Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его W 2):
. Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его W 2):
 .
.
Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.
Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.
Иными словами любые n линейно независимых решений y 1(x), y 2(x),..., yn (x) уравнения y (n) + an -1(x) y (n - 1) +... + a 1(x) y ' + a 0(x) y = 0 образуют фундаментальную систему решений.
28) Интегрирование ЛОДУ второго порядка с постоянными коэффициентами
Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.
Пусть дано ЛОДУ второго порядка
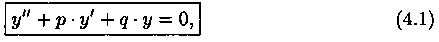
где р и q постоянны.
Для нахождения общего решения уравнения (4.1) достаточно найти два его частных решения, образующих фундаментальную систему (см. теорему 3.5).
Будем искать частные решения уравнения (4.1) в виде

где k - некоторое число (предложено Л. Эйлером). Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение (4.1), получим:
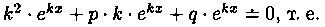
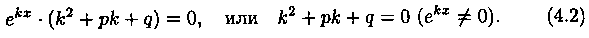
Уравнение (4.2) называется характеристическим уравнением ДУ (4.1) (для его составления достаточно в уравнении (4.1) заменить у", у' и у соответственно на k2, k и 1).
При решении характеристического уравнения (4.2) возможны следующие три случая.
Случай 1. Корни k1 и k2 уравнения (4.2) действительные и различные:
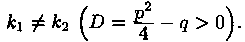
В этом случае частными решениями уравнения (4.1) являются функции y1=ek1x и у2=еk2x. Они образуют фундаментальную систему решений (линейно независимы), т. к. их вронскиан
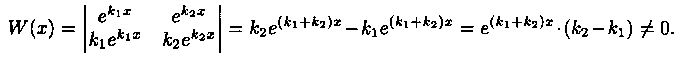
Следовательно, общее решение уравнения (4.1), согласно формуле (3.16), имеет вид

29)