
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Сначала построим математическую модель поставленной задачи и разработаем последовательность действий (алгоритм)
|
|
Сначала построим математическую модель поставленной задачи и разработаем последовательность действий (алгоритм). Итак, вычислим объем, занимаемый каждым контейнером: V = a·b·c. Далее, определим, какое максимальное количество контейнеров можно разместить по длине трюма (К1), по ширине (К2) и в высоту (К3). (Замечание: поскольку мы описываем линейный процесс, вопрос оптимизации размещения по длине и ширине не рассматривается!). Теперь подсчитаем общее количество погружаемых контейнеров и, наконец, общий вес груза.
Представим «словесный» алгоритм в виде блок-схемы. Чтобы можно было использовать этот алгоритм при любых размерностях контейнеров и трюма, введем обозначения: a – длина контейнера, b – ширина, c – высота, А – длина трюма, В – его ширина, С - высота, Р - вес одного контейнера.
Обратите внимание на то, что в блоках присваивания К1=целое(К1), К2=целое(К2), К3=целое(К3) влевой и правой части используется одно и то же имя переменной. Это означает, что сначала вычисляется оператор, стоящий в правой части, а полученное значение вносится в ячейку с именем левой части, т.е. изменяется содержимое ячейки.



|
 |

|
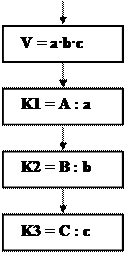 |
 |
Рис. 4. Блок-схема линейного процесса (задача 2)