
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Команда ветвления
|
|
В некоторых случаях, составляя алгоритм необходимо учитывать определенные условия, от которых зависят дальнейшие действия. Рассмотрим выражение 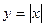 . Из математики мы знаем, если
. Из математики мы знаем, если 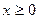 , то его модулем является то же самое число, если же
, то его модулем является то же самое число, если же 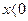 , то модулем является число ему противоположное.
, то модулем является число ему противоположное.
Чтобы составить алгоритм для такого выражения нужно знать команду ветвления.
Общий вид команды ветвления:
| если условие то серия 1 иначе серия 2 все |
На условие всегда дается однозначный ответ, только «да» или «нет». В случае ответа «да» на условие исполняются команды, записанные за словом то. В случае ответа «нет» на условие исполняются слова, записанные за словом иначе.
Допускается сокращенная форма команды ветвления, в которой отсутствует слово иначе.
| если условие то серия все |
Запишем алгоритм для вычисления модуля действительного числа:
алг модуль (вещ х, у)
арг х
рез у
нач
если 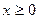 то у = х
иначе у = -х
все
кон
то у = х
иначе у = -х
все
кон
|
Запишем алгоритм решения квадратного уравнения:
алг квадратное уравнение (вещ 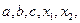 лит лит 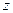 )
арг )
арг 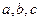 рез
рез 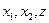 начвещ
начвещ 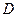
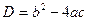 если
если 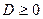 то
то 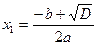
 иначе
иначе 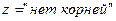 все
кон
все
кон
|
При построении алгоритма для решения квадратного уравнения, мы рассуждали так. Общий вид квадратного уравнения:
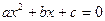 .
.
Для того, чтобы решить квадратное уравнение, необходимо вычислить дискриминант по формуле: 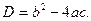 Затем сравнить дискриминант с нулем, если
Затем сравнить дискриминант с нулем, если 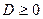 , то уравнение имеет два корня, которые вычисляются по формулам:
, то уравнение имеет два корня, которые вычисляются по формулам: 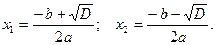 Если
Если  , то из него нельзя извлечь корень, а это значит, что корней уравнение иметь не будет.
, то из него нельзя извлечь корень, а это значит, что корней уравнение иметь не будет.
Блок-схема команды ветвления:
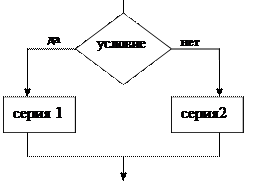
Служебному слову если соответствует ромб, у которого меньшая диагональ расположена вертикально, а большая – горизонтально. Внутри ромба пишется условие. Служебным словам то и иначе соответствуют два плеча, отходящих от ромба, на которых пишутся ответы «да» и «нет». Серии команд соответствует прямоугольник. Внутри прямоугольника пишутся команды. Служебному слову все соответствует стрелка-выход из блока.
Блок-схема решения квадратного уравнения:
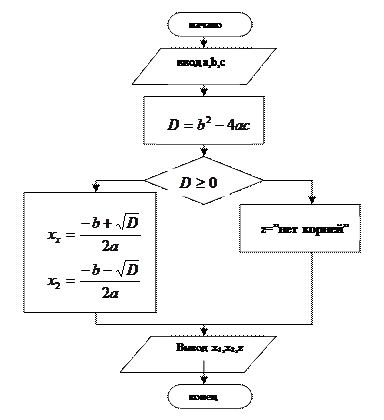
В алгоритме решения квадратного уравнения целью, которую мы должны были достичь, было – получить корни или убедиться в их отсутствии, т. е. решить квадратное уравнение. Поставим другую цель: определить количество корней квадратного уравнения. Изменилась цель – изменился и алгоритм. Построим алгоритм для достижения указанной цели. Нам не нужны переменные х1 и х2, так как корни мы не будем находить, для ответа на поставленный вопрос нам хватит литерной величины z.
алг квадратное уравнение 2 (вещ 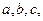 лит лит 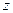 )
арг )
арг 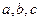 рез
рез 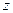 начвещ
начвещ 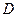
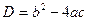 если
если 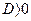 то
то 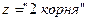 иначеесли
иначеесли 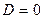 то
то 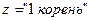 иначе
иначе 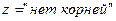 все
все
кон
все
все
кон
|
Построим блок-схему: 
В алгоритме внутри команды ветвления находится еще одна команда ветвления.
Построим алгоритм на слова из сказки: «Направо пойдешь – коня потеряешь, налево пойдешь – смерть найдешь, прямо пойдешь – друга найдешь».
| алг сказка нач если направо пойдешь то коня потеряешь иначеесли налево пойдешь то смерть найдешь иначе друга найдешь все все кон |