
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
II. Сущность и этапы корреляционно-регрессионного анализа (КРА).
|
|
I. Взаимосвязи экономических явлений и их виды.
Различные явления, происходящие в экономике, находятся в причинно-следственной связи. Эти связи многообразны по своему характеру и различны по свей силе.
Задача статистики сводится к тому, чтобы определить эти зависимости и дать им экономическую оценку. Для этого выделяют результативный (у) и факторные (х) признаки. Признак, характеризующий следствие называется результативным. Признаки, характеризующие причину – факторными.
Виды взаимосвязей:
1. По тесноте.
А) Функциональные (полная связь).
Возникает, когда значению величины факторного признака будет соответствовать определённое значение признака результата.
Пример: Зависимость уровня оплаты труда работников (результативный признак): от объёмов выполненной работы или от времени (факторные признаки).
Б) Корреляционная связь (частичная).
Возникает, когда отдельному значению факторного признака может соответствовать несколько значений признака результата.
Пример: Зависимость урожайности сельскохозяйственных культур (результативные признак) от дозы вносимых удобрений (факторный признак). Она может проявляться, а может не проявляться, т.к. урожайность зависит и от других факторов: сроков посева, погодных условий, уровня агротехники и других – которые либо усиливают эту связь, либо нивелируют её.
2. По направлению.
А) Прямая.
Проявляется, если направление изменения факторного и результативного признаков совпадают.
Пример: Рост прибыли (факторный признак) повышает уровень рентабельности (результативный признак) и наоборот.
Б) Обратная.
Проявляется, если направления признаков не совпадают.
Пример: Рост себестоимости (факторный признак) снизит уровень рентабельности (результативный признак) и наоборот.
3. По аналитической форме.
А) Линейная.
Проявляется, если зависимость результативного признака от факторного можно выразить уравнением прямой линии:
ух = а ± bх
б) Криволинейная.
Проявляется, если зависимость результативного признака от факторного выражается уравнением кривой:
ух = а ± b / х – гипербола;
ух = а ± bх ± сх2 – парабола второго порядка.
Уравнение, с помощью которого дается оценка зависимости называется уравнением регрессии.
4. По числу факторов.
А) Парная. Возникает когда рассматривается влияние одного факторного признака на результат.
Б) Множественная. Возникает, когда рассматривается влияние двух и более факторных признаков на результат.
II. Сущность и этапы корреляционно-регрессионного анализа (КРА).
Корреляционно-регрессионный анализ дает количественную оценку наличия и направления взаимосвязей, характеризует силу и форму влияния одних факторов на другие.
Задачи регрессионного анализа: выявить наличие зависимости, установить форму связи и дать оценку абсолютной зависимости результата от фактора. Они решаются с помощью обработки массового потока информации и определения коэффициентов: регрессии и эластичности.
Задача корреляционного анализа: измерить тесноту связи между признаками. Решается с помощью определения коэффициентов: корреляции и детерминации.
Этапы корреляционно-регрессионного анализа.
1. Постановка задачи и предварительное установление причинно-следственных связей.
2. Отбор наиболее существенных признаков и сбор фактического материала.
3. Выбор показателей для оценки взаимосвязей и установление формы связи.
а) С помощью группировки данных определяется, какие показатели брать для расчета характеристик взаимосвязи.
б) С помощью построения графика зависимости определяется форма связи.
4. Расчет числовых характеристик и их экономический анализ.
А) Однофакторный корреляционно-регрессионный анализ (на примере парной корреляции линейной регрессии).
Для выявления связи между признаками строится аналитическая таблица или корреляционная матрица:
| Х У | У1 | У2 | Уz | Итого |
| Х1 | f11 | f12 | f1z | Σ f1j |
| Х2 | f21 | f22 | f2z | Σ f2j |
| Хk | fk1 | fk2 | fkz | Σ fkj |
| Итого | Σ fi1 | Σ fi2 | Σ fiz | Σ fij = n |
fij – количество сочетаний значений х и у (частоты).
Если fij расположены в таблице беспорядочно, то связь между признаками отсутствует.
Если образуется какое-либо характерное сочетание fij – связь имеет место.
Пример: Если частоты в таблице концентрируются около одной из двух диагоналей – связь линейная.
Наглядным изображением корреляционной зависимости служит корреляционное поле (график), где на оси х откладываются значения факторного признака, оси у – результативного.
По расположению и концентрации точек судят о наличии и форме связи.
у у
 |  |
….................
…..........
….. …………………..
….. …………….
… ………………………
 …. х ……............. х
…. х ……............. х
а) линейная связь б) связь отсутствует
В случае парной линейной зависимости строится регрессионная модель:
ух = а ± bх, где (1)
± – характеризует направление связи ((–) – обратную, (+) – прямую);
ух – значение признака результата;
х – значение признака фактора;
а – свободный член уравнения;
b – коэффициент регрессии.
Коэффициент регрессии характеризует меру абсолютной зависимости результативного признака от факторного. Он имеет те же единицы измерения, что и признак результат и показывает, как изменяется признак результат при изменении факторного признака на единицу.
Параметры уравнения регрессии (а и b) находятся методом наименьших квадратов на основе решения системы уравнений (линейного):
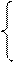 Σ у = аn + b х Σ х
Σ у = аn + b х Σ х
Σ ху = а х Σ х + b х Σ х2
Относительную характеристику регрессионной зависимости дает коэффициент эластичности:
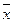
 Э = b х, где (2)
Э = b х, где (2)

х̅ ̅ – среднее значение факторного признака;
у̅ ̅ – среднее значение результативного признака.
Этот показатель характеризует среднее изменение результативного признака (в %) при изменении факторного на 1%.
Количественная оценка тесноты связи производится с помощью коэффициента парной корреляции (в нашем случае линейной):
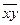 –
– 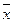 х
х 
 rух =, где (3)
rух =, где (3)
δ х х δ у
δ х – среднее квадратическое отклонение факторного признака;
δ у – среднее квадратическое отклонение результативного признака;
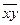 – среднее значение произведения факторного и результативного признака.
– среднее значение произведения факторного и результативного признака.
Коэффициент корреляции принимает значения от –1 до 1.
Если rух = 0 – линейная связь отсутствует;
если | rух | = 1 – связь полная (функциональная);
если | rух | < 0, 3 – связь слабая;
если | rух | – 0, 3 … 0, 7 – связь средняя;
если | rух | – 0, 7 … 0, 99 – связь сильная или тесная.
Для анализа относительной величины связи определяется коэффициент детерминации:
D = r2 х 100% (4)
Он показывает, сколько % вариации результативного признака обусловлено влиянием факторного.
Определение параметров корреляционно-регрессионной зависимости предполагает оценку надежности (значимости) коэффициента корреляции.
С этой целью определяют:
1) t-критерий (критерий Стьюдента):

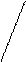 n – 2
n – 2


 tкр = r х, где (5)
tкр = r х, где (5)
1 – r2
(n – 2) – число степеней свободы при заданном уровне значимости α и объёме выборки n.
2) Фактическое значение t-кр сравнивается с табличным (для α = 0, 1; 0, 01 или 0, 05). Если фактическое значение t-кр превосходит табличное, то коэффициент корреляции значим (связь реальна).
Б) Множественный корреляционно-регрессионный анализ (на примере линейной регрессии).
При проведении этого анализа определяется перечень независимых переменных (факторных признаков), включаемых в уравнение регрессии.
Далее производится отбор наиболее значимых переменных и решается вопрос о форме уравнения (форме связи).
Уравнение линейной множественной регрессии:
ух = а ± b1х1 ± b2х2 ± … ± bnхn, где (6)
ух – значение признака результата, обусловленное влиянием нескольких признаков факторов;
х1, х2, …, хn – значения факторных признаков;
b1, b2, …, bn – коэффициенты регрессии, каждый из которых показывает на сколько единиц изменится результативный признак в связи с изменением соответствующего факторного признака на единицу при условии постоянства остальных значений х.
Для множественной регрессии определяются частные коэффициенты эластичности:
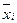
 Э = bi х, где (7)
Э = bi х, где (7)

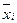 – среднее значение соответствующего факторного признака;
– среднее значение соответствующего факторного признака;
bi – коэффициент регрессии при соответствующем факторном признаке.
Этот коэффициент характеризует, на сколько процентов изменится результативный признак при изменении факторного на 1% при фиксированном значении остальных факторов.


 Для оценки тесноты связи между результативным и факторными признаками определяют коэффициент множественной корреляции (в нашем случае линейный):
Для оценки тесноты связи между результативным и факторными признаками определяют коэффициент множественной корреляции (в нашем случае линейный):
δ 2ост δ 2





 R = 1 – =, где (8)
R = 1 – =, где (8)
σ 2 σ 2
δ 2ост – остаточная дисперсия, характеризующая вариацию результативного признака за счет факторов, не включенных в уравнение множественной регрессии;
σ 2 – общая дисперсия фактических данных результативного признака;
δ 2 – дисперсия теоретических значений результативного признака, рассчитанная по уравнению множественной регрессии.
Этот коэффициент изменяется от – 1 до 1 и имеет туже интерпретацию, что и парный коэффициент регрессии. Чем он ближе к 1, тем связь более существенна.
Для анализа тесноты связи между факторным и результативным признаками при фиксированном значении других факторных признаков определяются частные коэффициенты корреляции.
Пример: Частный коэффициент корреляции между признаками х1 и у, при исключении влияния признака х2 определяется:
rух1 – rух2 rх1х2


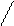 rух1(х2) =, где (9)
rух1(х2) =, где (9)

 (1 – r2ух2) (1 – r2х1х2)
(1 – r2ух2) (1 – r2х1х2)
r – парные коэффициенты корреляции между соответствующими признаками, определённые по формуле парного линейного коэффициента корреляции (формула 3).
Для характеристики тесноты связи между одним факторным и результативным признаком определяют парные коэффициенты корреляции (как при однофакторном). Они сводятся в корреляционную матрицу:

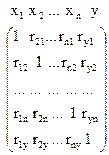
Если парный коэффициент корреляции между факторными признаками больше 0, 8, то взаимосвязь между ними мультиколлинеарна. Для получения адекватной модели регрессии необходимо устранить мультиколлениарность, т.е. исключить из неё факторные признаки, имеющие между собой тесную взаимосвязь.
Для определения факторов, в развитии которых заложены наиболее крупные резервы увеличения результативного признака определяют β -коэффициенты.
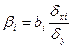 ,
,
Где 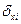 - среднее квадратическое отклонение i-го факторного признака;
- среднее квадратическое отклонение i-го факторного признака;
 - коэффициент регрессии i-го факторного признака.
- коэффициент регрессии i-го факторного признака.
β -коэффициент показывает какой фактор оказывает наибольшее влияние на результативный признак.
Для определения доли влияния анализируемого фактора от суммарного влияния всех факторов на результат определяют ∆ -коэффициенты:
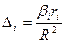 ,
,
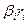 - показатель силы влияния соответствующего фактора на результат;
- показатель силы влияния соответствующего фактора на результат;
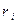 - парный коэффициент корреляции i-го факторного признака;
- парный коэффициент корреляции i-го факторного признака;
R2 – коэффициент множественной детерминации.
Множественный коэффициент детерминации:
D = R2 х 100% (10)
Он показывает, какая часть вариации результативного признака зависит от влияния включенных в модель факторных признаков.
Для определения степени влияния одного факторного признака на результативный определяют частные коэффициенты детерминации (формула 4).
Оценка значимости коэффициента множественной корреляции осуществляется на основе F-критерия (критерия Фишера).
Фактическое значение Fкр определяется по формуле:
R2 n – m

 Fкр = х, где (11)
Fкр = х, где (11)
1 – R2 m – 1
m – общее количество признаков (параметров уравнения);
n – объем выборки.
Фактическое значение Fкр сравнивается с табличным, которое находится с учетом заданного уровня значимости α (для α = 0, 01 или 0, 05) и числа степеней свободы k1 = m – 1 и k2 = n – m. Если фактическое значение больше фактического корреляция признаётся существенной.
III. Непараметрические методы оценки связей.
Методы оценки тесноты связи подразделяются на параметрические и непараметрические.
Параметрические методы основаны на использовании количественных характеристик признака: средних, дисперсии и других (корреляционный анализ).
Непараметрические методы позволяют измерять связь между качественными признаками.
Пример: а) зависимость между профессией и здоровьем;
б) зависимость успеваемости студентов заочников от работы их по специальности.
Непараметрические методы анализа.
1. При определении тесноты связи между двумя альтернативными признаками, представленными группами с противоположными характеристиками (хороший, плохой; успевающий, не успевающий и т.п.) определяются коэффициенты контингенции и ассоциации.
Для их расчёта используется таблица «четырех полей»:
| a | b | a + b |
| c | d | c + d |
| a + c | b + d | a + b + c + d |
a, b, c, d – частоты сочетаний пар качественных признаков.
1) Коэффициент ассоциации.
ad – bc
 Ка = (12)
Ка = (12)
ad + bc
2) Коэффициент контингенции.
ad – bc


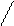 Кк = (13)
Кк = (13)

 (a + b) х (b + d) х (a + c) х (c + d)
(a + b) х (b + d) х (a + c) х (c + d)
Эти коэффициенты изменяются от – 1 до 1. Чем ближе их значение к 1, тем сильнее связаны между собой изучаемые признаки. Связь считается подтвержденной, если Ка ≥ 0, 5, а Кк ≥ 0, 3.
2. При определении тесноты связи между качественными признаками, состоящими из более двух групп определяются коэффициенты К. Пирсона и А.А. Чупрова.
С этой целью строится таблица сопряжённости.
| Группы признака – Х | Группы признака – У | Итого | ||
| I | II | III | ||
| I | f1ух | f2ух | f3ух | nх1 |
| II | f4ух | f5ух | f6ух | nх2 |
| III | f7ух | f8ух | f9ух | nх3 |
| Итого | nу1 | nу2 | nу3 | nух |
fух – частоты сочетания признаков х и у;
nх – сумма частот строки;
nу – сумма частот столбца;
nух – сумма частот сочетаний х и у.

 1) Коэффициент взаимной сопряженности К. Пирсона.
1) Коэффициент взаимной сопряженности К. Пирсона.
φ 2


 Кп =, где (14)
Кп =, где (14)
1 + φ 2
φ 2 = Σ zi – 1, где
zi – значение расчётного показателя, определённого по i-й строке.
 (f1ух)2 (f2ух)2 (f3ух)2
(f1ух)2 (f2ух)2 (f3ух)2


 z1 = + +: nх1;
z1 = + +: nх1;
nу1 nу2 nу3
 (f4ух)2 (f5ух)2 (f6ух)2
(f4ух)2 (f5ух)2 (f6ух)2


 z2 = + +: nх2;
z2 = + +: nх2;
nу1 nу2 nу3
 (f7ух)2 (f8ух)2 (f9ух)2
(f7ух)2 (f8ух)2 (f9ух)2


 z3 = + +: nх3.
z3 = + +: nх3.
nу1 nу2 nу3
2) Коэффициент взаимной сопряженности Чупрова.
φ 2


 Кп =, где (15)
Кп =, где (15)
(k1 – 1) (k2 – 1)
k1 – число групп по строкам;
k2 – число групп по колонкам.
Эти коэффициенты изменяются от 0 до 1. Чем они ближе к 1, тем связь теснее.