
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Материалов с жидкой фазой
|
|
В традиционных процессах горячей обработки давлением инертных порошков объектом теоретических и экспериментальных исследований обычно служат материалы, содержащие два основных элемента структуры - поры и твердую фазу. Для описания процесса пластического деформирования и уплотнения таких материалов достаточно информации о реологических свойствах твердой фазы и виде функций пористости. Результаты анализа теплового режима, выполненного в разд. 2, показали, что в широком диапазоне изменения технологических параметров температура продуктов синтеза системы Ti-C-Ni выше эвтектической, и они находятся в твердожидком состоянии. В работах [17, 215, 234] также отмечается, что горячие продукты СВС содержат, кроме пор и твердой фазы, третий элемент структуры – жидкую фазу, образованную расплавом легкоплавких компонентов. Для описания реологического поведения твердожидких СВС-материалов используются представления механики континуума [17, 82], однако в указанных работах определяющие уравнения содержат только реологические константы твердой фазы и функции пористости, но не учитывают присутствие расплава. Следуя работе [203], рассмотрим влияние жидкой фазы на реологические свойства вязких пористых тел.
Однородное изотермическое течение сжимаемого линейно-вязкого тела полностью описывается уравнением неразрывности
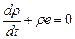 (3.1)
(3.1)
и определяющими соотношениями
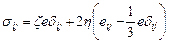 , (3.2)
, (3.2)
где z, h – коэффициенты объемной и сдвиговой вязкости. Для двухэлементной структуры (поры и твердая фаза) коэффициенты объемной z и сдвиговой h вязкости связаны с функциями пористости y и j зависимостями [186, 230]
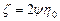 ;
;  , (3.3)
, (3.3)
где h 0 – сдвиговая вязкость твердой фазы. При функциях пористости, принятых в виде [186, 230]
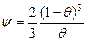 ,
, 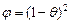 , (3.4)
, (3.4)
коэффициенты вязкости равны
 ,
, 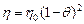 . (3.5)
. (3.5)
Здесь q – объемная доля пор или пористость.
На основе метода самосогласования и методологии работы [184] найдем соответствующие зависимости для коэффициентов вязкости z и h в случае пористого твердожидкого тела. Согласно принципу упруго-вязкой аналогии сначала рассмотрим упругое тело, а затем выполним обобщение на линейно-вязкое тело.
Выделим элементарную ячейку в виде сферической поры радиусом R 1, которая вместе с жидкой оболочкой радиусом R 2 помещена в сжимаемую среду с модулем объемного сжатия K и модулем сдвига m (рис. 3.1). Количественное содержание трех элементов среды определяется объемными концентрациями твердой rS и жидкой m фаз, а также пористостью q:
 . (3.6)
. (3.6)
 Сумма объемных концентраций твердой и жидкой фаз представляет собой относительную плотность пористой среды:
Сумма объемных концентраций твердой и жидкой фаз представляет собой относительную плотность пористой среды:
 . (3.7)
. (3.7)
Количество жидкой фазы определяется в соответствии с диаграммой фазового равновесия для беспористого материала при q = 0. Параметр m, который определен для пористого состояния, связан с объемной концентрацией расплава mL в беспористой конденсированной фазе зависимостью
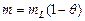 . (3.8)
. (3.8)
С учетом (3.8) для относительной плотности твердожидкого тела имеем
 . (3.9)
. (3.9)
Рассмотрим равновесие ячейки, когда к ее внешней границе приложено давление р; давление внутри поры отсутствует. Так как на поверхности поры радиальное напряжение sr (R 1) = 0, то в случае идеальной жидкости в области R 1< r < R 2 давление равно нулю. В силу непрерывности нормального напряжения радиальное напряжение на границе жидкой фазы также равно нулю: sr (R 2) = 0 [199]. В результате имеем задачу о равновесии упругой сферической ячейки с граничными условиями sr (R 2) = 0 и sr (R 3) = - p.
Для произвольной пористости в [184] рассматривается неограниченная среда с R 3 = ¥. В этом случае из решения Лифшица-Ландау [94] радиальное смещение на границе жидкой фазы u 2 при r = R 2 будет равно
 . (3.10)
. (3.10)
Принимая во внимание условие несжимаемости расплава
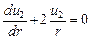 , (3.11)
, (3.11)
найдем радиальное смещение на границе поры при r = R 1
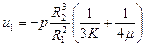 (3.12)
(3.12)
и среднюю объемную микродеформацию поры
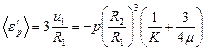 . (3.13)
. (3.13)
Осредненный по объему ячейки тензор упругой деформации e ij пористого тела определяется из зависимости
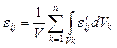 , (3.14)
, (3.14)
где V – объем ячейки; Vk – объем k -того структурного элемента ячейки;  – тензор упругих микродеформаций. Из теоремы Остроградского-Гаусса найдем тензор упругой деформации [36, 199]
– тензор упругих микродеформаций. Из теоремы Остроградского-Гаусса найдем тензор упругой деформации [36, 199]
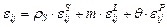 (3.15)
(3.15)
и объемную деформацию пористого тела
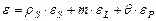 . (3.16)
. (3.16)
Здесь и далее индексы S, L и P относятся соответственно к твердой, жидкой и газообразной фазам. Так как твердая и жидкая фазы несжимаемы (eS = eL = 0), то получим
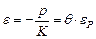 . (3.17)
. (3.17)
Принимая условие эргодичности, объемную деформацию поры eР найдем путем осреднения объемной микродеформации 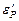 по объему, занимаемому всеми порами:
по объему, занимаемому всеми порами:
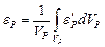 . (3.18)
. (3.18)
Используя в качестве 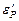 среднюю микродеформацию
среднюю микродеформацию 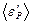 , определяемую выражением (3.13), получим
, определяемую выражением (3.13), получим
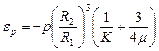 , (3.19)
, (3.19)
что после подстановки в (3.17) дает
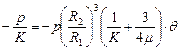 . (3.20)
. (3.20)
Из геометрии элементарной ячейки (см. рис. 3.1) следует, что
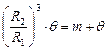 . (3.21)
. (3.21)
Подставив (3.21) в (3.20), найдем зависимость между модулем объемного сжатия K и модулем сдвига m для упругого пористого твердожидкого тела:
 . (3.22)
. (3.22)
Следуя принципу упруговязкой аналогии, перейдем к зависимости между коэффициентами объемной z и сдвиговой h вязкости:
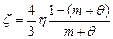 . (3.23)
. (3.23)
Зависимости (3.22) и (3.23) получены при условии, что жидкая фаза находится в незамкнутом объеме при q ¹ 0 и давление на ее поверхности отсутствует. В этом случае жидкая и газообразная фазы оказывают аддитивное влияние на сжимаемость пористой среды. В замкнутом объеме жидкость проявляет свое свойство несжимаемости, и при q = 0 объемная вязкость твердожидкого тела скачкообразно возрастает до бесконечности. Разрывный характер зависимости z (q) можно учесть индикаторной d -функцией, определенной следующим образом:
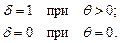 (3.24)
(3.24)
Тогда зависимость (3.23) примет вид
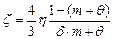 . (3.25)
. (3.25)
Рассмотрим точное решение для эффективного модуля сдвига m упругой среды с несжимаемой матрицей и малой объемной концентрацией сферических включений с 1 [89, 184]:
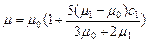 , (3.26)
, (3.26)
где m 0, m 1 – модули сдвига матрицы и включения соответственно. Сопротивление сдвигу в расплаве на несколько порядков ниже, чем сдвигу в твердом состоянии, и в приближении идеальной жидкости им можно пренебречь. Тогда жидкую и газообразную фазы можно рассматривать как одно включение с m 1 = mL = mP = 0 и выполнить простое суммирование объемных концентраций этих фаз [165]:
с 1 = m + q. В результате для упругого пористого твердожидкого тела получим
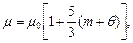 (3.27)
(3.27)
а для вязкой среды
 (3.28)
(3.28)
Обобщение зависимости (3.28) на случай произвольной пористости, выполненное по методике работы [184], приводит к выражению
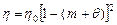 . (3.29)
. (3.29)
Из сопоставления соотношений (3.5), (3.25) и (3.29) следует, что влияние жидкой фазы на реологические свойства вязкой сжимаемой среды формально проявляется в суммировании объемной доли расплава m и пористости q. При отсутствии жидкой фазы (m = 0) зависимости (3.25), (3.29) для пористого твердожидкого тела переходят в соответствующие зависимости (3.5) для пористого твердого тела. При одинаковой пористости q наличие жидкой фазы приводит к уменьшению объемной z и сдвиговой h вязкости и к увеличению скорости уплотнения пористого твердожидкого тела по сравнению с пористым твердым телом. Более низкое сопротивление сдвигу в твердожидком теле характерно и для беспористого состояния.
В пористом твердожидком теле мерой плотности служит объемная доля конденсированной фазы r, которая равна сумме объемных концентраций жидкой m и твердой rS фаз. Параметр m, согласно зависимости (3.6), характеризует содержание жидкой фазы в пористом теле. Чтобы найти величину m, необходимо сначала по диаграмме состояния сплава определить количество жидкой фазы mL, поэтому целесообразно вместо параметра m использовать непосредственно объемную концентрацию расплава mL. Эта замена выполняется соотношением (3.9). Подставив (3.9) в (3.1), получим уравнение неразрывности, в которое входит только объемная концентрация твердой фазы rS:
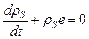 . (3.30)
. (3.30)
Выражения (3.25) и (3.29) для объемной и сдвиговой вязкости в функции rS запишутся как
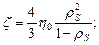
 , (3.31)
, (3.31)
а функции пористости или, точнее, плотности будут равны
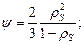
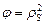 . (3.32)
. (3.32)
В формуле (3.31) для z опущена d -функция, отражающая скачкообразный переход твердожидкого тела в несжимаемое состояние. Этот эффект учитывается при решении уравнения (3.30) назначением верхнего предела интегрирования:  . Нижний предел интегрирования согласно (3.9) будет равен
. Нижний предел интегрирования согласно (3.9) будет равен  , где r 0 – начальная относительная плотность конденсированной фазы.
, где r 0 – начальная относительная плотность конденсированной фазы.
Таким образом, итоговые соотношения показывают, что в рамках модели со свободной поверхностью жидкой фазы реологические свойства вязкого пористого тела и кинетика его уплотнения определяются количеством и сдвиговой вязкостью вещества твердой фазы. Жидкая фаза в этой модели может рассматриваться как элемент поровой структуры, и информации об ее объемной концентрации достаточно для описания свойств уплотняемой среды. Эта реологическая модель пористого вязкого тела с жидкой фазой впервые была аксиоматически сформулирована в работе [239].
Корректность предлагаемой реологической модели пористого твердожидкого тела рассмотрим на примере решения обратной задачи реологии.
Вещества кристаллической природы в общем случае не являются ньютоновскими жидкостями, и их течение при повышенных температурах осуществляется по механизму нелинейной ползучести. Следуя работе [82], для описания процесса установившейся ползучести будем использовать степенной закон течения:
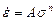 , (3.33)
, (3.33)
где 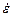 – скорость ползучести; А, n – эмпирические константы.
– скорость ползучести; А, n – эмпирические константы.
Показатель нелинейности течения n определяется при обработке результатов экспериментальных исследований. В работе [84] для этого используется обобщенное уравнение объемного вязкого течения пористого тела при одностороннем прессовании в жесткой пресс-форме с внешним трением:
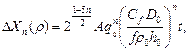 (3.34)
(3.34)
где А – коэффициент, зависящий от температуры; q 0 – давление на пуансоне; D 0 – диаметр пресс-формы; h 0 – начальная высота прессовки; f – коэффициент внешнего трения; t – время. Параметр Сf в уравнении (3.33) равен
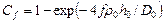 . (3.35)
. (3.35)
В уравнении (3.34) разность первообразных функций D Xn (r), взятых для текущего r и начального r 0 значений относительной плотности, определяется следующим выражением [82, 84]:
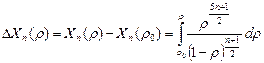 . (3.36)
. (3.36)
Неизвестный параметр n определяют путем варьирования его величины до тех пор, пока зависимость ² D Xn (r) - t ² не станет линейной.
В работе [84] исследовалась кинетика уплотнения порошка твердого сплава ВК6 при температурах 1250 и 1300 оС, когда кобальтовая связка находится в расплавленном состоянии. Авторы исследования [84] рассматривали относительную плотность rконденсированной фазы в целом и пришли к выводу, что в присутствии жидкой фазы имеет место линейный характер течения и n = 1. В итоге процесс деформации трактуется как течение концентрированной суспензии твердых частиц карбида вольфрама WC в расплавленной кобальтовой фазе. Достижение беспористого состояния при таком механизме уплотнения возможно при условии, что объем жидкой фазы не меньше объема пор при плотнейшей упаковке частиц порошка. Так, для монодисперсных порошков в приближении сферических частиц относительная объемная доля жидкой фазы должна быть не менее 26% [3]. Для сплава ВК6 объемная доля кобальтовой связки составляет 10%, поэтому маловероятно, что уплотнение этого материала протекает без вязкой деформации карбидной фазы.
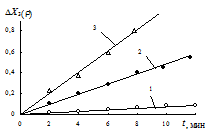
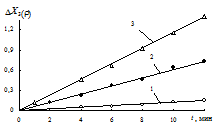
Были обработаны экспериментальные данные работы [84] с использованием табулированных значений функций Xn (r) из работы [21]. При этом вместо относительной плотности r рассматривалась объемная доля твердой фазы rS при объемной доле кобальтового расплава mL = 0, 1. Результаты расчетов показали, что зависимость ² D Xп (rS) - t ² является линейной при n = 3 (рис. 3.2). Точно такое же значение показателя нелинейности n получено в работе [21] при исследовании горячего прессования порошка карбида вольфрама WC. Следовательно, вязкая деформация твердожидкого сплава ВК6 при малом объеме жидкой фазы происходит за счет ползучести карбида вольфрама. Этот вывод является физически более обоснованным и свидетельствует о корректности предлагаемой реологической модели уплотнения пористого тела с жидкой фазой.
  а б
а б
|
| Р и с. 3.2. Зависимость параметра D X 3(rS) при спекании сплава ВК6 для 1250 оС (а) и 1300 оС (б) от времени t и давления q: 1 – q = 4, 9 МПа; 2 – q = 9, 8 МПа; 3 – q = 14, 7 МПа |