Процесса деформирования

Для решения краевых задач неустановившегося пластического деформирования несжимаемых и сжимаемых тел используется метод ² по шагам², согласно которому время деформирования разбивается на ряд временных интервалов. В пределах каждого шага решается краевая задача, которая состоит в определении распределения скоростей и напряжений. Точность решения метода ² по шагам² определяется величиной временного шага D t. При численных методах решения задач пластического деформирования с пространственной дискретизацией объекта результат решения зависит также и от размеров пространственных элементов.

При решении задачи нестационарного теплообмена горячих продуктов синтеза с оболочкой уже были получены оценки пространственно-временных координат конечно-элементной модели объекта. Механические процессы отличаются от теплофизических системой разрешающих уравнений, способами и алгоритмами решения задачи. Соответственно геометрические и временные параметры дискретных моделей процессов пластического деформирования и теплообмена будут различными. Искомые параметры конечно-элементной модели процесса пластического деформирования при СВС-прессовании определяются при исследовании на сходимость численного решения краевой задачи. Основные результаты исследования на сходимость изложены в работе [213].

На рис. 4.6 приведена схема дискретизации деформируемого объема на конечные элементы. В силу осевой симметрии рассматривается половина меридионального сечения в цилиндрических координатах. При разбиении на КЭ вся область сначала покрывается прямоугольной сеткой, а затем полученные прямоугольники диагоналями делятся на два треугольника. Исходными топологическими характеристиками дискретной модели служат число горизонтальных слоев заготовки Ns 1, число горизонтальных слоев нижней Ns 2 n и верхней Ns 2 v оболочек, число радиальных узлов заготовки Nr 1 и число радиальных узлов оболочки Nr 2. Геометрическими характеристиками являются радиусы заготовки R ₁ и матрицы R ₂, высота заготовки h ₁, толщина нижней h _2н и верхней h _2в оболочек. Размеры прямоугольной сетки характеризуют длина h_r по координате r и высота h_z по координате z (см. рис. 4.6). Глобальная нумерация узлов и конечных элементов, а также вычисление координат узлов, выполняются автоматически.

Алгоритм решения краевой задачи пластического деформирования со смешанными граничными условиями содержит две вычислительные процедуры, выполнение которых связано с получением заданной точности решения. Это итерационные циклы решения нелинейной задачи пластического течения методом переменной вязкости и расчета сил внешнего трения оболочки. Величина секущего модуля сдвиговой вязкости m_S и напряжений трения определяется плотностью продуктов синтеза и оболочки. В свою очередь плотность продуктов синтеза и оболочки зависит от времени и фактического параметра, управляющего точностью и сходимостью итерационных циклов – временного шага D t. Поэтому сначала было проведено исследование по выбору величины временного шага D t, обеспечивающего вычислительную эффективность итерационных циклов решения нелинейной задачи пластического деформирования и расчета сил трения.

Величина D t взаимосвязана с точностью выполняемого численного расчета e. Было проведено исследование на сходимость решения задачи изотермического пластического деформирования с варьированием точности расчета напряжений и сил трения. В качестве решения рассматривалось изменение средней плотности r ₁ заготовки из сплава TiC-20% Ni в зависимости от давления прессования q. Скорость перемещения пуансона составляла v ₀ = 8 мм/с. Температура заготовки принималась равной Т ₁ = 2270 ^оС, которая была получена путем осреднения решения тепловой задачи. Объемная доля расплава при этой температуре составляет m_L = 0, 27. Принималось, что песчаная оболочка имеет комнатную температуру. Использовалась равномерная сетка конечных элементов со следующими топологическими параметрами: Ns 1 = 6; Ns 2 n = Ns 2 v = 3; Nr 1 = 10; Nr 2 = 18. Геометрические размеры объектов были следующими: R ₁ = 39 мм;
R ₂ = 62, 5 мм; h ₁ = 14 мм; h _2н = h _2в = 10 мм.

При исследовании на сходимость нелинейной задачи пластического деформирования трение оболочки не учитывалось. За ошибку решения принималась величина относительной разности значений эквивалентных напряжений s(w) на двух последовательных итерациях. Рассматривалось два значения точности решения e _пл: e _пл = 5%, которое наиболее часто принимается в практике инженерных расчетов, и e _пл = 2%. Расчеты показали, что в этом случае погрешность расчета плотности не превышает 0, 2-0, 5%. Результаты расчетов, представленные на рис. 4.7, показывают, что уменьшение погрешности вычислений с e _пл = 5% до e _пл = 2% практически не оказывает влияния на результаты решения. Вместе с тем с увеличением точности решения резко увеличивается время расчета. Так, при решении с точностью e _пл = 5% время расчета составило 40 мин, а при решении с точностью e _пл = 2% – 2 ч 34 мин, т.е. почти в 4 раза больше (на ПЭВМ Pentium – IV с частотой процессора 1, 6 ГГц).

Установлено, что для стационарного макроструктурного состояния продуктов СВС (аэродисперсное или пространственно устойчивое) процесс сходится за 1-2 итерации при временном шаге D t = 0, 05 с. На стадии перехода от аэродисперсной к пространственно устойчивой структуре сходимость резко ухудшается. Так, при погрешности e _пл £ 5% с шагом D t = 0, 05 с процесс не сходится. Для обеспечения сходимости применялся алгоритм автоматического выбора шага по времени: если за 4 итерации процесс не сходится, то текущее значение D t уменьшается вдвое. После завершения итерационного процесса на текущем этапе нагружения для следующего этапа нагружения величина начального шага D t восстанавливается.

Р и с. 4.7. Влияние точности решения e пл на результат расчета средней плотности заготовки r 1: · – решение с e пл =5%; о – решение с e пл = 2%

Таким образом, при решении физически нелинейной задачи пластического течения методом переменной вязкости можно ограничиться точностью решения e _пл = 5%. Начальный шаг по времени при штатной скорости движения пуансона v ₀ = 8 мм/с не должен превышать значения D t ₀ = 0, 05 с.

При определении точности расчета сил трения e_тр решалась задача пластического деформирования с учетом внешнего трения оболочки. За ошибку решения принималась величина относительной разности значений узловых сил трения на двух последовательных итерациях. Точность решения нелинейной задачи пластического деформирования составляла e _пл = 5%; начальный шаг по времени
D t ₀ = 0, 05 с. Рассматривались два значения точности расчета сил трения e _тр: e _тр = 2% и e _тр = 5%. Согласно результатам расчетов (рис. 4.8) рассматриваемые значения точности не оказывают заметного влияния на результат решения задачи. При точности e _тр = 5% и шаге D t =0, 05 с процесс сходится уже на 1-й итерации. Исключение составляет первый шаг нагружения, на котором сначала решается задача без трения, а затем путем последовательных приближений вычисляются силы трения. На первом шаге нагружения расчет сил трения происходит за 3-4 итерации. Следует отметить, что увеличение точности расчета сил трения не оказывает такого сильного влияния на затраты машинного времени, как увеличение точности решения задачи пластического деформирования. Так, при увеличении точности решения с e _тр = 5% до e _тр = 2% время расчета практически остается неизменным: соответственно 1 ч 7 мин и 1 ч 15 мин (на ПЭВМ Pentium – IV с частотой процессора 1, 6 ГГц).

После выбора количественных характеристик временной координаты D t и точности решений в итерационных циклах определяются размеры пространственной сетки. Для этого было проведено исследование на сходимость численного решения краевой задачи пластического деформирования при СВС-прессовании. Для задач, имеющих точное аналитическое решение, сходимость оценивается сопоставлением численного и точного решений. При исследовании сходимости задач, для которых нет точного решения, применяют апостериорную оценку по правилу Рунге [90]. Сначала находят решение при шаге пространственных координат h, потом вычисляют решение при шаге h /2 и сравнивают значения y_h (x_i) и y_{h /2}(x_i) в одинаковых узлах:

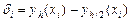, (4.46)

где d_i – ошибка решения в i -том узле; x_i – вектор узловых координат.

Затем выполняется проверка точности полученного решения:

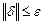. (4.47)

Здесь 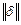– принятая норма ошибки решения; e – заданная точность решения задачи. Если условие (4.47) выполняется, то решение y_h (x_i) принимается за искомое. В противном случае шаг h /2 делят пополам и вычисляют решение y_{h /4}(x_i). Контроль точности в вычислении значений y_{h /4}(x_i) осуществляют аналогично предыдущему. Точного решения краевой задачи пластического деформирования при СВС-прессовании нет, и исследование численного решения на сходимость при определении размеров пространственной сетки необходимо выполнять по правилу Рунге.

В механике порошковых материалов и пористых тел главное внимание уделяется не исследованию напряженно-деформирован- ного состояния, а изучению параметров, характеризующих состояние материала и, в первую очередь, его плотности. При выборе временной координаты конечно-элементной модели и точности решений было установлено, что при СВС-прессовании в заготовке и оболочке формируется неоднородное поле плотности, поэтому в качестве решения краевой задачи рассматривалось распределение относительной плотности оболочки r ₂ по радиусу r ₂(r) при z = const и по высоте r ₂(z) при r = const деформируемого объема. Зависимость r ₂(r) определялась в горизонтальном слое, расположенном вдоль верхней опорной плоскости заготовки; зависимость r ₂(z) – в вертикальном столбце, прилегающем к боковой поверхности заготовки. За норму 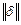принималась величина максимальной ошибки решения для зависимостей r ₂(r) и r ₂(z) по ансамблю конечных элементов:

. (4.48)

Здесь, как и при оценке временного шага D t и точности решений e _пл и e _тр, рассматривался процесс СВС - прессования круглых заготовок из сплава TiC-20% Ni радиусом R ₁ = 39 мм в пресс-форме с матрицей радиусом R _м = 62, 5 мм и при максимальном давлении прессования q =120 МПа. Начальная высота заготовки составляла h ₁₀=14 мм; толщина верхней и нижней оболочек – 10 мм. Начальный размер ячеек равномерной сетки принимался равным: для заготовки– h_r =4, 87 мм, h_z =3, 5 мм; для оболочки – h_r =4, 7 мм, h_z =5 мм. Геометрические и топологические характеристики дискретных моделей при измельчении размеров сетки приведены в табл. 4.2. Точность решения по величине плотности r ₂(r) и r ₂(z) составляла e =0, 2 %.

Зависимости r ₂(r) и r ₂(z) при варьировании размеров сетки конечных элементов представлены на рис. 4.9 и 4.10.

Существенное различие реологических свойств продуктов синтеза и песчаной оболочки обуславливает неоднородное распределение плотности в радиальном и осевом направлениях. По характеру изменения плотности следует выделить две области – с высокими и малыми градиентами плотности. На границе с ребрами заготовки, которые имеют нулевой радиус кривизны и являются концентраторами напряжений, происходит резкое увеличение плотности оболочки. В объемах, имеющих с заготовкой плоскую границу с бесконечным радиусом кривизны (r < 35 мм), распределение плотности близко к однородному и характеризуется малыми градиентами. В области с плоской границей и с малыми градиентами сходимость достигается на более крупных ячейках по сравнению с областью высоких градиентов плотности (рис. 4.9), поэтому после получения сходимости в области малых градиентов на следующем шаге измельчение сетки выполняли только в области высоких градиентов плотности.

Т а б л и ц а 4.2