
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое обоснование
|
|
Дисперсия проявлений признаков в популяциях
Теоретическое обоснование
Условием результативности отбора является генотипическая обусловленность хотя бы части наблюдаемой фенотипической изменчивости признака, подлежащего отбору. Мы с вами останавливались на этих аспектах успешности отбора. Чем больше доля генотипически обусловленной изменчивости признака в его общей фенотипической изменчивости, тем сильнее связь между генотипом и фенотипом и, следовательно, тем эффективнее отбор. Абсолютная связь между генотипом и фенотипом возможна только в гипотетическом случае, когда вся видимая фенотипическая изменчивость признака обусловлена генотипически. В этом случае достигается предельно высокая эффективность отбора (стопроцентная эффективность).
Добавить из Айала и др., 1988 Т.2 о соотношении генотипической и фенотипической долей с общей фенотипической дисперсии.
Мерой доли генотипически обусловленной изменчивости в общем фенотипическом варьировании служит коэффициент наследуемости.
Косвенно по коэффициенту наследуемости можно судить и о доле изменчивости, обусловленной влиянием среды: по разности между общей фенотипической изменчивостью и её долей, обусловленной генотипически.
П.Ф. Рокицкий (1978, стр. 201-202) считает, что предпосылкой для введения этого понятия в употребление при научном анализе строения популяций явился ряд обстоятельств. Оказалось, что применяемые на первоначальных этапах аналитической работы такие важнейшие биометрические показатели как «средняя величина признака в популяции» и «дисперсия проявлений признака в популяции», оцениваемая по среднему квадратическому отклонению, оказались недостаточными в работе с популяциями сложной структуры. В таких популяциях осуществляется большое число разнообразных скрещиваний, вследствие чего нет возможности оперировать анализом отдельных генов и пользоваться такими понятиями как «частота генов». И хотя с помощью оценок средних значений и дисперсии признаков удалось сделать существенные выводы об общей картине наследования количественных признаков и их генетической обусловленности отдельными генами, дальнейший анализ популяций требовал развития аналитических методов. Поэтому понадобились новые параметры для характеристики генетической структуры популяции по количественным признакам.
Подойти к пониманию принципа формирования новых методов анализа генетической структуры популяций можно следующим образом.
Любая варианта (значение признака) у какой-либо особи в популяции (например: значение диаметра ствола на высоте груди у конкретного дерева сосны и др.) имеет определенное фенотипическое значение «y» (например: диаметр равен y=36 см). Это фенотипическое значение может быть выражено как отклонение от популяционной средней «М» и может быть обозначено символом «Р». Тогда:
у – М = Р (например: 36см – 24см = +12см, следовательно Р = 12 см).
Так как вариация значений признака в популяции определяется в конечном счете двумя основными факторами: различиями в генетической структуре отдельных особей и влиянием средовых факторов, – то и для каждой отдельной особи её фенотипическое значение Р можно рассматривать как результат суммирования генотипического (G) и средового (E) отклонений.
P = G + E
Но из этого, конечно, не следует, что в фенотипе каждой особи можно выделить самостоятельные доли, зависящие от генотипа яйца, из которого развился данный фенотип, и от условий среды, в которых он развился. Фенотип особи – это единое целостное понятие. О генотипе особи непосредственно, без анализа её потомства, судить невозможно. Выделение же долей вариации, зависящих от наследственности и от среды, производится только для популяций.
Чтобы определить вариансы (оценки дисперсии через среднее квадратическое отклонение) отклонений G и E для популяции, надо возвести каждое отклонение в квадрат, затем просуммировать все отклонения и полученные суммы разделить на число объектов в популяции (если учет был сплошным) или в выборке из популяции (при выборочных методах анализа). При этом необходимо учитывать установленное выше равенство P = G + E.
Варианса – это мера дисперсии (изменчивости) признака у изучаемого объекта.
Дисперсия – это рассеивание значений признака, разброс значений признака.
Если мы возводим в квадрат левую половину равенства (именно для популяции), то должны возвести в квадрат и его правую половину для сохранения условия равенства, тогда получим:
P2 = (G + E)2 или P2 = G2 + E2 + 2GE
Далее, разделив каждый член равенства на численность объектов (в выборке или популяции) “n”, получим:
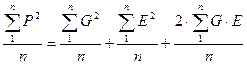
Но тогда мы сможем каждый из членов полученного равенства выразить в виде соответствующих дисперсий, а точнее, средних квадратов отклонений от среднего каждого конкретного значения признака, поскольку:
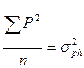 - общая фенотипическая дисперсия;
- общая фенотипическая дисперсия;
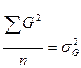 - генотипическая дисперсия;
- генотипическая дисперсия;
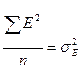 - дисперсия, вызванная влиянием среды.
- дисперсия, вызванная влиянием среды.
Сложнее стоит вопрос о величине 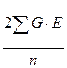 .
.
Ответить на него можно, исходя из следующих соображений. Поскольку величины G и E представляют собой генотипические и средовые отклонения, то сумма их произведений является ковариансой между этими отклонениями.

Как известно, коварианса входит в структуру коэффициента корреляции, а именно:
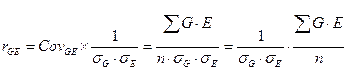
Тогда исходное уравнение можно представить в следующем виде:
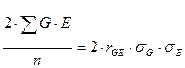
В таком случае первоначальное равенство примет вид:
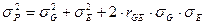
Изменения условий среды в пределах нормы реакции (и не связанные с эволюционными изменениями в чередующемся ряду поколений – этот аспект не рассматривается) не вызывают изменения генотипов особей вида, обитающих в границах территории, флуктуации экологических условий которой рассматриваются. Раметы одного клона, размещенные в разных местах на одной ЛСП, не изменят свой генотип в том или ином участке, как и в случае их размещения на других ЛСП. Тогда различия в генотипах разных клонов (клонов разных ПД) останутся стабильными и независимыми от условий среды.
Если предположить, что корреляция между вариацией генотипических и средовых факторов отсутствует или равна нулю, что вполне логично и вытекает из представлений о независимости в пределах нормы реакции варьирования, обусловленного генотипически, то формула примет знакомый нам вид:
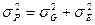 , где
, где
 - общая фенотипическая варианса;
- общая фенотипическая варианса;
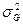 - доля общей фенотипической вариансы, зависящая от различий между отдельными особями популяции по их наследственности;
- доля общей фенотипической вариансы, зависящая от различий между отдельными особями популяции по их наследственности;
 - доля общей фенотипической вариансы, вызванная различиями в условиях внешней среды, при которых развивались особи популяции.
- доля общей фенотипической вариансы, вызванная различиями в условиях внешней среды, при которых развивались особи популяции.
Соотношения между значениями генотипической и средовой варианс могут быть различными. Так если экспериментатор работает с клонами (черенковые саженцы, полученные от одного дерева), то в этом случае генотипическая варианса будет равна нулю, и общая фенотипическая варианса будет состоять только из средового компонента. Если же работа ведется на выровненном экофоне (в абсолютно контролируемых условиях фитотронов) с различным по происхождению материалом, то различия между сравниваемыми объектами будут определяться преимущественно (в идеале полностью) различиями в их генотипах.
Таким образом, получено наиболее общее выражение, характеризующее фенотипическую структуру популяции по количественному признаку. Фенотипическая варианса распадается на два компонента – генотипическую и средовую вариансы. P = G + E
Какими бы путями ни создавалась фенотипическая изменчивость в популяциях, и из каких бы компонентов она ни состояла, она всегда может быть выявлена и измерена вариансой – мерой оценки дисперсии. Самое существенное заключается в выяснении того, какую долю в общей фенотипической вариансе занимает варианса, зависящая от генетических различий между особями в популяции, то есть установлению величины отношения генотипически обусловленной вариансы к общей фенотипической вариансе. Такое отношение принято называть коэффициентом наследуемости.
Коэффициент наследуемости определяется соотношением варианс (дисперсий, средних квадратов отклонений), поскольку из обычных статистических мер рассеивания (дисперсии) только вариансу (s2) можно разложить на компоненты.
С селекционно-генетической точки зрения фенотипическая варианса (оценка степени варьирования) в самом простом случае может быть обусловлена тремя причинами:
1. генотипическими различиями, обусловленными непосредственным действием генов (аддитивный компонент вариансы - 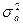 );
);
2. генотипическими различиями, возникающими вследствие межаллельных взаимодействий (компонент вариансы, обусловленный доминированием - 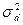 );
);
3. ненаследственными различиями между объектами, вызванными неодинаковым влиянием разнообразных локальных проявлений условий среды (компонент вариансы, обусловленный условиями внешней среды - 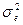 ).
).
Поскольку компоненты вариансы суммируются, общая фенотипическая варианса (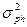 ) представляет их сумму. Общепринята следующая формула её расчета:
) представляет их сумму. Общепринята следующая формула её расчета:
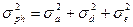

Так как аддитивная генотипическая варианса и неаддитивная генотипическая варианса являются генотипическими компонентами фенотипиеческой (общей) изменчивости, то их можно суммировать и получить генотипически обусловленную вариансу (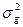 ):
):
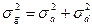
С учетом этого, общая фенотипическая варианса может быть представлена в следующем виде:

Коэффициент наследуемости в широком смысле, основные понятия
Коэффициентом наследуемости – называется отношение генотипической вариансы к общей вариансе.
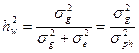
Этот коэффициент наследуемости является коэффициентом наследуемости в широком смысле (учитывает всю генотипически обусловленную долю наследуемости - и аддитивную и неаддитивную вместе). Он содержит в своем расчетном алгоритнме не только стойко наследуемый аддитивный компонент вариансы, но и компонент, обусловленный эффектом диминирования признаков или неаддитивный компонент вариансы, который не наследуется полностью и обусловлен аллельным взаимодействием доминантного и рецессивного генов, находящихся в аллельном состоянии). Это может проявляться и существовать только при наличии в популяциях гетерозиготных генотипов (особей - Аа), что практически всегда наблюдается в популяциях древесных и кустарниковых пород. Гетерозиготные генотипы (Аа) при строгом отборе расщепляются и образуют гомозиготные генотипы по рецессивным аллелям (аа) и по доминантным аллелям (АА). Следовательно, не все потомство проявит признаки исходных гетерозиготных особей, то есть наследование признаков исходных родительских форм будет неполным. Поскольку только часть потомства унаследует признаки исходных гетерозиготных родительских форм (в строгом плане – только гетерозиготные особи потомства будут адекватны родителям), то и наследование считается неполным. Поэтому коэффициент наследуемости (способности передачи наследственных признаков от родителей к потомкам) в широком смысле дает несколько завышенное значение наследуемости. Тем не менее, он широко применяется при селекционной оценке популяций.
ПРИМЕЧАНИЕ
Тем не менее, применение коэффициента наследуемости в широком смысле вполне оправдано с позиций того, что он дает представление об уровне обусловленности признака всеми генетическими причинами – и аддитивным эффектом, и эффектом доминирования, и, естественно, не содержит в своей оценке никаких других элементов, влияющих на формирование фенотипических различий. Он избавлен от учета влияния среды на формирование фенотипического разнообразия.
Из формулы расчета видно, что коэффициент наследуемости может варьировать от 0 (в случае полного отсутствия наследования признаков - 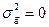 ) до 1 (когда отсутствует средовый компонент обусловленности изменчивости и вся она обусловлена генотипически -
) до 1 (когда отсутствует средовый компонент обусловленности изменчивости и вся она обусловлена генотипически -  ).
).
С теоретической точки зрения главное значение коэффициента наследуемости в широком смысле заключается в том, что он дает возможность устанавливать степень надежности суждений о селекционной ценности особей в популяции по их фенотипической ценности (Рокицкий, 1978, стр. 277-279). Фактически же можно непосредственно судить толь о фенотипических ценностях особей, а селекционные ценности определяются по степени их влияния на следующее поколение. Принимая это условие, мы приходим к выводу о том, что селекционер или экспериментатор, используя коэффициент наследуемости в широком смысле, проводит отбор родителей по их фенотипическим ценностям. Успех же отбора в желательном направлении изменения популяции может быть предсказан только в том случае, если известна степень соответствия между фенотипическими и селекционными значениями. Эта степень соответствия определяется коэффициентом наследуемости в узком смысле.
Естественно, что фенотипические и генотипические значения признаков особей не могут оцениваться абсолютно, а только как отклонения от популяционной средней. Тем не менее, коэффициент наследуемости относится к числу важнейших параметров при генетическом анализе количественных признаков в популяции, его включают почти во все формулы, используемые при селекции растений и животных.
Важно иметь в виду, что наследуемость – это не только характеристика признака, но также и популяции, и тех средовых условиях, в которых находились особи данной популяции.
Так как коэффициент наследуемости вычисляется на основе ряда величин, то изменение в любой из них повлияет на его значение. При дисперсионном анализе и разложении общей фенотипической изменчивости мы составляли достаточно развернутое равенство, правая часть которого включала несколько компонентов: аддитивную вариансу, неаддитивную вариансу, средовую вариансу, а в более подробном изложении еще и вариансу взаимодействия факторов и вариансу вызванную наследственными эффектами помимо аддитивности и доминирования. Все генетические компоненты зависят от частот генов, а по ним разные популяции одного вида организмов могут отличаться в силу своей прошлой истории формирования, в силу тех процессов, которые в них происходили. Поэтому неудивительно, что коэффициенты наследуемости по одному и тому же признаку для разных популяций, кажущихся даже очень сходными, бывают неодинаковы.
ПРИМЕР
Таблица коэффициентов наследуемости в популяциях облепихи по разным признакам.
Так как средовый компонент общей дисперсии признака входит в определение коэффициента наследуемости, то при большой вариации по условиям произрастания (или выращивания) коэффициенты наследуемости будут ниже, а при сравнительно однородных условиях – выше.
ПРИМЕР
Таблица коэффициентов вариации в популяциях облепихи на фоне широты ареала популяции и пестроты условий.
Имеют значения и размеры популяций. Если популяция сравнительно мала, то более вероятны в ней процессы гомозиготизации по ряду генов, отсюда сравнительно низкие показатели наследуемости, чем в более крупных по размерам популяциях
ПРИМЕР
Таблица коэффициентов наследуемости в популяциях облепихи на фоне размеров (численности особей) самих популяций.
Таким образом, обнаруживаемые коэффициенты наследуемости в широком смысле всегда относятся к конкретным популяциям, особи которых находятся в конкретных же условиях произрастания.
*************************
3. Расчет величины коэффициента наследуемости в широком смысле при селекционной оценке популяций.