Представление точек и общая схема преобразования с использованием матриц

Лекция 2. Простые геометрические преобразования на плоскости и в пространстве

Двумерные геометрические (аффинные) преобразования

Представление точек и общая схема преобразования с использованием матриц

Преобразование масштабирования

Преобразование поворота

Преобразование переноса и однородные координаты

Преобразование скоса.

Выполнение произвольных преобразований на плоскости. Композиция преобразований

Выводы по плоским геометрическим преобразованиям

Трехмерные преобразования

Преобразования поворота в пространстве

Коммутативность преобразований в пространстве.

Преобразования как изменение координатных систем

Заключение.

Двумерные геометрические (аффинные) преобразования

В этой лекции мы начинаем изучать математический аппарат машинной графики. В процессе визуализации объекта его необходимо представить в заданном масштабе, повернуть, переместить в требуемую позицию или выполнить другое более сложное преобразование в соответствии с требованиями решаемой задачи. Эти преобразования можно выполнить с помощью рассматриваемого ниже математического аппарата. Для более полного изучения затрагиваемых вопросов вы можете обратиться ко второй редакции книги [5]. Изучение мы начнем с более простых двумерных преобразований, а затем обобщим их, рассмотрев трехмерные преобразования.

Представление точек и общая схема преобразования с использованием матриц

Так как в компьютерной графике большинство объектов определяются с помощью точек или вершин, то начнем именно с них. Как известно, точка на плоскости представляется двумя своими координатами (x y). Эту пару можно представить в виде матрицы [x y] размером 1*2, называемой вектор-строка, или матрицы 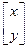размером 2*1, называемой вектор-столбец. Данные матрицы часто называют координатными векторами. В трехмерном пространстве точка определяется тройкой координат, и координатный вектор увеличивает свой размер на единицу. Например, вектор-строка будет иметь размер 1*3 - [x y z].

Правила матричной алгебры определяют набор допустимых операций над координатным вектором.

Если геометрическое преобразование представить в виде матрицы, то результат преобразования точки можно представить следующей формулой:

Р*М = Р’,

где М – матрица геометрического преобразования;

Р – вектор-строка, представляющая исходную точку;

Р’- вектор-строка, полученная в результате преобразования.

Другими словами, мы представили применение геометрического преобразования как произведение матриц. Рассмотрим данное произведение подробнее.

Р*М =[x y] 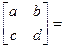[(ax+cy) (bx+dy)] = [x’ y’]

т.е. координаты преобразованной точки формируются суммой исходных координат, умноженных на соответствующие коэффициенты:

x’= ax+cy;

y’= bx+dy;

Если в матрице преобразования a=d=1 и c=b=0 то

x’= 1x + 0y = x;

y’= 0x+1dy = y;

Результат преобразования совпадает с исходными значениями. Матрица 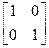- соответствующая такому преобразованию, называется единичной (т.е. квадратная матрица любого размера, главная диагональ которой заполнена единицами). Умножение на такую матрицу подобно умножению на единицу в традиционной алгебре. Несмотря на кажущуюся бесполезность, единичные матрицы находят широкое применение при работе с геометрическими преобразованиями.

В ходе выполнения преобразований нам потребуется решать две задачи. Прямую задачу – находить координаты преобразованного объекта на основе координат исходного объекта и матрицы трансформации. Собственно ее решение рассмотрено нами выше. И обратную задачу – находить координаты исходного объекта на основе координат преобразованного объекта и матрицы трансформации.

Р’* М^-1 = Р,

где М^-1 - это матрица, обратная к матрице трансформации.

Методы получения таких матриц рассматриваются в матричной алгебре. Мы рассмотрим одно важное свойство такой матрицы. Если применить к объекту некоторое преобразование, а затем преобразование, обратное данному, то исходный объект останется неизменным: Р*М* М^-1= Р.

Такой же эффект мы получали при умножении на единичную матрицу. Следовательно, произведение М* М^-1 дает единичную матрицу.