Тема: Неравенства Чебышева. Законы больших чисел Центральная предельная теорема.

Если для неотрицательной случайной величины 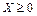существует математическое ожидание 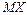, то для всех 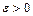выполняется неравенство: 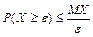(первое неравенство Чебышева).

Если для случайной величины 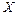существует дисперсия 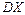, то для всех 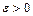выполняется второе неравенство Чебышева: 1) 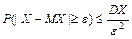(в центрированной форме); 2) 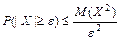(в нецентрированной форме).

Второе неравенство Чебышева часто используют в виде: , .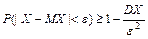

Последовательность случайных величин 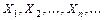называют сходящейся по вероятности к случайной величине 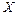(кратко записывается 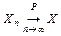), если для всех : .

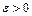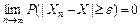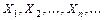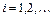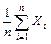
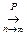
Говорят, что для последовательности случайных величин , имеющих математические ожидания , , выполняется закон больших чисел, если 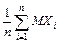, т.е. для всех .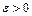

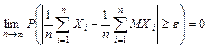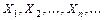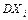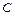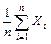
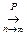
Закон больших чисел в форме Чебышева. Если последовательность независимых случайных величин такова, что существуют и , причём дисперсии этих величин равномерно ограничены (не превышают постоянного числа ), то для неё выполняется закон больших чисел, т.е. 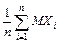. В частности, если случайные величины 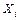, 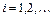являются также одинаково распределёнными (в этом случае 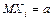, 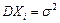), то .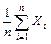

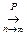
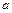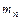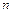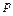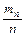
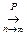
Закон больших чисел в форме Бернулли. Если - число успехов в испытаниях по схеме Бернулли с вероятностью успеха в отдельном испытании, то 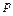, т.е. для всех .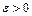

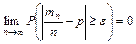Закон больших чисел в форме Бернулли является частным случаем закона больших чисел в форме Чебышева.

Центральная предельная теорема. Пусть 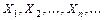- последовательность независимых одинаково распределённых случайных величин (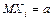, , 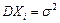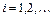), тогда последовательность нормированных случайных величин 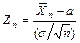, где 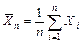, сходится по распределению при к стандартной нормальной величине 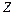~ 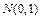, т.е. для всех : .

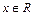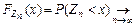
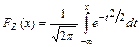12.236 Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор прослужит менее 20 лет.

12.237 Среднее число вызовов, поступающих на станцию скорой помощи в течение часа, равно 30. Оценить вероятности, что в течение следующего часа число вызовов: а) превысит 40; б) будет не более 50.

12.238 Известно, что 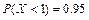. В каких пределах находится 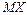, если 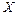- неотрицательная случайная величина?

12.239 Неотрицательные случайные величины 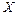и 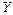независимы. Оценить снизу вероятности событи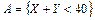й: и 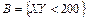, если , .

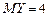12.240 Пусть случайная величина 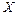- число выпадений герба при 10 подбрасываниях монеты, а случайная величина 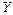- число выпавших очков при одном бросании игральной кости. Оценить снизу вероятность события .

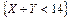12.241 Оценить снизу вероятность того, что отклонение любой случайной величины от её математического ожидания по абсолютной величине будет не более трёх средних квадратичных отклонений (правило трёх сигм).

12.242 Случайная величина 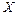имеет числовые характеристики 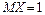, 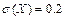. Оценить снизу вероятности следующих событий: