
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление длины гипотенузы по катетам
|
|
Пример 1. Линейный алгоритм
2. Формулировка задания. Даны два вещественных числа, являющихся величинами катетов некоторого прямоугольного треугольника. Вычислить длину гипотенузы этого треугольника.
3. Анализ задачи.
3.1. Входные данные. Входными данными являются длины катетов x и y.
3.2. Результат. Результатом работы алгоритма является вычисленное значение гипотенузы z.
3.3. Формулы. Будем вычислять гипотенузу по формуле Пифагора.
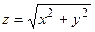
4. Проектирование алгоритма.
В простых задачах, с которыми мы всегда будем иметь дело, единственное действие «полный алгоритм решения задачи» всегда можно заменить последовательностью трех действий. Соответствующая блок-схема изображена на рис 1.
 |
2. Детализируем главный алгоритм. Для этого: напишем входные данные и результат в явном виде.
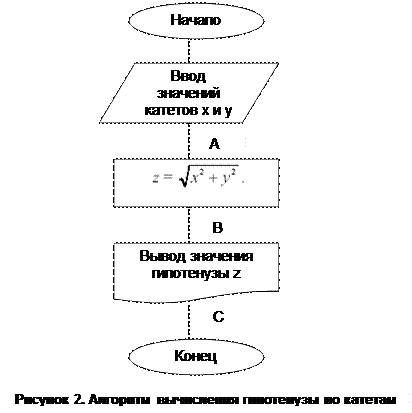
5. Тестирование алгоритма.
Осталось протестировать этот алгоритм вычисления гипотенузы. Расставим на алгоритме контрольные точки A, B, C (см. рис. 2). Контрольные точки ставятся везде, где вводятся или изменяются данные, т. е. после каждого ввода и каждого действия алгоритма (на блок-схеме контрольные точки ставятся после всех параллелограммов и прямоугольников, кроме вывода данных).
Исполнитель начинает выполнять алгоритм с его начала. При движении по алгоритму его активная точка проходит сначала контрольную точку A, затем B, и наконец C.
Зададим входные данные. Пусть катет x = 3, а катет y = 4. Тогда, по формуле Пифагора, гипотенуза такого прямоугольного треугольника должна быть z = 5. Разберем работу алгоритма, представленного на рис. 2. Для этого составим таблицу 1 из значений данных в контрольных точках.
Таблица 1. Тестирование алгоритма вычисления гипотенузы по катетам
| Контрольная точка | Значения данных |
| A | x = 3, y = 4 |
| B | x = 3, y = 4, z = 5 |
| C | x = 3, y = 4, z = 5 |
6. Вывод. Алгоритм вычислил значение гипотенузы z=5, что совпадает с расчетным значением. Поскольку алгоритм простой, то, скорее всего, он работает правильно. Для большей уверенности в правильной работе алгоритма желательно проверить его еще на нескольких более сложных тестах.