
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Погрешности измерений
|
|
Достоверность измерений оценивается погрешностью – отклонением результата измерений от истинного значения измеряемой величины.
Различают абсолютную и относительную погрешности измерений.
Абсолютная погрешность измерений выражается в единицах измеряемой величины и определяется по формуле
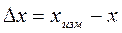 ,
,
где 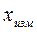 – значение, полученное при измерении;
– значение, полученное при измерении;
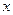 – истинное значение измеряемой величины.
– истинное значение измеряемой величины.
За истинное значение принимается (условно) значение, полученное с помощью эталона или метода (прибора), имеющего точность, превышающую точность применяемого при измерении, в три раза и более.
Относительная погрешность – погрешность, определяемая как отношение абсолютной погрешности к истинному значению измеряемой величины, выраженное в процентах:
 .
.
Приведенная погрешность – отношение абсолютной погрешности к нормирующему значению 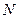 :
:
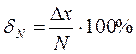 ,
,
где 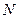 – диапазон измерения прибора.
– диапазон измерения прибора.
Погрешности измерений подразделяются на систематические, случайные и грубые.
Систематические погрешности – составляющие погрешности измерений, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях одной и той же величины.
Систематические погрешности неизбежны, но они могут быть устранены путем введения соответствующих поправок.
Поправка – систематическая ошибка с противоположным знаком.
Прогрессирующие погрешности – погрешности, медленно изменяющиеся в течение времени.
Случайные – неопределенные по своему значению или недостаточно изученные. Их появление не подчиняется какой-либо закономерности.
Процесс появления случайной погрешности – стационарный случайный процесс. Её размер характеризуется указанием закона распределения их вероятностей или указанием параметров этого закона.
Для выявления случайной составляющей погрешности необходимо провести ряд повторных измерений. Определение её осуществляется на основе теории вероятностей и математической статистики.
Эти методы дают возможность оценить вероятные границы погрешностей.
Случайные погрешности, как и большинство случайных величин, подчиняются нормальному закону распределения (закону Гаусса), который характеризуется плотностью вероятностей вида:
 ,
,
где 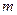 – математическое ожидание измеряемой случайной величины
– математическое ожидание измеряемой случайной величины 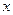 ;
;
 – среднее квадратическое отклонение величины
– среднее квадратическое отклонение величины 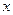 , служащее мерой рассеяния полученных данных относительно среднего значения.
, служащее мерой рассеяния полученных данных относительно среднего значения.
По оси абсцисс (рис. 1.2.1) отложены результаты измерений, ординат – вероятность их появления.
Математическим ожиданием случайной величины 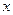 является сумма всех случайных значений, умноженных на вероятность этих значений.
является сумма всех случайных значений, умноженных на вероятность этих значений.

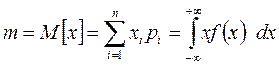 ,
,
где 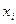 – частные значения измеряемой величины (i = 1, 2, 3…);
– частные значения измеряемой величины (i = 1, 2, 3…);
 – вероятность
– вероятность  -го события
-го события
(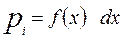 ).
).
| Рис. 1.2.1 |
Математическое ожидание можно определить как среднее арифметическое измеряемых величин:
 .
.
Чем больше 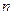 , тем ближе
, тем ближе 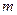 к истинному значению математического ожидания.
к истинному значению математического ожидания.
Если при некоторых условиях должно произойти одно из 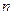 событий, причем ни одно из них нет оснований считать предпочтительнее других, то эти события имеют одинаковую вероятность, равную
событий, причем ни одно из них нет оснований считать предпочтительнее других, то эти события имеют одинаковую вероятность, равную
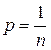 .
.
Если некоторое событие  появляется как следствие какого-либо из
появляется как следствие какого-либо из 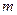 событий при общем числе
событий при общем числе 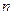 возможных событий, то вероятность вычисляют по формуле
возможных событий, то вероятность вычисляют по формуле
 .
.
Невозможному событию соответствует вероятность 0, достоверному – 1.
Вероятность любого события заключается между 0 и 1. Дисперсия дискретных и непрерывных величин (второй центральный момент) определяется соответственно по формуле

 .
.
Корень квадратный из дисперсии является средним квадратическим или стандартным отклонением (стандартом)  случайной величины
случайной величины 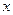 . Его действительное (эффективное) значение и характеризует рассеяние, разбросанность случайной величины около ее математического ожидания.
. Его действительное (эффективное) значение и характеризует рассеяние, разбросанность случайной величины около ее математического ожидания. 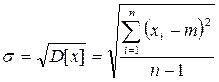 .
.
Если взять интервал погрешностей  и подсчитать интеграл вероятностей, то окажется, что площадь под кривой, ограничиваемая этим интервалом, составляет 68 % всей площади. Это значит, что из всех случаев измерения какой-либо величины 68 % значений будет отклоняться от наиболее вероятного значения (математического ожидания) измеряемой величины не более чем на
и подсчитать интеграл вероятностей, то окажется, что площадь под кривой, ограничиваемая этим интервалом, составляет 68 % всей площади. Это значит, что из всех случаев измерения какой-либо величины 68 % значений будет отклоняться от наиболее вероятного значения (математического ожидания) измеряемой величины не более чем на 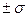 . Если взять за допустимый интервал
. Если взять за допустимый интервал  , то в этом интервале будут находиться 98 % всех измеренных значений. Для интервала
, то в этом интервале будут находиться 98 % всех измеренных значений. Для интервала 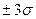 вероятность появления результатов измерений в этом интервале составляет 0, 997. Это означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше
вероятность появления результатов измерений в этом интервале составляет 0, 997. Это означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше 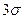 (правило трех сигм). Отсюда понятие доверительного интервала. Доверительным называется интервал, в котором с заданной вероятностью находится истинное значение измеряемой величины. Например, для вероятности (доверительной вероятности) 0, 95 доверительный интервал составит
(правило трех сигм). Отсюда понятие доверительного интервала. Доверительным называется интервал, в котором с заданной вероятностью находится истинное значение измеряемой величины. Например, для вероятности (доверительной вероятности) 0, 95 доверительный интервал составит  . Используют также значения доверительной вероятности 0, 90; 0, 98; 0, 99 и 0, 999.
. Используют также значения доверительной вероятности 0, 90; 0, 98; 0, 99 и 0, 999.
Значение суммы статистически независимых величин безотносительно к разнообразию законов распределения каждой из суммируемых величин:
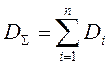 или
или 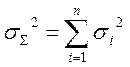 .
.
При косвенных измерениях:
 .
.
Дисперсия величины при условии независимости прямых измерений аргументов 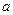 ,
, 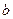 ,
, 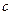 определяется:
определяется:
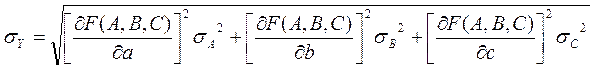 .
.
Вероятность нахождения случайной погрешности в интервале 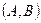 будет определяться выражением:
будет определяться выражением:  .
.
 – функция распределения случайной величины
– функция распределения случайной величины
 .
.
При замене 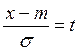
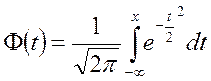 ,
,
при  и
и 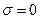
 .
.
В действительности все три составляющие погрешности: систематическая и случайная– проявляются совместно и образуют единый нестационарный случайный процесс.
Число наблюдений 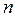 , необходимое для определения доверительного интервала
, необходимое для определения доверительного интервала  с заданной вероятностью
с заданной вероятностью 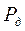 , составит
, составит
 ,
,
где  – количество отбрасываемых с концов ряда наблюдений (табл. 1.2.1).
– количество отбрасываемых с концов ряда наблюдений (табл. 1.2.1).
Таблица 1
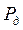
| 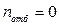
| 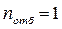
| 
|
| 0, 8 | |||
| 0, 9 | |||
| 0, 95 | |||
| 0, 99 | |||
| 0, 995 | |||
| 0, 997 |
Для определения  с
с 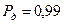 или
или 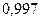 необходимо выполнить
необходимо выполнить 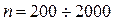 .
.
Тем не менее в практике по небольшой серии измерений (20-30) вычисляют среднеквадратическую погрешность  , а затем указывают максимальную погрешность
, а затем указывают максимальную погрешность 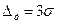 , с доверительной вероятностью 0, 997 на основании предположения о нормальном законе распределения.
, с доверительной вероятностью 0, 997 на основании предположения о нормальном законе распределения.
Для обобщенной оценки погрешности приборов контроля состава пищевых продуктов используют статистические методы обработки измерительной информации. Основными метрологическими характеристиками для оценки точности приборов являются среднеквадратическое отклонение  показаний прибора от данных измерений контрольным методом, систематическое отклонение
показаний прибора от данных измерений контрольным методом, систематическое отклонение 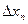 , а также сходимость показаний
, а также сходимость показаний 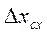 :
:
 ,
,
где 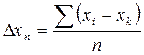 ;
;
 – значение параметра, измеряемого прибором;
– значение параметра, измеряемого прибором;
 – значение параметра, измеряемого контрольным прибором;
– значение параметра, измеряемого контрольным прибором;
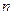 – число проб (
– число проб ( ).
).
Предельная погрешность составляет  .
.
При доверительной вероятности 0, 95 для биологических объектов 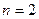 . Сходимость показаний
. Сходимость показаний 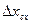 определяют по результатам
определяют по результатам 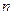 измерений (
измерений (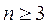 ):
):
 ,
,
где  –среднее из
–среднее из 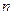 измерений.
измерений.
Анализ дезинформационного действия случайных помех с различными законами распределения вероятностей показал, что вносимая помехой дезинформация определяется не только мощностью этой помехи ( ), но еще зависит и от вида закона распределения этой помехи.
), но еще зависит и от вида закона распределения этой помехи.
Если помеха в вероятностном смысле не зависит от сигнала, то для любого закона распределения и мощности сигнала дезинформационное действие помехи определяется ее энтропией:
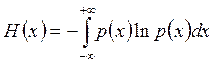 ,
,
где 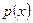 – плотность распределения.
– плотность распределения.
Энтропийный коэффициент
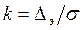 .
.
Для нормального закона распределения:
 .
.
Практически используемая оценка погрешности в виде максимального значения из серии 2-х наблюдений наиболее близка именно к энтропийному значению погрешности.
Использование энтропийного значения погрешности  и энтропийного коэффициента k в законе распределения позволит получить простую и строгую связь мощности помехи с дезинформацией
и энтропийного коэффициента k в законе распределения позволит получить простую и строгую связь мощности помехи с дезинформацией  или с получаемым при измерении количеством информации
или с получаемым при измерении количеством информации 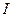 в виде
в виде
 .
.
Грубые погрешности (промахи) – составляющая, существенно превышающая ожидающую, – как правило, отбрасываются и не учитываются.
Точность измерений отражает близость результатов измерений к истинному значению. Количественно точность измерений выражается величиной, обратной модулю относительной погрешности:
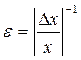 .
.
Правильность измерения – близость к нулю систематических погрешностей.
Сходимость измерений – близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Воспроизводимость – близость друг к другу результатов измерений, выполненных в различных условиях.
Погрешность измерений определяется погрешностью средства измерения, применяемым методом, свойствами измеряемой величины и условиями, в которых производятся измерения.
Погрешность средства измерения – свойство собственно средства, которое описывается совокупностью нормированных метрологических характеристик.
Разность между показаниями прибора и истинным значением измеряемой величины называется абсолютной погрешностью измерительного прибора и определяется по формуле:
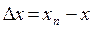 ,
,
где 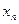 – показания прибора;
– показания прибора;
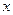 – истинное значение измеряемой величины.
– истинное значение измеряемой величины.
Одна из характеристик точности прибора – относительная погрешность, определяемая как отношение абсолютной погрешности к показаниям измерительного прибора
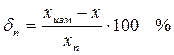 .
.
Основная погрешность – погрешность средства, используемого в нормальных условиях (определяемых ГОСТом или техническими условиями).
Дополнительная погрешность – погрешность, вызванная отклонением от нормальных условий эксплуатации (температура, вибрация, перекос). От величины основных и дополнительных погрешностей зависит класс точности средства измерений – обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей.
Классы точности выбираются из ряда следующих чисел: 1; 1, 5; 2; 2, 5; 4; 5; 6; 10, где n=1; 0; -1; -2 и т.д.
Качество измерений характеризуется также правильностью и сходимостью показаний средств измерений.