
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статические и динамические характеристики средств измерений
|
|
Работа средств измерений характеризуется функцией преобразования, общий вид которой
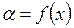 .
.
При анализе сложной измерительной цепи средство измерений может быть разделено на ряд звеньев.
Функция преобразования является обобщенной характеристикой измерительной цепи, так как связывает между собой входную и выходную величины.
Статическая функция преобразования определяет свойства измерительной цепи в установившемся состоянии.
В условиях меняющейся входной величины проявляются динамические свойства средств измерения, которые определяют поведение цепи или ее элементов в переходных режимах, а также при воздействии на вход переменных, в частном случае, периодических воздействий. Эти свойства описываются динамическими характеристиками.
Идеальной статической функцией преобразования можно считать линейную:
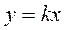 .
.
Эту функцию характеризуют чувствительность и диапазон преобразования. Чувствительность или коэффициент преобразования 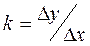 . Диапазон преобразования – область входных величин, в пределах которой элемент или измерительная цепь обеспечивает реализацию функции преобразования. Он ограничивается верхним и нижним пределом. В общем случае функция преобразования имеет вид:
. Диапазон преобразования – область входных величин, в пределах которой элемент или измерительная цепь обеспечивает реализацию функции преобразования. Он ограничивается верхним и нижним пределом. В общем случае функция преобразования имеет вид:
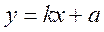 .
.
Дефекты статической функции преобразования являются источниками погрешностей средств измерения. К ним относят: нелинейность, гистерезис, порог чувствительности, дрейф нуля.
§ Нелинейность характеризует несоответствие фактической функции преобразования и идеальной модели.
Относительная приведенная нелинейность оценивается отношением максимальной разности 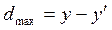 к диапазону преобразования
к диапазону преобразования 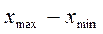 :
:
 . (1.3.1)
. (1.3.1)
§ Гистерезис – неоднозначность функции преобразования при увеличении и уменьшении входной величины. В пределах зоны, ограниченной ветвями характеристики, средство измерения теряет чувствительность.
Относительное приведенное значение гистерезиса:
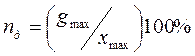 . (1.3.2)
. (1.3.2)
|
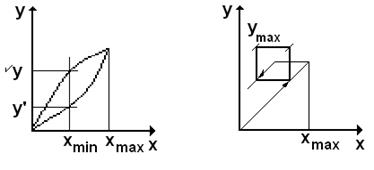
§ Порог чувствительности – минимальное изменение входной величины, вызывающее заметное изменение выходной:
| Рис. 1.3.1 |
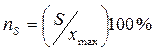 . (1.3.3)
. (1.3.3)
§ Дрейф нуля – смещение функции преобразователя.
Динамический элемент, имеющий характеристику вида 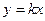 , называется усилительным или пропорциональным. Это идеальная динамическая характеристика.
, называется усилительным или пропорциональным. Это идеальная динамическая характеристика.
Реальные средства измерения вносят в измеряемую величину динамические искажения.
Динамические характеристики могут представляться в виде переходных и частотных характеристик и передаточных функций.
§ Переходная характеристика – значения выходной величины во времени при изменении входной величины по заранее известному закону (ступенчатая функция):
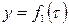 при
при  ,
,
где 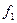 – искомая функция;
– искомая функция;
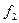 – известная функция.
– известная функция.
Переходную характеристику получают путем решения дифференциальных уравнений или экспериментально.
§ Частотные характеристики представляют зависимость амплитуды и фазы выходной величины от частоты входного гармонического сигнала:
на входе: 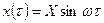 ;
;
на выходе: 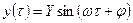 .
.
В комплексном виде:
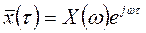 ;
; 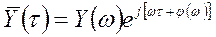 , (1.3.4)
, (1.3.4)
где 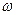 – угловая частота;
– угловая частота;
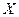 и
и 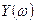 – модули векторов
– модули векторов  и
и 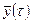 ;
;
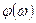 – угол сдвига фаз.
– угол сдвига фаз.
Выражение 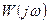 называют комплексной частотной характеристикой (КЧХ):
называют комплексной частотной характеристикой (КЧХ):
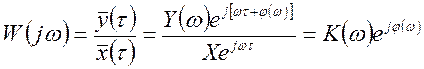 . (1.3.5)
. (1.3.5)
Функции  и
и 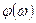 – амплитудно-частотная и фазочастотная характеристики. В ряде случаев используют логарифмические амплитудно-частотные характеристики (ЛАЧХ):
– амплитудно-частотная и фазочастотная характеристики. В ряде случаев используют логарифмические амплитудно-частотные характеристики (ЛАЧХ):  . Величина
. Величина 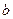 называется затуханием и выражается в децибелах (дБ).
называется затуханием и выражается в децибелах (дБ).
§ Передаточная функция – обобщенный вид динамической характеристики, представляющий собой отношение преобразованных по Лапласу выходного и входного сигналов.
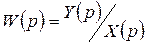 , (1.3.6)
, (1.3.6)
где р–комплексное выражение из преобразования Лапласа.
Передаточная функция определяется путем анализа дифференциальных уравнений, а также по таблицам типовых функций.
Примером апериодического элемента 1-го порядка может служить термопреобразователь сопротивления. Сопротивление при температуре 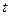 :
:
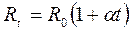 ,
,
где 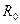 – сопротивление при температуре 0 °С;
– сопротивление при температуре 0 °С;
 – термический коэффициент сопротивления материала.
– термический коэффициент сопротивления материала.
Статическая характеристика проходит через точку (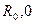 ). При скачкообразном изменении температуры среды от
). При скачкообразном изменении температуры среды от 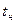 до
до 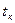 процесс изменения
процесс изменения 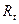 во времени будет описываться выражением
во времени будет описываться выражением
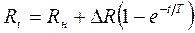 , (1.3.7)
, (1.3.7)
где 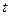 – время от момента
– время от момента 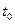 , с;
, с;
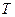 – постоянная времени, характеризующая скорость протекания процесса,
– постоянная времени, характеризующая скорость протекания процесса,  (
( – теплоемкость преобразования, Дж/°С;
– теплоемкость преобразования, Дж/°С;  – произведение коэффициента теплопередачи на площадь поверхности, Вт/м
– произведение коэффициента теплопередачи на площадь поверхности, Вт/м  .°С);
.°С);
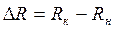 (
(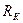 – конечное значение сопротивления, Ом;
– конечное значение сопротивления, Ом; 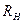 – начальное значение сопротивления, Ом).
– начальное значение сопротивления, Ом).
Численно постоянная времени равна отрезку времени от момента скачка до момента, когда величина 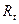 пройдет 63 %
пройдет 63 % 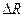 .
.
При помещении термопреобразователя в различные среды можно получить различные значения постоянной времени в зависимости от коэффициента теплоотдачи.
При использовании времени 99-го приближения (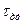 ) постоянная времени:
) постоянная времени:  .
.
При изменении температуры по синусоидальному закону
 .
.
Сопротивление составит:
 ;
; 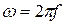 ;
; 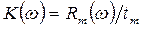 ,
,
где  и
и 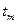 – амплитудные значения сопротивления и температуры;
– амплитудные значения сопротивления и температуры;
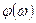 - фазочастотная характеристика (ФЧХ);
- фазочастотная характеристика (ФЧХ);
 - амплитудно-частoтнaя характеристика (АЧХ).
- амплитудно-частoтнaя характеристика (АЧХ).
Частота, при которой 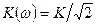 , а
, а 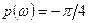 , называется граничной
, называется граничной
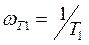 ;
;  ;
;  ,
,
где 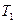 ,
,  ,
, 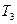 - постоянные времени.
- постоянные времени.
Амплитудно-фазовые характеристики (АФХ) могут быть найдены аналитически:
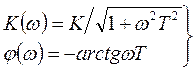 . (1.3.8)
. (1.3.8)
Передаточная функция, апериодического элемента 1-го порядка определяется по формуле:
 . (1.3.9)
. (1.3.9)
Пусть термометром с постоянной времени 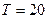 °С измеряют две температуры (t1 и t2), перенося термометр из одного сосуда в другой. Определим время, в течение которого показания термометра tтм не будут отличаться от измеряемой температуры более чем на 0, 1 °С, т.е.
°С измеряют две температуры (t1 и t2), перенося термометр из одного сосуда в другой. Определим время, в течение которого показания термометра tтм не будут отличаться от измеряемой температуры более чем на 0, 1 °С, т.е.  °С.
°С.
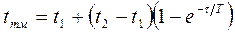 ;
;  °С;
°С;  °С;
°С;
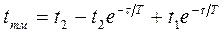 ;
;
 ;
; 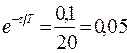 ;
;
 ;
;  с.
с.
Таким образом, отсчет температуры необходимо производить через 106 с после переноса термометра.
Примером колебательного элемента может служить металлическая мембрана, жестко закрепленная по периметру. Отличительной особенностью такого элемента являются свободные колебания.
Амплитудно-частотную характеристику можно представить в виде:
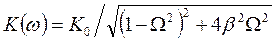 , (1.3.10)
, (1.3.10)
где 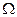 – относительная частота,
– относительная частота, 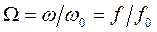 (
( – собственная угловая частота свободных колебаний);
– собственная угловая частота свободных колебаний);
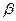 – степень успокоения или относительное затухание.
– степень успокоения или относительное затухание.
При резонансе амплитуда резко возрастает. Если обозначить 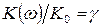 , то можно определить максимальную частоту сигнала, при которой повышение амплитуды будет не больше заданной:
, то можно определить максимальную частоту сигнала, при которой повышение амплитуды будет не больше заданной:
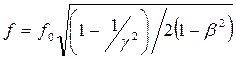 . (1.3.11)
. (1.3.11)
Из теории известно, что при 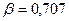 амплитудно-частотная характеристика не имеет резонансного подъема и, с точки зрения воспроизведения сигнала, является наиболее благоприятной.
амплитудно-частотная характеристика не имеет резонансного подъема и, с точки зрения воспроизведения сигнала, является наиболее благоприятной.
Пусть собственная частота свободных колебаний мембраны  кГц, относительное затухание
кГц, относительное затухание 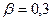 . Предельная частота синусоидальных колебаний давления, при которой резонансный подъем превышает коэффициент передачи при нулевой частоте не более чем на 10 %, то-есть
. Предельная частота синусоидальных колебаний давления, при которой резонансный подъем превышает коэффициент передачи при нулевой частоте не более чем на 10 %, то-есть 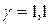 , составит:
, составит:
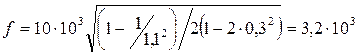 Гц.
Гц.
В качестве дифференцирующего элемента может быть рассмотрен преобразователь давления с пьезоэлектрическим чувствительным элементом.
В идеальном дифференцирующем элементе скачкообразное входное воздействие вызывает появление на выходе импульса напряжения бесконечно большой высоты и бесконечно малой длительности.
Передаточная функция реального дифференцирующего элемента:
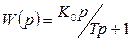 . (1.3.12)
. (1.3.12)
Амплитудно-частотная характеристика:
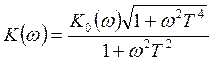 . (1.3.13)
. (1.3.13)
Примером элемента чистого запаздывания. может служить соединительный канал между источником давления и входом преобразователя.
Передаточная функция может быть представлена в виде:
 . (1.3.14)
. (1.3.14)
Общая передаточная функция при последовательном соединении элементов измерительной цепи определяется как произведение передаточных функций отдельных элементов:
 (1.3.15)
(1.3.15)
При параллельном включении – как сумма:
 . (1.3.16)
. (1.3.16)
Основные понятия о надежности средств измерений
Надежность средств измерений – их способность сохранять заданные характеристики при определенных условиях работы в течение заданного времени.
Если задание одной или нескольких характеристик средств измерений выходит из заданных предельных значений, то говорят, что имеет место отказ. Количественной мерой надежности является время безотказной работы средств измерений в заданных промежутках времени и условиях работы. Вероятностью безотказной работы называется вероятность того, что в течение определенного времени  непрерывной работы не произойдет ни одного отказа.
непрерывной работы не произойдет ни одного отказа.
К показателям надежности относят также среднее время безотказной работы средств измерений, которое определяется как среднее арифметическое времени непрерывной работы.
Вероятность безотказной работы определяется из следующего выражения:
 , (1.4.1)
, (1.4.1)
где  – функция распределения времени безотказной работы, которая представляет собой вероятность появления отказа в течение времени
– функция распределения времени безотказной работы, которая представляет собой вероятность появления отказа в течение времени  .
.
 ;
;  ;
; 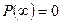 .
.
где  – монотонно убывающая функция;
– монотонно убывающая функция;
 – монотонно возрастающая функция.
– монотонно возрастающая функция.
Статистическая оценка вероятности безотказной работы определяется из следующего выражения:
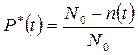 , (1.4.2)
, (1.4.2)
где 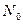 – число изделий, поставленных на испытания;
– число изделий, поставленных на испытания;
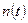 – число изделий, отказавших в течение времени
– число изделий, отказавших в течение времени 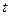 .
.
Частота отказов – плотность распределения времени безотказной работы или производная от вероятности безотказной работы:
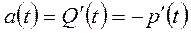 . (1.4.3)
. (1.4.3)
Таким образом,
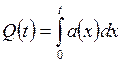 ;
; 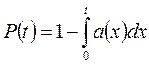 .
.
Статистическая оценка частоты отказов:
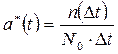 , (1.4.4)
, (1.4.4)
где n( 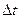 ) – число отказавших изделий за время
) – число отказавших изделий за время 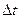 .
.
Интенсивность отказов представляет собой условную плотность распределения времени безотказной работы для момента времени 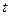 при условии, что до момента времени
при условии, что до момента времени 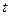 отказ устройства не произошел.
отказ устройства не произошел.
Интенсивность отказов определяется из выражения:
 ;
;  ; (1.4.5)
; (1.4.5)
Статистическая оценка интенсивности отказов:
 ;
; 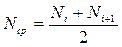 , (1.4.6)
, (1.4.6)
где 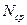 – среднее число исправно работающих изделий за время
– среднее число исправно работающих изделий за время 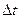 .
.
Интегрируя  , получим:
, получим:
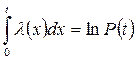 или
или  .
.
Если 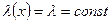 , то
, то 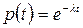 и
и 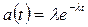 .
.
Средняя наработка до отказа – математическое ожидание наработки до первого отказа:
 ;
;
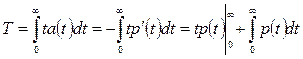 ;
;

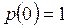 и
и 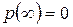 ;
;
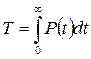 .
.
Для экспоненциального закона распределения:
 . (1.4.7)
. (1.4.7)
Статистическая оценка средней наработки до отказа:  . (1.4.8)
. (1.4.8)
Время между соседними отказами для элементов аппаратуры является непрерывной случайной величиной, которая характеризуется некоторым законом распределения.
В большинстве случаев для количественной оценки показателей надежности пользуются экспоненциальным законом.
Вероятность появления отказа в течение времени 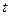 :
:
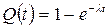 ,
,
где  – параметр экспоненциального распределения.
– параметр экспоненциального распределения.
Вероятность безотказной работы:
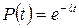 .
.
Частота отказов: 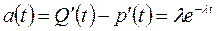 .
.
Среднее время безотказной работы: 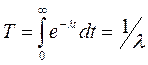 .
.
Дисперсия времени безотказной работы:
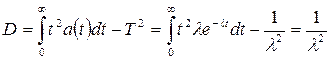 .
.
Если  , то
, то 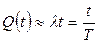 и
и 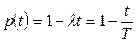 .
.
Для распределения Релея:
 ;
;  ;
;
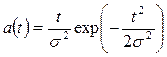 ,
,
где  – параметр распределения Релея.
– параметр распределения Релея.
Среднее время безотказной работы:
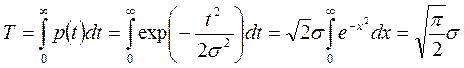 .
.
Дисперсия времени безотказной работы:
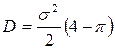 ;
;  .
.