
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциальные уравнения
|
|
Правила и формулы дифференцирования
1) 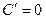 ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) 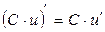 ;
;
6) 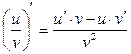 ;
;
7) 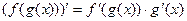
1. 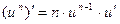
2. 
3. 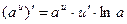
4. 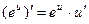
5. 
6. 
7. 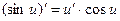
8. 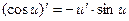
9. 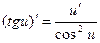
10. 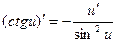
11. 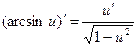
12. 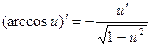
13. 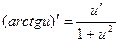
14. 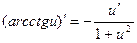
Таблица интегралов
1) 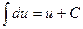
2) 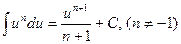
3) 
4) 
5) 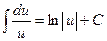
6) 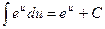
7) 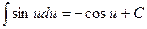
8) 
9) 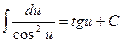
10) 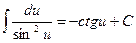
11) 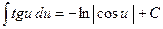
12) 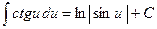
13) 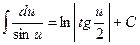
14) 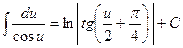
15) 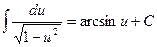
16) 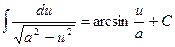
17) 
18) 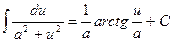
19) 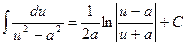
20) 
21) 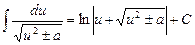
22) 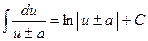
Дифференциальные уравнения
| Вид ДУ | Название | Способ решения |
| ДУ первого порядка | ||
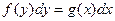
| С разделенными переменными | Интегрирование обеих частей равенства |

| С разделяющимися переменными | «Разделяй и интегрируй» |
 , , 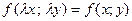
| Однородное | Подстановка 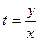 , , 
|

| Линейное неоднородное | Метод Бернулли: 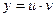 , , 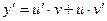
|
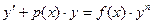 , ,
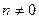 , , 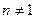
| Уравнение Бернулли | Метод Бернулли:
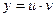 , , 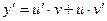
|
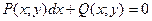 , , 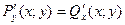
| В полных дифференциалах | 
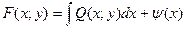
|
| ДУ, допускающие понижение порядка | ||
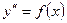
| Не содержащее 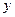 и и 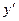
| Двукратное интегрирование |
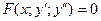
| Не содержащее 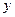
| Подстановка 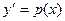 , , 
|
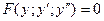
| Не содержащее 
| Подстановка 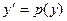 , , 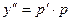
|
| ДУ второго порядка | ||

| ЛОДУ с постоянными коэффициентами | С помощью характеристического уравнения  :
а) :
а) 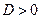 : : 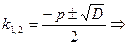 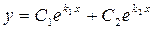 ;
б) ;
б) 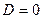 : : 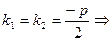 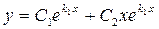 ;
в) ;
в)  : : 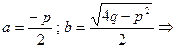 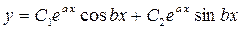 ; ;
|
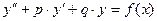
| ЛНДУ с постоянными коэффициентами и правой частью специального вида | 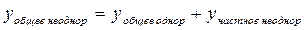 I.
I. 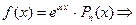 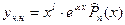 II.
II.  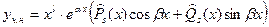
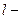 число совпадений число совпадений  с корнями характеристического уравнения; с корнями характеристического уравнения;
 ; ;
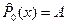 ; ; 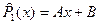 ; ; 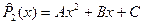 - многочлены с неопределенными коэффициентами - многочлены с неопределенными коэффициентами
|
Ряды
Эталонные ряды: 1) 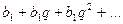 - ряд геометрической прогрессии;
- ряд геометрической прогрессии;
расходится при  ; сходится при
; сходится при 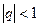 и
и 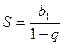 - сумма ряда.
- сумма ряда.
2) 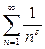 - обобщенный гармонический ряд; расходится при
- обобщенный гармонический ряд; расходится при 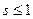 ; сходится при
; сходится при 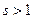 .
.
Признаки сходимости знакоположительных рядов  :
:
1) Первый признак сравнения. Если  , то из сходимости ряда
, то из сходимости ряда 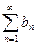 следует сходимость ряда
следует сходимость ряда  ; из расходимости ряда
; из расходимости ряда  следует сходимость ряда
следует сходимость ряда 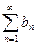 .
.
2) Второй (предельный) признак сравнения. Если  , то ряды
, то ряды  и
и 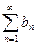 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
3) Признак Даламбера. Если 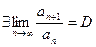 , то при:
, то при:
а) 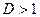 - ряд расходится; б)
- ряд расходится; б) 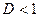 - сходится; в)
- сходится; в) 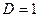 - признак не работает.
- признак не работает.
4) Радикальный признак Коши. Если 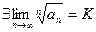 , то при:
, то при:
а) 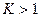 - ряд расходится; б)
- ряд расходится; б) 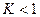 - сходится; в)
- сходится; в) 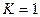 - признак не работает.
- признак не работает.
5) Интегральный признак Коши. Пусть 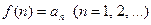 . Тогда ряд
. Тогда ряд  сходится, если сходится интеграл
сходится, если сходится интеграл 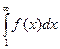 , и расходится в противном случае.
, и расходится в противном случае.
Признак Лейбница: Если  , то
, то 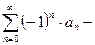 сходится.
сходится.
Степенные ряды: 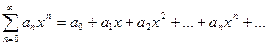 – сходится абсолютно при
– сходится абсолютно при 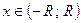 ,
, 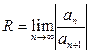 - радиус; расходится при
- радиус; расходится при 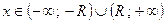 .
.
Ряд Тейлора: 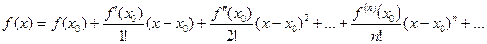
Ряд Маклорена: 
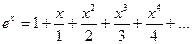 сходится при всех значениях х;
сходится при всех значениях х;
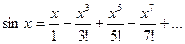 сходится при всех значениях х;
сходится при всех значениях х;
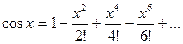 сходится при всех значениях х;
сходится при всех значениях х;
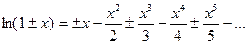 сходится при
сходится при  .
.