
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткая теория. Удаленные друг от друга точечные электрические заряды взаимодействуют по закону Кулона с силой:
|
|
Удаленные друг от друга точечные электрические заряды взаимодействуют по закону Кулона с силой:
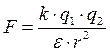 , (1.1)
, (1.1)
где k = 9 × 109 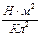 - коэффициент пропорциональности, который можно определить по формуле
- коэффициент пропорциональности, который можно определить по формуле 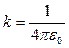 , e0 - электрическая постоянная, равная 8, 85 × 10-12
, e0 - электрическая постоянная, равная 8, 85 × 10-12 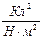 , q1 и q2 - точечные заряды, находящиеся на расстоянии r друг от друга.
, q1 и q2 - точечные заряды, находящиеся на расстоянии r друг от друга.
Точечным зарядом q называется наэлектризованное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует, e - диэлектрическая проницаемость среды, равная отношению силы взаимодействия между зарядами в отсутствии среды F0 и при ее наличии F.
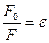 . .
| (1.2) |
Каким же образом осуществляется это взаимодействие при отсутствии вещества между зарядами? Взаимодействие между зарядами происходит через посредство электрического поля. Электрическое поле, образованное системой неподвижных зарядов называется электростатическим.
Для замкнутой системы справедлив закон сохранения электрического заряда - алгебраическая сумма электрических зарядов в замкнутой системе остается постоянной: 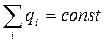 .
.
Если рассмотреть заряд q как «источник» электрического поля, в которое на расстоянии  помещен пробный заряд
помещен пробный заряд 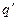 , то на него будет действовать сила:
, то на него будет действовать сила:
 , (1.3)
, (1.3)
где  - радиус вектор, проведенный от заряда
- радиус вектор, проведенный от заряда  к заряду
к заряду 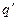 .
.
Отсюда видно, что сила зависит от величины пробного заряда q’: F~ q’. С другой стороны,  не зависит от q’, а зависит от величины заряда q, свойств среды e и положения в пространстве той точки, в которой изучается поле - значения радиус-вектора
не зависит от q’, а зависит от величины заряда q, свойств среды e и положения в пространстве той точки, в которой изучается поле - значения радиус-вектора  . Эту величину можно принять для количественной характеристики электрического поля:
. Эту величину можно принять для количественной характеристики электрического поля:
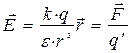 . (1.4)
. (1.4)
Вектор  носит название вектора напряженности электрического поля и служит его силовой характеристикой. В СИ
носит название вектора напряженности электрического поля и служит его силовой характеристикой. В СИ  измеряется в В/м.
измеряется в В/м.
Вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.
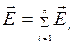 .
.
Это утверждение называется принципом суперпозиции (наложения) электрических полей.
Графически электрическое поле можно показать с помощью силовых линий. Эти линии проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором  в той же самой точке (рис.1.1).
в той же самой точке (рис.1.1).
 Условно принимают, что число линий, проходящих через единичную площадку, ориентированную перпендикулярно этим линиям, должно равняться численной величине Е в данной области поля. Свойство линий напряженности начинаться или заканчиваться только на электрических зарядах или уходить в бесконечность, сохраняется и для полей, создаваемых любой системой электрических зарядов. В качестве примера использования принципа суперпозиции электрических полей рассмотрим поле электрического диполя. Диполем называется совокупность двух одинаковых по абсолютной величине разноименных зарядов + q и - q, расположенных на расстоянии l друг от друга, которое мало по сравнению с расстоянием r от центра диполя О до точки М, в которой определяется напряженность
Условно принимают, что число линий, проходящих через единичную площадку, ориентированную перпендикулярно этим линиям, должно равняться численной величине Е в данной области поля. Свойство линий напряженности начинаться или заканчиваться только на электрических зарядах или уходить в бесконечность, сохраняется и для полей, создаваемых любой системой электрических зарядов. В качестве примера использования принципа суперпозиции электрических полей рассмотрим поле электрического диполя. Диполем называется совокупность двух одинаковых по абсолютной величине разноименных зарядов + q и - q, расположенных на расстоянии l друг от друга, которое мало по сравнению с расстоянием r от центра диполя О до точки М, в которой определяется напряженность  (рис.1.2.).
(рис.1.2.).
Соединим точку наблюдения М с обоими зарядами радиус-векторами 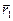 и
и  , проведенными из тех точек, в которых находятся эти заряды. Тогда, вектор напряженности
, проведенными из тех точек, в которых находятся эти заряды. Тогда, вектор напряженности 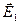 создаваемый зарядом - q в точке М, будет направлен против радиус-вектора
создаваемый зарядом - q в точке М, будет направлен против радиус-вектора 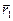 , а
, а 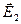 будет направлен по
будет направлен по  . Векторы
. Векторы 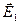 и
и 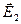 определяются по формуле (1.4), а полный вектор напряженности электрического поля в точке М равен их геометрической сумме:
определяются по формуле (1.4), а полный вектор напряженности электрического поля в точке М равен их геометрической сумме:
 . (1.5)
. (1.5)

|
Из треугольника ОLM на рисунке видно, что вектор  является геометрической суммой вектора
является геометрической суммой вектора  и вектора
и вектора  , где
, где 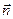 - единичный вектор, направленный вдоль прямой, соединяющей заряды
- единичный вектор, направленный вдоль прямой, соединяющей заряды  и -
и -  . Отсюда
. Отсюда 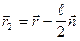 и аналогично
и аналогично  . (1.6) Опуская из точки L перпендикуляр на радиус вектор
. (1.6) Опуская из точки L перпендикуляр на радиус вектор  , мы видим, что величина
, мы видим, что величина
r = ON + NM = 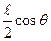 + NM.
+ NM.
Используя условие l < < r, мы можем считать в прямоугольном треугольнике LNM катет NM равным гипотенузе  ; тогда
; тогда
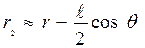 и
и  . (1.7)
. (1.7)
Подставляя (1.7) в (1.5), получаем:
 . (1.8)
. (1.8)
Раскрывая скобки в знаменателях по формуле бинома Ньютона и отбрасывая члены, содержащие малые порядки l2 и l3, имеем:
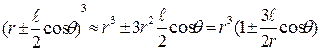 .
.
Воспользуемся правилом приближенного деления, согласно которому при относительной ошибке d < < 1 c точностью до членов второго порядка
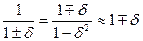 .
.
Тогда
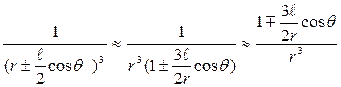 . (1.9)
. (1.9)
Подставляя (1.9) в (1.8) и раскрывая скобки, получим:
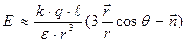 . (1.10)
. (1.10)
Отсюда видно, что напряженность поля диполя определяется не в отдельности величиной зарядов q и расстоянием между ними l, а произведением
p = ql, (1.11)
которое называется дипольным моментом. Поскольку ось диполя ориентирована в пространстве, то дипольный момент является вектором 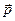 . Он направлен вдоль оси диполя от отрицательного заряда к положительному, т.е. по единичному вектору
. Он направлен вдоль оси диполя от отрицательного заряда к положительному, т.е. по единичному вектору 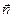 . Следовательно,
. Следовательно,
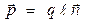 . (1.12)
. (1.12)
Подставляя (1.11) и (1.12) в (1.10), получаем
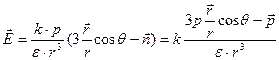 . (1.13)
. (1.13)
Значит, напряженность электрического поля диполя Е прямо пропорциональна величине дипольного момента p и в любом направлении (для любых q) убывает с ростом r как 1/r3.
Рассмотрим точку N, лежащую справа от заряда + q на продолжении оси диполя (рис.1.3.).
|

Для этой точки q = 0, cosq = 1,
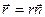 и
и 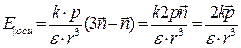 . (1.14)
. (1.14)
Это соотношение остается справедливым и для точек, лежащих на оси диполя слева, где
q = p, cosq = -1, но  .
.
Для точки М, лежащей на перпендикуляре к оси диполя, q = p / 2, cosq = 0 и
 . (1.15)
. (1.15)
Для произвольного q, возводя выражение (1.13) в квадрат и принимая во внимание, что скалярное произведение 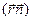 равно r cosq, можно легко вычислить величину вектора
равно r cosq, можно легко вычислить величину вектора  :
:
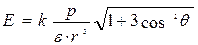 . (1.16)
. (1.16)
Теорема Остроградского-Гаусса
Потоком вектора напряженности электрического поля сквозь малый участок поверхности, проведенной в поле, называется величина
dN = E dS cos (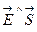 )=
)=  . (1.17)
. (1.17)
где  - вектор напряженности электрического поля в точках малого участка поверхности площадью dS,
- вектор напряженности электрического поля в точках малого участка поверхности площадью dS, 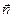 - единичный вектор, нормальный к площадке dS, а вектор
- единичный вектор, нормальный к площадке dS, а вектор  .
.
dN = EndS = EdS^. (1.18)
Поток напряженности N сквозь любую поверхность S равен алгебраической сумме потоков напряженности сквозь все малые участки этой поверхности:
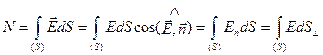 . (1.19)
. (1.19)
При этом все векторы 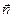 нормалей к малым площадкам dS нужно направлять в одну и ту же сторону относительно поверхности S.
нормалей к малым площадкам dS нужно направлять в одну и ту же сторону относительно поверхности S.
Рассмотрим электростатическое поле системы точечных зарядов q1, q2,..., qn. Согласно принципу суперпозиции полей:
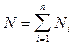 , (1.20)
, (1.20)
т.е. искомый поток N равен алгебраической сумме потоков через ту же замкнутую поверхность S напряженности полей каждого из зарядов системы. Поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической сумме электрических зарядов, охватываемых этой поверхностью, к электрической постоянной e0.
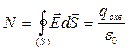 . (1.21)
. (1.21)
Рассмотрим несколько примеров использования теоремы Остроградского-Гаусса.