
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бесконечно заряженная плоскость
|
|
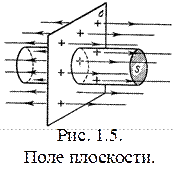 Рассмотрим равномерно заряженную бесконечную плоскость с постоянной поверхностной плотностью заряда s:
Рассмотрим равномерно заряженную бесконечную плоскость с постоянной поверхностной плотностью заряда s:
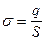 - это заряд, распределенный по площади S.
- это заряд, распределенный по площади S.
Вектор электрического поля будет направлен нормально от плоскости, если s> 0.
Для определения модуля вектора напряженности, создаваемого пластиной, применим теорему Гаусса к замкнутой цилиндрической поверхности (рис. 1.5). Ось цилиндра перпендикулярна заряженной плоскости, и последняя делит высоту цилиндра пополам. Оба основания параллельны заряженной плоскости и имеют одинаковую площадь S.
Поток вектора напряженности через цилиндрическую поверхность равен:
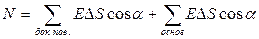 (1.23)
(1.23)
На боковой поверхности вектор E параллелен поверхности и cosα = 0. На торцах цилиндра вектор E перпендикулярен поверхности и cosα = 1, а величина E одинакова на обоих основаниях; следовательно,

 (1.24)
(1.24)
Проведенная цилиндрическая поверхность вырезает из плоскости такую же площадку S c полным зарядом:
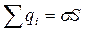 (1.25)
(1.25)
Подставляя (1.24) и (1.25) в левую и правую части (1.21) получаем:
откуда
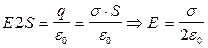 (1.26)
(1.26)