
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вероятностный смысл математического ожидания
|
|
Пусть произведено п испытаний, в которых случайная величина X приняла т1 раз значение х1, т2 раз значение х2,..., тк раз значение хк, причем m1+m2+...+ mk = n. Тогда сумма всех значений, принятых X, равна
x1m1 + x2m2 + … + xkmk.
Найдем среднее арифметическое X всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний:
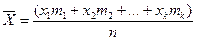
или

Заметив, что отношение m1/n – есть относительная частота W1 значения х1, m2/n – относительная частота W2 значения х2 и т. д., запишем соотношение так:
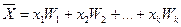 (*)
(*)
Допустим, что число испытаний достаточно велико. Тогда относительная частота приближенно равна вероятности появления события (доказательство опустим):
W1 ≈ p1, W2 ≈ p2,..., Wk ≈ pk.
Заменив в соотношении (*) относительные частоты соответствующими вероятностями, получим

Правая часть этого приближенного равенства есть М(X). Итак,

Вероятностный смысл полученного результата таков: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Замечание 1. Легко сообразить, что математическое ожидание больше наименьшего и меньше наибольшего возможных значений. Другими словами, на числовой оси возможные значения расположены слева и справа от математического ожидания. В этом смысле математическое ожидание характеризует расположение распределения и поэтому его часто называют центрам распределения.
Замечание 2. Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI–XVII вв.), когда область ее применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша, или, иными словами, математическое ожидание выигрыша.