Определение случайной величины

Интуитивное представление о случайной величине

Случайная величина – это числовая функция, значения которой заранее (до наблюдения) нельзя точно определить, то есть функция, зависящая от случайного исхода и принимающая свои значения с некоторыми вероятностями.

Примеры случайных величин:

а) число пассажиров в автобусе (конечное число значений);

б) число вызовов на телефонной станции за время Т (счетное число значений);

в) время безотказной работы прибора за время Т (несчетное число значений).

Обозначают случайные величины прописными буквами латинского алфавита X, Y, Z, …, а их значения соответствующими строчными буквами x, y, z, ….

Определение случайной величины

Пусть задано некоторое вероятностное пространство .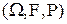

Определение. Функция 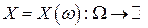называется случайной величиной, если для любого 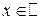множество

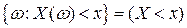
является событием, то есть .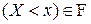

Смысл приведенного определения случайной величины состоит в требовании того, чтобы у подмножества 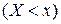была определена его вероятность при любом .

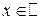Определение. Говорят, что функция 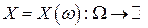является
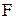-измеримой, если множество для любого .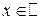

Таким образом, случайная величина есть 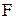-измеримая функция, ставящая в соответствие каждому элементарному исходу 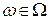число .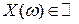

Из определения случайной величины и свойств -алгебры вытекает, что событиями являются также следующие подмножества, связанные со случайной величиной :

;

;

;

,

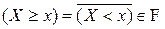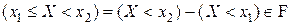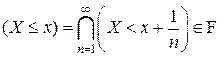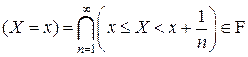и любые другие, получающиеся из них с помощью выполнения конечного или счетного числа операций. Другими словами, приведенное определение случайной величины эквивалентно тому, что попадание случайной величины в любое борелевское множество на числовой прямой является событием: для любого .

Заметим, что, если в -алгебре 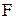содержатся все подмножества 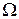(как, например, в случае конечного или счетного 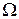), то случайной величиной является любая числовая функция 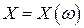. В общем случае это не так.