Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства математического ожидания. Во всех рассматриваемых ниже свойствах предполагается, что у случайных величин математические ожидания существуют.
|
|
Во всех рассматриваемых ниже свойствах предполагается, что у случайных величин математические ожидания существуют.
М0). Математическое ожидание любой случайной величины есть число!
М1). Математическое ожидание постоянной 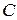 равно этой постоянной:
равно этой постоянной:
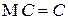 .
.
М2). Постоянная величина выносится за знак математического ожидания:
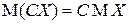 .
.
М3). Математическое ожидание суммы любых случайных величин  и
и 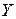 равно сумме их математических ожиданий:
равно сумме их математических ожиданий:
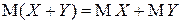 .
.
Замечание. Свойства М1), М2) и М3) называются свойствами линейности математического ожидания и следуют из свойств линейности рядов и интегралов в соответствии с формулами (2.7) и (2.8).
Следующие два свойства математического ожидания связаны с понятием
«Р-почти наверное» (Р-п.н.). Говорят, что некоторое свойство выполнено Р-п.н., если существует множество 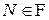 с
с 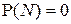 такое, что это свойство выполнено для каждого
такое, что это свойство выполнено для каждого 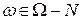 . Вместо Р-п.н. говорят также «Р-почти всюду» (Р-п.в.) или просто «почти наверное» (п.н.), «почти всюду» (п.в.). Используют также термин: свойство выполнено с вероятностью 1.
. Вместо Р-п.н. говорят также «Р-почти всюду» (Р-п.в.) или просто «почти наверное» (п.н.), «почти всюду» (п.в.). Используют также термин: свойство выполнено с вероятностью 1.
М4). Если 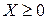 п.н. (то есть
п.н. (то есть 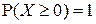 ), то
), то 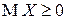 .
.
Если 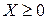 п.н. и при этом
п.н. и при этом 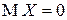 , то
, то 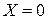 п.н. (то есть
п.н. (то есть 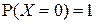 ).
).
▲ Доказательство свойства для дискретных случайных величин очевидно. Для непрерывных случайных величин доказательство следует из того, что плотность вероятностей  при
при 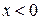 ■.
■.
М5). Если  п.н., то
п.н., то 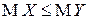 .
.
Если  п.н. и при этом
п.н. и при этом 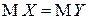 , то
, то 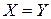 п.н..
п.н..
▲ Для доказательства достаточно применить свойство М4) к случайной величине 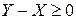 п.н. ■.
п.н. ■.
М6). 
▲ Поскольку 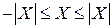 для любого
для любого 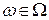 , то в силу свойства М5)
, то в силу свойства М5) 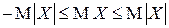 , то есть
, то есть  ■.
■.
Замечание. Свойство М6) справедливо и в более общем виде:
Для любой выпуклой вниз функции 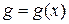 справедливо неравенство:
справедливо неравенство:
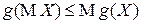 (неравенство Йенсена).
(неравенство Йенсена).
Моменты. Дисперсия. Среднее квадратическое отклонение.
Кроме математического ожидания, в теории вероятностей используется еще ряд числовых характеристик различного назначения. Среди них основную роль играют моменты – начальные и центральные.
Определение. Начальным моментом 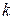 -го порядка случайной величины
-го порядка случайной величины  называется математическое ожидание
называется математическое ожидание 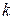 -ой степени этой случайной величины:
-ой степени этой случайной величины:
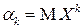 , (2.9)
, (2.9)
если математическое ожидание существует.
Как правило, используют начальные моменты  целого положительного порядка. В частности, при
целого положительного порядка. В частности, при 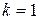 имеем
имеем 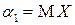 , а при
, а при 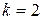
 .
.
Определение. Центральным моментом 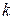 -го порядка случайной величины
-го порядка случайной величины  называется математическое ожидание
называется математическое ожидание 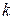 -ой степени отклонения этой случайной величины от ее математического ожидания:
-ой степени отклонения этой случайной величины от ее математического ожидания:
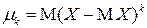 , (2.10)
, (2.10)
если математическое ожидание существует.
Случайная величина 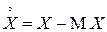 называется центрированной случайной величиной. Очевидно,
называется центрированной случайной величиной. Очевидно, 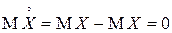 . Таким образом, центральный момент – это начальный момент для центрированной случайной величины:
. Таким образом, центральный момент – это начальный момент для центрированной случайной величины:
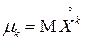 .
.
Аналогично начальным моментам, используются центральные моменты 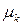 , как правило, целого положительного порядка. В частности, при
, как правило, целого положительного порядка. В частности, при 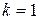 имеем
имеем 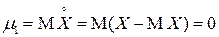 для всех случайных величин.
для всех случайных величин.
Особое значение для практики имеет второй центральный момент 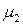 , который называется дисперсией случайной величины и обозначается
, который называется дисперсией случайной величины и обозначается  .
.
Определение. Дисперсией случайной величины  называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
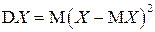 . (2.11)
. (2.11)
Для дисперсии 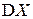 справедливо также следующее выражение:
справедливо также следующее выражение:
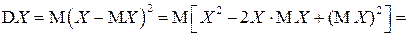
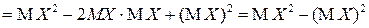
Таким образом, наряду с (2.11), имеем эквивалентное определение дисперсии 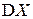 :
:
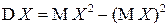 . (2.12)
. (2.12)
С помощью формулы (2.12) на практике вычислять дисперсию часто бывает проще.
Дисперсия  характеризует степень разброса (рассеивания) значений случайной величины относительно ее среднего значения (математического ожидания). Чем плотнее группируются значения случайной величины около математического ожидания, тем дисперсия меньше (ср. со смыслом параметра
характеризует степень разброса (рассеивания) значений случайной величины относительно ее среднего значения (математического ожидания). Чем плотнее группируются значения случайной величины около математического ожидания, тем дисперсия меньше (ср. со смыслом параметра 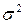 в нормальном законе распределения).
в нормальном законе распределения).
Механическая интерпретация дисперсии. Дисперсия представляет собой момент инерции распределения масс относительно центра масс (центра тяжести, математического ожидания).
Вычисляются начальные моменты  по формулам, вытекающим из основной теоремы о математическом ожидании для функции
по формулам, вытекающим из основной теоремы о математическом ожидании для функции 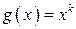 :
:
если Х – дискретная случайная величина, то
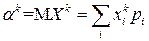 ;
;
если Х – непрерывная случайная величина, то
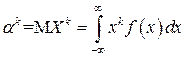 .
.
Центральные моменты 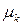 вычисляются по формулам, вытекающим из основной теоремы о математическом ожидании для функции
вычисляются по формулам, вытекающим из основной теоремы о математическом ожидании для функции 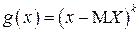 :
:
если Х – дискретная случайная величина, то
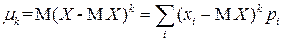 ;
;
если Х – непрерывная случайная величина, то
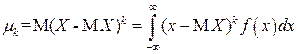 .
.
Формулы для вычисления дисперсии 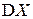 вытекают из основной теоремы о математическом ожидании для функции
вытекают из основной теоремы о математическом ожидании для функции 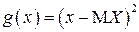 , если используется формула (2.11), или для функции
, если используется формула (2.11), или для функции 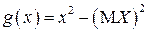 , если используется формула (2.12):
, если используется формула (2.12):
если Х – дискретная случайная величина, то

если Х – непрерывная случайная величина, то