
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача № 10.
|
|
10.1. По некоторой цели производятся два выстрела. Вероятность попадания при одном выстреле равна P. Рассматриваются две случайные величины: Х - число попаданий в цель, Y - число промахов. Составить таблицу распределения и определить числовые характеристики системы.



 10.2. Случайная точка на плоскости распределена по закону, заданному таблицей:
10.2. Случайная точка на плоскости распределена по закону, заданному таблицей:
 Y X 0 1
Y X 0 1
 -1 0, 1 0, 15
-1 0, 1 0, 15
 0 0, 15 0, 25
0 0, 15 0, 25
1 0, 2 0, 15
Найти числовые характеристики системы (X, Y).
 10.3. Матрица распределения системы двух дискретных случайных величин(X, Y) задана таблицей: X Y 0 2 5
10.3. Матрица распределения системы двух дискретных случайных величин(X, Y) задана таблицей: X Y 0 2 5
1 0, 1 0 0, 2
2 0 0, 3 0
4 0, 1 0, 3 0
Найти числовые характеристики системы (Х, Y).
10.4. Изготовляемые в цехе втулки сортируются по отклонению их внутреннего диаметра от номинального размера на 4 группы со значениями 0, 01; 0, 02; 0, 03 и 0, 04 мм и по овальности на четыре группы 0, 002; 0, 004; 0, 006;
 0, 008 мм. Совместное распределение диаметра (X) и овальности (Y) втулок задано таблицей (Табл.10.3):
0, 008 мм. Совместное распределение диаметра (X) и овальности (Y) втулок задано таблицей (Табл.10.3):
Y Х 0, 01 0, 02 0, 03 0, 04
0, 002 0, 01 0, 02 0, 03 0, 04
0, 004 0, 03 0, 24 0, 15 0, 06
0, 004 0, 04 0, 10 0, 08 0, 08
0, 008 0, 02 0, 04 0, 04 0, 02
Найти числовые характеристики системы случайных величин  .
.
10.5. Дана таблица, определяющая закон распределения системы двух cлучайных величин (X, Y):




 Y
Y
X 20 40 60
 10 3
10 3 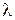
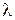 0
0

 20 2
20 2 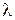 4
4 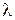 2
2 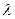
30 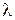 2
2 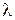 5
5 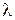
Найти: 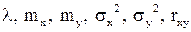 .
.
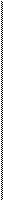




 10.6. Система (X, Y) задана следующей двумерной таблицей распределения вероятностей:
10.6. Система (X, Y) задана следующей двумерной таблицей распределения вероятностей:
X 0 1 2 3 4 5 6
 Y
Y
 0 0, 202 0, 174 0, 113 0, 062 0, 049 0, 023 0, 004
0 0, 202 0, 174 0, 113 0, 062 0, 049 0, 023 0, 004
 1 0 0, 099 0, 064 0, 040 0, 031 0, 020 0, 006
1 0 0, 099 0, 064 0, 040 0, 031 0, 020 0, 006
 2 0 0 0, 031 0, 025 0, 018 0, 013 0, 008
2 0 0 0, 031 0, 025 0, 018 0, 013 0, 008
3 0 0 0 0, 001 0, 002 0, 004 0, 011
Найти вероятность 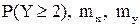 и корреляционную матрицу.
и корреляционную матрицу.
10.7. Однотипные детали в зависимости от точности изготовления различаются по форме на круглые и овальные, а по весу - на легкие и тяжелые. Вероятности того, что взятая наудачу деталь окажется круглой и легкой, овальной и легкой, круглой и тяжелой, овальной и тяжелой, соответственно равны 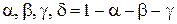 . Взята одна деталь. Найти математические ожидания и дисперсии числа круглых деталей X и числа легких деталей Y, а также корреляционный момент kxy между числом круглых и числом легких деталей, если
. Взята одна деталь. Найти математические ожидания и дисперсии числа круглых деталей X и числа легких деталей Y, а также корреляционный момент kxy между числом круглых и числом легких деталей, если  = 0, 40,
= 0, 40, 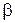 = 0, 05,
= 0, 05, 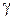 = 0, 10.
= 0, 10.
10.8. Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна P. Случайные величины: X - число выстрелов до первого попадания (включительно), Y - число промахов. Необходимо: а) описать закон распределения случайного вектора (X, Y) и законы распределения каждой компоненты; б) вычислить вероятность P(X = Y);
в) вычислить коэффициент корреляции rxy.; г) определить зависимы или неза-висимы компоненты X, Y.
10.9. Бросаются две одинаковые игральные кости. Случайные величины:
X - индикатор четности суммы выпавших очков (т.е. X = 1, если эта сумма четная, и X = 0 в противном случае), Y - индикатор четности произведения выпавших очков (т.е. Y = 1, если это произведение четно и Y = 0 в противном случае).
а) Описать закон распределения случайного вектора (X, Y).
б) Вычислить функцию распределения F(X, Y).
в) Вычислить корреляционный момент.
10.10. Число X выбирается случайным образом из множества целых чисел
 . Затем из того же множества выбирается наудачу число Y, больше первого или равное ему.
. Затем из того же множества выбирается наудачу число Y, больше первого или равное ему.
а) Описать закон распределения случайного вектора (X, Y).
б) Определить, зависимы или независимы случайные компоненты X и Y.
в) Построить условный закон распределения компоненты X при условии, что Y приняло значение, равное 2.
г) Вычислить основные характеристики 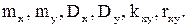
10.11. Случайный вектор (X, Y) имеет следующее распределение вероятностей:



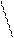
 Y X 0 1
Y X 0 1
 -1 0, 1 0, 2
-1 0, 1 0, 2
 0 0, 2 0, 2
0 0, 2 0, 2
1 0, 1 0, 2
Найти математическое ожидание и дисперсию величины 
10.12. В продукции завода брак вследствие дефекта A составляет 3 %, а вследствие дефекта B - 4, 5 %. Годная продукция составляет 95 %. Найти коэффициент корреляции дефектов A и B. Указание. Ввести в рассмотрение случайную величину X = 1, если данное изделие обладает дефектом A и X = 0 в противном случае. Аналогично Y = 1; 0 в зависимости от того, обладает или нет это изделие дефектом B.
10.13. Два стрелка, независимо друг от друга, делают по два одиночных (независимых) выстрела каждый по своей мишени. Случайная величина X - число попаданий первого стрелка, Y - число попаданий второго стрелка. Вероятность попадания при одном выстреле для первого стрелка P1 = 0, 7; для второго P2 = 0, 4. Построить матрицу распределения вероятностей системы случайных величин (X, Y).
10.14. Два стрелка независимо друг от друга делают по одному выстрелу каждый по своей мишени. Случайная величина X - число попаданий первого стрелка. Y - число попаданий второго стрелка. Вероятность попадания при одном выстреле для первого стрелка P1 = 0, 7, для второго P2 = 0, 4. Построить матрицу распределения вероятностей системы случайных величин (u, v), где 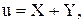
 .
.

 10.15. Система случайных величин (Х, Y) имеет следующее распределение вероятностей:
10.15. Система случайных величин (Х, Y) имеет следующее распределение вероятностей:
 Y X 0 1
Y X 0 1
-1 0, 1 0, 2

 0 0, 2 0, 3
0 0, 2 0, 3
1 0 0, 2
Найти математическое ожидание и дисперсию случайной величины 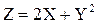 .
.
10.16. Имеется система случайных величин (X, Y), где
 и коэффициент корреляции
и коэффициент корреляции 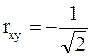 . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины 
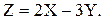
10.17. Случайные величины X и Y связаны соотношением 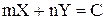 , где
, где 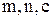 - неслучайные величины
- неслучайные величины  . Найти: а) Коэффициент корре-ляции
. Найти: а) Коэффициент корре-ляции 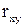 ; б) Отношение среднеквадратических отклонений
; б) Отношение среднеквадратических отклонений 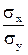 .
.
10.18. Дважды бросается игральная кость. Случайные величины: X - число появлений шестерки, Y - число появлений нечетной цифры. Описать закон распре-деления случайного вектора (X, Y). Установить зависимы или независимы компоненты Х и Y.
10.19.Дважды бросается игральная кость. Случайные величины: X - число появлений единицы, Y - число появлений нечетной цифры. Описать закон распре-деления случайного вектора (X, Y). Вычислить основные характеристики случайного вектора: 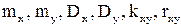 .
.
10.20. Дважды бросается игральная кость. Случайные величины: X - число появлений шестерки, Y - число появлений четной цифры. Описать закон распределения случайного вектора (X, Y). Описать условный закон распределения случайной величины X при условии Y = 2 и при этом условии вычислить условное математическое ожидание 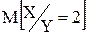 .
.
10.21. Совместное распределение (X, Y) задано формулами:
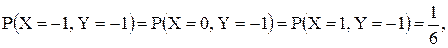
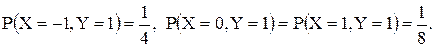
Найти одномерные распределения X, Y и распределения 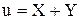 .
.
10.22. Совместное распределение  задано формулами:
задано формулами:

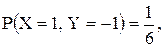
 ,
,
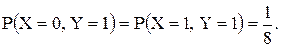
Найти совместное распределение случайных величин: 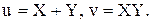
10.23. Совместное распределение (X, Y) задано формулами
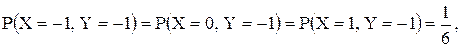

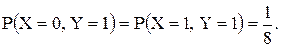
Найти 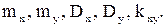
10.24. Совместное распределение случайных величин определяется формулами

Найти 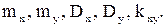 Являются ли X, Yнезависимыми величинами?
Являются ли X, Yнезависимыми величинами?
10.25. Случайные величины 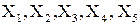 независимы;
независимы; 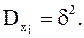 Найти:
Найти:
а) коэффициент корреляции величин Х1+Х2, Х3+Х4+Х5; б) коэффициент корреляции величин Х1+Х2+Х3, X3+X4+X5 .
10.26.Дана таблица, определяющая закон распределения системы двух случайных величин (Х, Y):

X Y 2 4 6
1 l 3 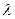 0
0
2 4 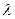 2
2 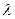 2
2 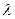
3 5 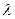 2
2 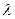 l
l
Найти: а). 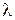 , б).
, б). 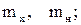 в).
в). 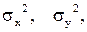 г)
г) 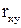 .
.

 10.27. Система случайных величин (Х, Y)распределена по закону, выраженному таблицей:
10.27. Система случайных величин (Х, Y)распределена по закону, выраженному таблицей:
 Y X 0 1
Y X 0 1
 -1 0, 1 0, 15
-1 0, 1 0, 15
 0 0, 15 0, 25
0 0, 15 0, 25
1 0, 2 0, 15
Описать условный закон распределения случайной величины Х, при условии Y = 0, при этом же условии вычислить условное математическое ожидание 

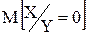 .
.
 10.28. В таблице приведены данные о возможных сочетаниях отклонений длины валика (Х) и диаметра (Y) от номинальных размеров и соответствующие вероятности:
10.28. В таблице приведены данные о возможных сочетаниях отклонений длины валика (Х) и диаметра (Y) от номинальных размеров и соответствующие вероятности:
| X Y | -1 | ||
| -2 | 0, 15 | 0, 35 | 0, 05 |
| 0, 10 | 0, 25 | 0, 10 |
Найти закон распределения случайной величины Z = X + Y и проверить справед-ливость формулы 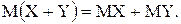








 10.29. Случайные величины
10.29. Случайные величины  независимы. По заданным законам распреде-ления случайных величин
независимы. По заданным законам распреде-ления случайных величин  найти закон распределения системы случайных величин
найти закон распределения системы случайных величин 

 X 1 2 3 Y 4 6 8 10
X 1 2 3 Y 4 6 8 10
P 0, 3 0, 5 0, 2 P 0, 1 0, 4 0, 3 0, 2
10.30. Дважды бросается игральная кость. Случайные величины: Х - число появлений шестерки, Y - число появлений нечетной цифры. Вычислить вероятности  .
.