Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача № 11.
|
|
11.1. Система случайных величин имеет равномерное распределение внутри квадрата со стороной a. Диагонали квадрата совпадают с осями координат. Определить: а) плотность совместного распределения вероятностей системы (X, Y);
б) плотность распределения вероятностей каждой из случайных величин, входящих в систему.
11.2. Система трех случайных величин (X, Y, Z) распределена равномерно внутри цилиндра, ось которого совпадает с осью OZ и точкой O делится пополам. Радиус цилиндра равен R, а высота 2h. Определить: а) плотность совместного распределения вероятностей системы (X, Y, Z); б) плотность распределения каждой из случайных величин, входящих в систему.
11.3. Система случайных величин (X, Y) подчинена закону распределения с плотностью распределения вероятностей 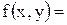
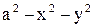 , если
, если 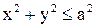 и
и  если
если 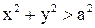 . Найти: 1) a; 2)
. Найти: 1) a; 2) 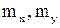 ; 3)дисперсии
; 3)дисперсии 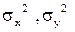 ;
;
4) коэффициент корреляции 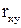 .
.
11.4. Система двух случайных величин (X, Y) подчинена нормальному закону распределения. Рассеивание круговое. Найти вероятность попадания случайной точки (X, Y) в круг, центр которого cовпадает с центром рассеивания, а радиус равен двум вероятным отклонениям (Вероятное отклонение 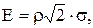 где
где
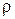 = 0, 476936).
= 0, 476936).
11.5. Плотность совместного распределения вероятностей системы случайных величин X, Y имеет вид: 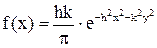 , где
, где 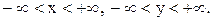 Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.
Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.
11.6. Плотность совместного распределения системы случайных величин X, Y:
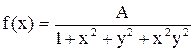 . Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
. Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
11.7. Система двух случайных величин (X, Y) подчинена закону распределения с плотностью совместного распределения:  . Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.
. Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.
11.8. Система случайных величин (X, Y) имеет плотность совместного распределения
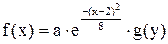 , где
, где 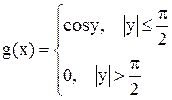 . Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.
. Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.
11.9. Производится единичное бомбометание по прямоугольной наземной цели. Ширина цели равна 20 м, а длина 100 м. Прицеливание по центру цели. Оси рассеивания совпадают с направлением полета и с перпендикуляром к этому направлению. Вероятное отклонение в направлении полета равно 60 м, в направлении, перпендикулярном полету – 40 м. Систематические ошибки отсут-ствуют. Вероятность попадания в цель при сбрасывании одной бомбы. Указание: Вероятное отклонение 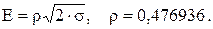
11.10. Плотность совместного распределения системы случайных величин X, Y равна  . Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.
. Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.
11.11. Дана плотность совместного распределения случайных величин X, Y:
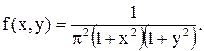 Определить вероятность попадания в прямоугольник:
Определить вероятность попадания в прямоугольник:
 y
y
 (2; 1, 5)
(2; 1, 5)
 (0; -1) (2; -1) х
(0; -1) (2; -1) х
11.12. Система случайных величин (X, Y) распределена с постоянной плот-ностью внутри квадрата. Найти плотности распределения случайных величин X, Y входящих в систему:
Y
 1
1
-1 1 x
-1
11.13. Система случайных величин (X, Y) подчинена закону распределения с плотностью:
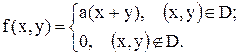
Область D - квадрат, ограниченный линиями x = 0; x = 3; y = 0; y = 3.
Найти: а) Коэффициент a; б) вероятность попадания случайной точки (x, y) в квадрат, ограниченный прямыми x = 1, x = 2, y = 1, y = 2; в) 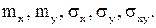
11.14. Определить плотность распределения вероятностей, математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если 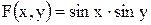 ,
, 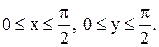
11.15. Плотность совместного распределения случайных величин (X, Y): 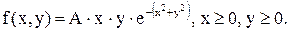 Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
кие ожидания каждой из случайных величин.
11.16. Плотность совместного распределения системы случайных величин X, Y равна 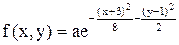 . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
. Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
11.17. Координаты случайной точки (X, Y) раcпределены равномерно внутри прямоугольника, ограниченного прямыми x = 0, x = a, y = 0, y = b. Определить вероятность попадания случайной точки в круг радиуса R = a, если a > b, а центр круга совпадает с началом координат.
11.18. Координаты (X, Y) случайной точки распределены равномерно внутри прямоугольника, ограниченного прямыми x = a, x = b, y = c, y = d (в > a, d > c). Найти плотность распределения вероятностей и функцию распределения системы случайных величин X, Y. Выяснить, являются ли X, Yнезависимыми величинами.
11.19. Плотность совместного распределения случайных величин X, Y равна:
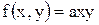 в области D и f(x, y)=0 вне этой области. Область D- треугольник, ограниченный прямыми
в области D и f(x, y)=0 вне этой области. Область D- треугольник, ограниченный прямыми  Найти а)
Найти а) 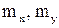 ; б) коэффициент корреляции
; б) коэффициент корреляции 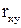 , дисперсии
, дисперсии 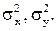
11.20. Плотность совместного распределения системы случайные величины
(X, Y), заданной внутри круга радиуса R, равна 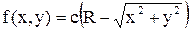 . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
. Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
11.21. Плотность совместного распределения системы случайных величин
(X, Y): 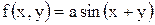 в области D и
в области D и 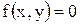 вне этой области. Область D определяется неравенствами
вне этой области. Область D определяется неравенствами  Определить: a) постоянную a;
Определить: a) постоянную a;
б) 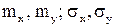 ; в) определить коэффициент корреляции r xy.
; в) определить коэффициент корреляции r xy.
11.22. Дана плотность совместного распределения системы случайных величин 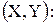
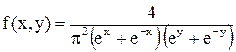 . Определить вероятность попадания случайной точки (x, y)в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
. Определить вероятность попадания случайной точки (x, y)в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
11.23. Плотность распределения вероятностей двумерного случайного вектора (X, Y)имеет следующий вид: 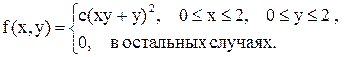 .
.
Вычислить: а) значение постоянной c; б) вероятность 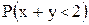 ); в) центр рассеивания.
); в) центр рассеивания.
11.24. Случайные величины X и Y независимы и распределены каждая по показательному закону с параметрами соответственно l1 и l2. Найти вероятность 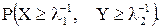
11.25. Функция совместного распределения двух случайных величин X и Y имеет следующий вид:
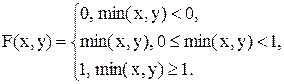
Найти одномерные законы распределения компонент и решить вопрос об их зависимости или независимости.
11.26. Случайные величины X и Y независимы и распределены следующим образом: X - по закону N(1; 2), Y - по равномерному закону на отрезке [0; 2].
Найти вероятность следующих событий: 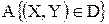 , где область
, где область
D = {(x, y) / (0 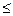 x
x 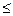 2, 0
2, 0 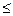 y
y 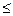 1); B = {X > Y}.
1); B = {X > Y}.
11.27. Случайная точка на плотности (X, Y) распределена по круговому нормальному закону (rxy = 0, sx = sy = s = 1,) с центром рассеивания в начале координат. Вычислить вероятности следующих событий: A = {Y > X},
B = {ç Yç > X}, C = {Y < 3X}, D = {ç Xç < 1}, E = {X < 1, Y < 2}.
11.28. Заданы следующие характеристики двумерного нормального вектора:
mx = -2; my = 3 и ковариационная матрица 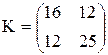 . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2sx, b = 2sy.
. Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2sx, b = 2sy.
11.29. Определить вероятность попадания точки с координатами (X, Y) в область, определяемую неравенствами (1 £ X £ 2, 1 £ Y £ 2), если функция распреде-ления 
11.30. Определить математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если плотность распределения вероятностей