
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы получения равномерно распределенных случайных чисел.
|
|
При моделировании процессов и сист.исп-ся 3 вида случ.объектов. 1.сл.величины, 2.сл.события, 3.сл.процессы. Сл.величина-сл.время, сл.события-работоспос.сист. в сл.момент времени сл.события. Всегда необходима выработка случ.чисел. 1.кол-во выр-х чисел должно быть достаточно большим. Возможность создания им.модели оч.сильно зависит от наличия экон и простых способов получения чисел.
Получение случ.чисел [0, 1]; (0, 1); (0, 1]. Способы получения. Пусть ξ € (0, 1]-равном.распр.случ.величина. x€(a, b]-любой интервал. X=a+(b-a)ξ -перераспред.
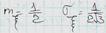 если мы хотим получить равном.распр.число, то надо взять число
если мы хотим получить равном.распр.число, то надо взять число 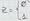 с вероятностью ½. Создадим случ.послед-ть zi, z1, z2, …считая ее бесконечной, тогда величина, постр. В виде
с вероятностью ½. Создадим случ.послед-ть zi, z1, z2, …считая ее бесконечной, тогда величина, постр. В виде  , будет случайным числом. Вероятность попадания сл.величины в интервал длиной ½ равна длине интервала. Раз вероятность попадания равна ½ то что нужно сгенерировать бескон.послед.сл.величин z1…zn и считать их двоичными знаками ξ. Проблема, если zi→ ∞, то число тоже бесконечное, но на машине это сделать нельзя, можно ген-ть определенную конечную послед-ть. Если если комп.с k разр.сеткой, то в ней можно записать k разл.чисел с одинак.вер-ми
, будет случайным числом. Вероятность попадания сл.величины в интервал длиной ½ равна длине интервала. Раз вероятность попадания равна ½ то что нужно сгенерировать бескон.послед.сл.величин z1…zn и считать их двоичными знаками ξ. Проблема, если zi→ ∞, то число тоже бесконечное, но на машине это сделать нельзя, можно ген-ть определенную конечную послед-ть. Если если комп.с k разр.сеткой, то в ней можно записать k разл.чисел с одинак.вер-ми 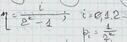 .
.