Дискретні випадкові величини

Законом розподілу дискретної випадкової величини називається відповідність між можливими значеннями випадкової величини (або множинами значень) та ймовірностями, що їм відповідають.

Його можна задати у вигляді таблиці, формули або графіка.

			........	........
			........	........

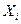
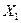
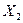
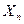
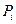
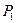
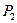
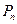
Події, яким відповідають числові значення випадкової величини X: 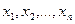, утворюють повну групу, тому .

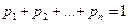Біноміальний закон розподілу є такий закон розподілу дискретної випадкової величини Х – числа появи подій в незалежних випробуваннях за схемою Бернуллі, в кожному з яких ймовірність настання події дорівнює p. Ймовірність можливого значення Х=k- числа появи події обчислюється за формулою Бернуллі

.

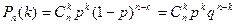Закон Пуассона Якщо число випробувань велике, а ймовірність р настання події в кожному випробуванні незначна, то використовують наближену формулу

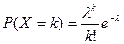
, де k- число появи події в незалежних випробуваннях.

Математичним сподіванням дискретної випадкової величини називають суму добутків всіх її можливих значень на їх ймовірності:

.

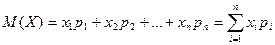Математичне сподівання біноміального розподілу дорівнює добутку числа випробувань n на ймовірність p появи події в одному випробуванні:

.

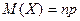Для розподілу Пуассона .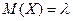

Математичне сподівання дискретної випадкової величини є величина невипадкова (стала).

На числовій осі можливі значення випадкової величини X розміщені зліва та справа від математичного сподівання. Тому його часто називають центром розподілу.

Дисперсією (розсіюванням) дискретної випадкової величини називається математичне сподівання квадрата відхилення дискретної випадкової величини від математичного сподівання:

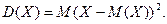
При обчисленні дисперсії доцільно використовувати формулу:

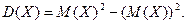
Величина

,

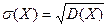називається середнім квадратичним відхиленням випадкової величини Х. Дисперсія біноміального розподілу дорівнює добутку числа випробувань на ймовірність появи і не появи події в одному випробуванні

.

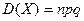Для розподілу Пуассона .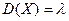

Приклад 1. В грошовій лотереї випущено 100 білетів. Розігрується один виграш у 50 гривень і 10 виграшів по 1 гривні. Знайти закон розподілу, математичне сподівання, дисперсію і середнє квадратичне відхилення дискретної випадкової величини Х- вартості можливого виграшу для власника одного лотерейного білету.

Розв’язування: Випишемо можливі значення виграшу Х:

х₁=0 (нічого не виграв);

х₂=1(виграв 1 грн.);

х₃=50 (виграв 50 грн.).

Ймовірності цих можливих значень дорівнюють:

.

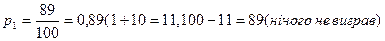
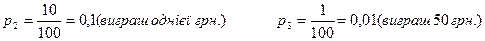Тоді закон розподілу має вигляд:

Перевіримо контрольну суму: 0, 89+0, 1+0, 01=1.

Знайдемо математичне сподівання:

М(х)=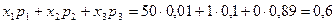

Порахуємо дисперсію D(X), для цього попереднє побудуємо закон розподілу для Х²:

І знайдемо її математичне сподіванням

,

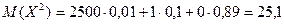тоді .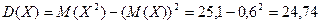

Середнє квадратичне відхилення: .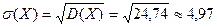

Приклад 2. Випадкова величина Х задана законом розподілу

Знайти: середнє квадратичне відхилення дискретної випадкової величини Х.

Розв’язування: 1)Знайдемо математичне сподівання: ;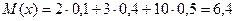

2)Знайдемо математичне сподівання для Х²: ;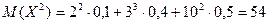

3) Порахуємо дисперсію ;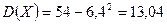

4) Середнє квадратичне відхилення: .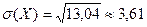

Приклад 3. Насіння проростає з імовірністю 0, 8. Розглядають випадкову величину X – кількість зерен, які проросли серед п’яти посіяних. Знайти закон розподілу дискретної випадкової величини X у вигляді ряду розподілу.

Розв’язування:

▼ Враховуючи, що випадкова величина X може набувати одного з можливих числових значень 0, 1, 2, 3, 4, 5, (проростання зерен) то вектор значень має вигляд:

,

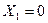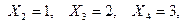
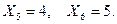
Ймовірності Р_і шукатимемо за формулою Бернуллі 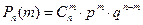, причому, за умовою маємо такі значення параметрів: p = 0.8, q = 0.2, n = 5. Підставимо замість m відповідні значення випадкової величини. Підставою застосування формули Бернуллі є незалежність випробувань і закони розподілів ймовірностей в окремих випробуваннях співпадають. З урахуванням цього вектор ймовірностей має вигляд:

Р1=Р5(0)= .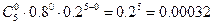

; ; ; .

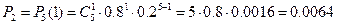
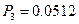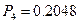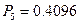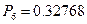Тоді отримаємо такий ряд розподілу:

Приклад 4. Ймовірності того, що студент складе семестровий іспит з дисциплін А та В під час сесії, становлять відповідно 0, 7 та 0, 9. Скласти закон розподілу числа семестрових іспитів, які студент складе в сесію у вигляді ряду розподілу.

Розв’язування:

Можливі значення випадкової величини X - числа семестрових іспитів, які студент складе в сесію – 09 не здасть іспит), 1(здасть один), 2(здасть два).

Нехай А_і - незалежні події, які полягають у тому, що студент складе і - й іспит. Тоді ймовірності того, що студент складе в сесію 0, 1, 2 іспити, будуть відповідно рівні:

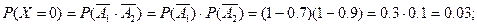
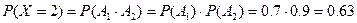
Отже, ряд розподілу випадкової величини X має вигляд:

.

Приклад 5. Побудувати очікуваний розподіл результатів іспитів для 256 студентів, які абсолютно нічого не знають з дисципліни і випадково вгадують відповіді на чотири питання з чотирма можливими варіантами відповідей на кожне з них (тільки одна з чотирьох відповідей правильна).

Розв’язування:

Вгадування кожним студентом відповідей на чотири питання можна інтерпретувати як n = 4 випробувань Бернуллі. При цьому, оскільки студенти нічого не знають, то для них рівноймовірні всі чотири відповіді на кожне питання, тобто ймовірність успіху (правильної відповіді на питання) рівна р =1/4. Тоді число Х вгаданих одним студентом відповідей на чотири питання являє собою біноміальну випадкову величину Х 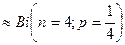і х=0, 1, 2, 3, 4,

Р_n(x)=БИНОМРАСП(х; n; р; 1)

БИНОМРАСП (число успехов; число испытаний; вероятность успеха; интегральная)

Р₄(0)= БИНОМРАСП(0; 4; 0, 25; 0)=0, 31641

Р₄(1)= БИНОМРАСП(1; 4; 0, 25; 0)=0, 421875

Р₄(2)= БИНОМРАСП(2; 4; 0, 25; 0)=0, 2109375

Р₄(3)= БИНОМРАСП(3; 4; 0, 25; 0)=0, 046875

Р₄(4)= БИНОМРАСП(4; 4; 0, 25; 0)=0, 00390625

а очікуваний розподіл результатів іспитів для 256 студентів, враховуючи їх незалежність один від одного, буде мати наступний вигляд:

Число правильних відповідей, Хі
Число студентів, 256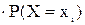

Математичне сподівання: .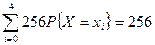

СРС

У деякій агенції кожне замовлення виконується частинами незалежно у трьох відділах. Ймовірність того, що якийсь відділ не виконає свою частину роботи вчасно, становити 0, 1. Скласти закон розподілу числа відділів, що не вклалися у термін виконання даного замовлення. Знайти ймовірність того, що більш ніж один відділ не вкладається у термін.