
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания и решения типовых задач
|
|
ГЛАВА 4 Средние величины
Средняя величина есть обобщенная количественная характеристика единиц совокупности по вариации определенного признака. Она рассчитывается на единицу этой совокупности. В статистике используются различные виды средних величин: агрегатная, арифметическая, гармоническая, геометрическая, средний квадрат и др. Выбор средней зависит как от поставленной задачи, которую правильно может разрешить только определенная средняя, так и от характера и содержания исходного материала, имеющегося в конкретном случае. При расчете средних величин необходимо исходить из экономического содержания статистических показателей.
В основе такого подхода лежит исходное соотношение средней, а именно:
| Средний уровень признака = | Итог значений признака по совокупности явлений |
| Число единиц совокупности |
Так, например, средняя урожайность представляет собой соотношение сбора урожая со всей площади (валовой сбор) и размера посевной площади (выраженной в гектарах). Уточняя исходное соотношение средней, можно сформулировать и более общее положение расчета средних величин (показателей): средние величины (показатели) рассчитываются таким же способом, как и индивидуальные показатели, только на основе данных по совокупности в целом. Если, например, уровень (процент) брака по отдельным предприятиям вычисляется делением объема бракованной продукции на объем всей продукции (результат деления умножается на 100), то по совокупности предприятий необходимо просуммировать объемы бракованной и всей продукции, а затем первое число разделить на второе, выражая полученный результат в процентах.
Уяснив экономическую природу средней величины, необходимо, чтобы все процедуры (операции) ее вычисления имели реальный смысл с точки зрения исходного соотношения средней.
Основанием для расчета средних величин является определяющее свойство средней, заключающееся в том, что сумма (произведение) индивидуальных значений признака равно сумме (произведению) средних значений признака по объему изучаемой совокупности. Это свойство свидетельствует о том, что средняя величина является уравнительным значением признака для всех единиц совокупности.
Реализуя исходное выражение расчета средней, используются различные формулы расчета средних величин.
Средняя арифметическая. Применяются формулы средней арифметической простой и взвешенной.
Если исходные данные осредняемого признака представлены в несгруппированном виде (как индивидуальные значения первичного признака у отдельных единиц совокупности), то в этом случае средняя рассчитывается по формуле средней арифметической простой:
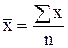 , (4.1)
, (4.1)
где 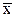 – среднее значение признака; х – индивидуальные значения признака у каждой единицы совокупности;
– среднее значение признака; х – индивидуальные значения признака у каждой единицы совокупности; 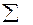 – знак суммирования; n – число единиц совокупности.
– знак суммирования; n – число единиц совокупности.
Если исходные данные представлены в сгруппированном виде, т.е. в виде рядов распределения (дискретных или интервальных), то средняя величина в таких случаях рассчитывается по формуле средней арифметической взвешенной:
 , (4.2)
, (4.2)
где х – варианты значений осредняемого признака; f – частоты (веса) для каждого из вариантов признака, показывающие их повторяемость.
Частоты ряда распределения можно заменить их удельными весами, т.е. частостями (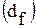 )
)
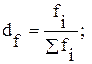 (4.3)
(4.3)
 (4.4)
(4.4)
В таких случаях формула расчета средней примет вид:
 , (4.5) или
, (4.5) или 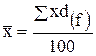 , (4.6) если удельные веса
, (4.6) если удельные веса 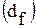 выражены в признаках.
выражены в признаках.
Средняя гармоническая. Если известны варианты значений осредняемого признака (х) и их суммарные (итоговые) результаты (M = xf), то в этом случае средняя рассчитывается по формуле средней гармонической взвешенной:
 . (4.7)
. (4.7)
Если вместо абсолютных значений (М), вычислить их удельные веса, т.е.
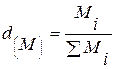 ; (4.8)
; (4.8)
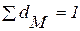 , (4.9)
, (4.9)
то формула расчета средней примет вид:
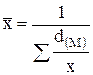 , (4.10)
, (4.10)
или 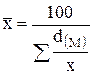 , (4.11)
, (4.11)
если удельные веса (dM) выражены в процентах
При M – const средняя гармоническая взвешенная преобразуется в среднюю гармоническую простую:
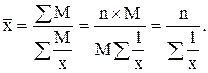 (4.12)
(4.12)
Задача 1. Имеются следующие условные данные об урожайности картофеля.
Таблица 4.1
| Хозяйства Номер п/п/ | Базисный период | Отчетный период | ||||
| Урожайность картофеля, ц/га (х) | Посевная площадь, га (f) | Доля посевной площади (df) | Урожайность картофеля, ц/га (х) | Валовой сбор картофеля, ц (М) | Посевная площадь картофеля, ц 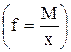
| |
| 0, 30 | ||||||
| 0, 20 | ||||||
| 0, 50 | ||||||
| Итого | 1, 0 |
Определим среднюю урожайность картофеля в базисном периоде, используя формулу средней арифметической взвешенной:
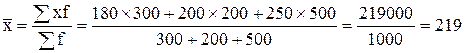 ц/га.
ц/га.
Такой же результат получим на основе данных доли посевов в общем их итоге (df):
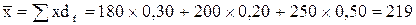 ц/га.
ц/га.
Вычислим среднюю урожайность картофеля в отчетном периоде, применив формулу средней гармонической взвешенной:
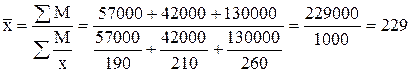 ц/га.
ц/га.
Во всех случаях, когда известны значения числителя и знаменателя исходного соотношения средней, средняя вычисляется по формуле средней агрегатной:
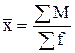 . (4.13)
. (4.13)
Применительно к отчетному периоду будем иметь среднюю урожайность картофеля:
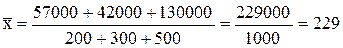 ц/га.
ц/га.
Средний квадрат. При решении ряда задач возникает необходимость вычисления среднего квадрата вариантов признака. Для этого случая используется формула: 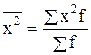 .
.
Задача 2. Имеются следующие условные данные штабелях бревен.
Таблица 4.2.
| №№ штабеля | ||||
| Радиус бревен в штабеле, см (r) | ||||
| Количество бревен, шт. (f) |
Известно, что 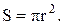 Среднюю площадь сечения бревна можно определить из выражения:
Среднюю площадь сечения бревна можно определить из выражения: 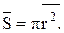
Для расчета среднего квадрата радиуса бревна используем формулу:
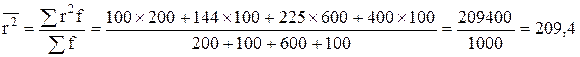 .
.
Величина средней площади сечения бревна составит: 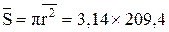 = =657, 516 см2.
= =657, 516 см2.
Расчет средних величин на основе взаимосвязи признаков. Например, затраты на производство валового сбора зерновых (3) можно представить произведением трех признаков: себестоимости 1 ц. зерна (z), урожайности зерновых (х) и размера посевной площади (f). Взаимосвязь указанных признаков посредством символов будет выражена:
З = zxf. (4.15)
Уровень средней урожайности зерновых культур определим на основе взаимосвязи признаков по следующей формуле:
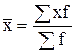 .
.
Средний уровень себестоимости 1 ц. зерновых культур будет вычислен по формуле:
 . (4.16)
. (4.16)
В каждом конкретном случае формула расчета среднего значения признака определяется экономическим содержанием взаимосвязи признаков и исходным соотношением расчета средней величины.
Вычисление средней арифметической по вариационным интервальным рядам. В подобных рядах необходимо предварительно по каждой группе от интервальных значений признака перейти к их дискретным выражениям путем определения полусумм нижней и верхней границ интервалов ряда распределения.
Средние затраты времени на одну деталь вычислим обычным (прямым) способом по формуле средней арифметической взвешенной (значения числителя и знаменателя формулы средней возьмем из табл. 4.3.):
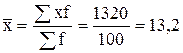 мин.
мин.
Задача 3. Имеются следующие данные о распределение деталей по затратам времени на их изготовление.
Таблица 5.3.
| Затраты времени на производство деталей, мин. | Количество деталей, шт. (f) | Середина интервала (х) | xf | x-A | 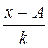
| 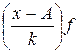
| Накопленные частоты |
| до 10 | -4 | -2 | -20 | ||||
| 10-12 | -2 | -1 | -10 | ||||
| 12-14 | |||||||
| 14-16 | |||||||
| 16 и выше | |||||||
| Итого |
В рядах распределения с равными интервалами значение средней вычислим по преобразованной формуле («способ условного момента»).
Вычислим среднюю арифметическую из значений 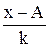 – первый условный момент (m1), где
– первый условный момент (m1), где 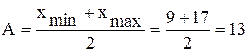 ; к – кратный делитель, равный величине интервала для рядов распределения с нечетным числом интервалов и
; к – кратный делитель, равный величине интервала для рядов распределения с нечетным числом интервалов и 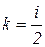 – для рядов распределения с четным числом интервалов (i – величина равного интервала).
– для рядов распределения с четным числом интервалов (i – величина равного интервала).
Первый условный момент исчисляется по формуле:
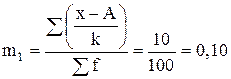 ;
;
а среднее значение признака
 мин.
мин.
Структурные средние. К их числу относятся мода, медиана и соответствующие квартильные характеристики. Мода (М0) – величина признака (варианта), которая встречается в ряду распределения с наибольшей частотой (весом). В дискретных рядах распределения значение моды определяется визуально, то есть по наибольшей частоте. Если же варианты ряда распределения заданы в виде интервалов, равных по величине, то сначала находится модальный интервал, т.е. интервал, обладающий наибольшей частотой, а затем – приближенное значение модальной величины признака по формуле:
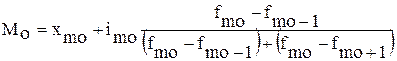 , (4.17)
, (4.17)
где xmo – нижняя граница модального интервала; imo – величина модального интервала; fmo-1 – частота интервала, предшествующего модальному; fmo – частота модального интервала; fmo+1 – частота интервала, следующего за модальным.
Вычислим значение модальной величины признака на основе данных табл. 4.3.:
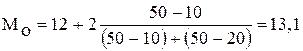 мин.
мин.
Медиана (Ме) – величина признака у единицы совокупности, находящейся в середине ранжированного (упорядоченного) ряда. Если ряд распределения представлен конкретными индивидуальными значениями признака в ранжированном порядке, то значение медианы находится как серединное значение признака (например, число значений нечетное – 55, то Ме соответствует 28-му в ряду значений признака; если же число значений четное – 56, то Ме соответствует полусумме 28 и 29 значений признака). Если варианты в ряду распределения представлены в виде равных интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для определения этого интервала сумму частот  делят пополам и на основе последовательного накопления (суммирования) частот интервалов, начиная с первого, находят интервал, где расположена медианная единица. Приближенное значение медианы в медианном интервале исчисляют по формуле:
делят пополам и на основе последовательного накопления (суммирования) частот интервалов, начиная с первого, находят интервал, где расположена медианная единица. Приближенное значение медианы в медианном интервале исчисляют по формуле:
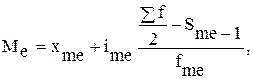 (4.18)
(4.18)
где хme – нижняя граница медианного интервала; ime – величина медианного интервала; 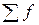 – сумма частот ряда; Sme-1 – накопленный итог численностей до медианного интервала; fme – численность медианного интервала.
– сумма частот ряда; Sme-1 – накопленный итог численностей до медианного интервала; fme – численность медианного интервала.
Вычислим значение медианной величины признака на основе данных табл. 4.3.:
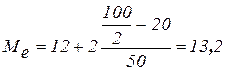 мин.
мин.
Следовательно, 50% изделий произведены с затратами времени 13, 2 мин и меньше на одну деталь, а 50% – больше, чем 13, 2 мин.
Квартили – это значения признака в ранжированном ряду, выбранные таким образом, что 25% единиц совокупности будут меньше величины Q1; 25% единиц будут заключены между Q1 и Q2; 25% – между Q2 и Q3; остальные 25% превосходят Q3. Квартили определяется по формулам, аналогичным формуле для расчета медианы. Так значение первой квартили (Q1) определяется по формуле:
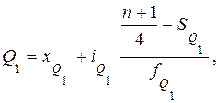 (4.19)
(4.19)
где  – нижняя граница интервала, в котором находится первая квартиль;
– нижняя граница интервала, в котором находится первая квартиль; 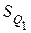 – накопленные итоги численностей интервалов, предшествующих интервалу, в котором находится первая квартиль;
– накопленные итоги численностей интервалов, предшествующих интервалу, в котором находится первая квартиль; 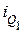 – величина первого квартильного интервала;
– величина первого квартильного интервала; 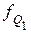 – частота интервала, в котором находится первая квартиль.
– частота интервала, в котором находится первая квартиль.
Вычислим значение первой квартили по данным табл. 4.3.:
 мин.
мин.
Таким образом 25% изделий произведены с затратами времени 12, 2 мин. и меньше на одну деталь, а 75% – больше чем 12, 2 мин.
Вторая квартиль  равна значению медианы, т.е.
равна значению медианы, т.е.
Q2=Me. (4.20)
Значение третьей квартили  определяется по формуле:
определяется по формуле:
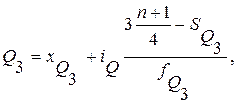 (4.21)
(4.21)
(условные обозначения те же, что и для величины Q1, только применительно к расчету третьей квартили). Определим значение третьей квартили на основе данных табл. 4.3.:
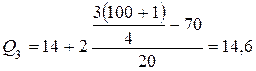 мин.
мин.
Применительно к данному примеру следует, что 75% изделий произведены с затратами времени 14, 6 мин. и меньше на одну деталь, а 25% – больше, чем 14, 6 мин.
ЗАДАЧИ
Задача 4.1. Выполнение задания по выпуску продукции каждым из трех заводов характеризуется следующими данными: по первому заводу – 110%, по второму – 96%, по третьему – 115%. Определите средний процент выполнения задания по выпуску продукции по трем заводам вместе, если известно, что по каждому заводу было установлено одинаковое задание по выпуску продукции. Дайте обоснование выбора формулы расчета средней.
Задача 4.2. Выполнение сменных норм выработки в трех бригадах рабочих сдельщиков характеризуется следующими данными: первая бригада – 112%; вторая бригада – 108%; третья бригада – 110%. Вычислите средний процент выполнения сменных норм выработки, если известно, что фактический объем выполненной работы в каждой из бригад одинаков. Какую формулу средней здесь следует применить? Покажите преобразовательные процедуры обоснования формулы расчета среднего процента выполнения норм выработки.
Задача 4.3. Четверо рабочих в течение рабочей смены (8 часов) были заняты изготовлением деталей одного и того же наименования. Каждый из рабочих на изготовление одной детали затрачивал: первый – 5 мин., второй – 8 мин., третий – 10 мин., четвертый – 6 мин. Определите средний уровень затрат времени на изготовление одной детали всеми рабочими.
Задача 4.4. Имеются следующие данные о распределении рабочих механического цеха завода по уровню квалификации (тарифному разряду):
| Тарифный разряд рабочих | ||||||
| Число рабочих в процентах к итогу |
Вычислите средний тарифный разряд рабочих цеха.
Задача 4.5. Если в средней арифметической взвешенной все варианты увеличить вдвое, а частоты соответственно уменьшить вдвое, то каким образом изменится среднее значение признака. Принятое решение сформулируйте доказательно, произведя соответствующие преобразования в формуле средней арифметической взвешенной.
Задача 4.6. Имеются следующие данные по трем машиностроительным заводам за первый и второй кварталы:
| Номер завода | I квартал | II квартал | ||
| План выпуска продукции, млн. р. | Процент выполнения плана | Фактический выпуск продукции, млн. р. | Процент выполнения плана | |
Определите средний процент выполнения плана выпуска продукции в каждом из кварталов и за первое полугодие по трем заводам вместе.
Задача 4.7. Имеются следующие данные по двум хозяйствам:
| Наименование зерновых культур | Хозяйство № 1 | Хозяйство № 2 | ||
| Посевная площадь, га | Урожайность, ц/га | Валовой сбор зерна, ц | Урожайность, ц/га | |
| Пшеница озимая | 42 000 | |||
| Пшеница яровая | 29 700 | |||
| Рожь | 47 500 | |||
| Ячмень | 56 000 |
Определите среднюю урожайность зерновых по каждому из хозяйств. По хозяйству №1 определите среднюю урожайность зерновых культур по данным о размере посевов и по удельным весам посевов отдельных видов культур в общем их итоге.
Задача 4.8. По трем отделениям механического цеха имеются следующие данные:
| Отделения цеха | Январь | Февраль | ||
| Число рабочих, чел. | Средняя месячная з/пл., тыс. ден. ед. | Фонд з/пл., тыс. ден. ед. | Средняя месячная з/пл., тыс. ден. ед. | |
| Токарное | 6, 5 | 7, 0 | ||
| Фрезерное | 5, 8 | 6, 2 | ||
| Шлифовальное | 7, 0 | 7, 5 |
Определите среднюю месячную заработную плату рабочих по цеху в целом в январе и феврале.
Задача 4.9. Имеются следующие данные по трем заводам, производящим силикатный кирпич:
| Номер завода | Базисный период | Отчетный период | ||
| Затраты на производство млн. р. | Себестоимость 1 тыс. кирпича, тыс. р. | Произведено кирпича, тыс. шт. | Себестоимость 1 тыс. кирпича, тыс. р. | |
| 11 000 | 11 500 |
Определите для каждого периода среднюю себестоимость 1 тыс. кирпича по трем заводам вместе как по абсолютным, так и по относительным (удельным) весам.
Задача 4.10. Определите среднюю урожайность зерновых культур и среднюю себестоимость 1 ц зерна на основе следующих данных:
| Номер хозяйств | Посевная площадь зерновых культур, га (П) | Урожайность зерновых культур, ц/га (У) | Себестоимость 1 ц зерна, тыс. р. (Z) |
Задача 4.11. Имеются следующие данные о производстве продукции, расходе сырья на единицу изделия и о его цене (продукция по всем трем предприятиям однородная):
| Номер предприятия | Произведено изделий, тыс. шт. (f) | Расход сырья на единицу изделия, кг (х) | Цена 1 кг сырья, тыс. р. (р) |
| 2, 5 | |||
| 2, 2 | |||
| 2, 0 |
Определите средний расход сырья на единицу изделия и среднюю цену 1 кг сырья, израсходованного на производство продукции.
Задача 4.12. Имеются следующие данные о распределении бревен по величине их радиуса:
| № штабеля бревен | ||||
| Радиус бревен, см | ||||
| Количество бревен в штабеле, шт. |
Определите средний квадрат радиуса и на его основе среднюю площадь бревен и общий объем кубатуры бревен в м3 (длинна бревен в каждом из штабелей 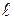 =10 м).
=10 м).
Задача 4.13. Известны следующие данные о средней месячной заработной плате работающих по четырем предприятиям машиностроения и фонде заработной платы каждого из предприятий в процентах к общему фонду заработной платы всех предприятий:
| Номер предприятия | Средняя месячная заработная плата, тыс. ден. ед. | Фонд заработной платы в процентах к итогу. |
| 5, 0 | ||
| 8, 0 | ||
| 6, 0 | ||
| 4, 0 |
Определите среднюю месячную заработную плату работающих по всем предприятиям вместе. Какой вид средней здесь следует применить? Что является весами при расчете средней месячной заработной платы?
Задача 4.14. На каждом из трех заводов зафиксированы следующие показатели процента бракованной продукции: на первом – 8 на втором – 10; на третьем – 5. Определите средний процент бракованной продукции по трем заводам вместе, если известно, что объем произведенной продукции по каждому из заводов в процентах к итогу составил соответственно 20, 30 и 50.
Задача 4.15. Определите средний процент бракованной продукции по трем заводам вместе, если известно, что на первом заводе процент брака составил 8, на втором – 5, на третьем – 6, а удельный вес бракованной продукции по каждому из заводов в процентах к итогу составил соответственной 20, 20 и 60.
Задача 4.16. Имеются следующие данные о проценте брака по четырем однотипным заводам при одинаковом объеме производства продукции: по первому – 6, по второму – 8, по третьему – 7 и четвертому – 8, 4. Определите средний процент брака по четырем заводам вместе.
Задача 4.17. Определите средний процент брака при одинаковом объеме бракованной продукции на каждом из трех заводов. Процент брака на первом заводе составил 5, на втором – 8, и на третьем – 10.
Задача 4.18. Имеются следующие данные по трем машиностроительным заводам:
| Номер завода | Базисный период | Отчетный период | ||
| Объем произведенной продукции, млн. руб. | Процент стандартной продукции | Объем стандартной продукции, млн. руб. | Процент стандартной продукции | |
Определите средний процент стандартной продукции по трем заводам вместе отдельно в базисном и отчетных периодах.
Задача 4.19. Три автомобильных завода работают в одинаковом сменном режиме времени. Определите средний интервал времени выпуска автомобилей, если известно, что на первом заводе каждый автомобиль выпускается через каждые 20 мин., на втором – через 25 мин., а на третьем – через 40 мин. Обозначьте исходную формулу расчете средней применительно к данному примеру.
Задача 4.20. Имеются следующие данные о распределении рабочих завода по уровню месячной заработной платы:
| Группа рабочих по уровню месячной з/пл., тыс. ден. ед. | До 3 | 3-5 | 5-7 | 7-9 | 9 и более |
| Число рабочих |
Определите:
1) средний уровень месячной заработной платы рабочих: а) обычным способом; б) с использованием первого условного момента.
2) значение моды, медианы и квартильных характеристик (первой, второй и третьей). Поясните полученные результаты.
Задача 4.21. Распределение рабочих механического завода по длительности производственного стажа характеризуются следующими данным:
| Группы рабочих по стажу работы, лет. | до 4 | 4-8 | 8-12 | 12-16 | 16-20 | 20 и более |
| Число рабочих в процентах к итогу |
Определите те же статистические характеристики, что и в задаче 4.20.
Задача 4.22. Имеются следующие данные о группировке промышленных предприятий города по стоимости основных фондов:
| Группы заводов по стоимости основных фондов, млрд. р. | до 10 | 10-14 | 14-18 | 18-22 | 22-26 | 26 и более |
| Число предприятий в процентах к итогу |
Определите те же статистические характеристики, что и в задаче 4.20.
Задача 4.23. Имеются следующие данные о распределении коров по дневному надою молока:
| Группы коров по дневному надою молока, кг | до 10 | 10-14 | 14-18 | 18-22 | 22 и более |
| Число коров |
Определите те же статистические характеристики, что и в задаче 4.20.
Задача 4.24. Распределение рабочих по общему стажу работы и квалификации характеризуется следующими данными:
| Группы рабочих по стажу работы, лет | Группы рабочих по тарифному разряду | Итого | ||||
| До 5 | ||||||
| 5-10 | ||||||
| 10-25 | – | |||||
| Итого |
Определите: 1) средний тарифный разряд рабочего каждой группы по стажу работы;
2) средний тарифный разряд всех рабочих: а) непосредственно на основе данных условия задачи; б) по вычисленным о среднем тарифном разряде по каждой из трех выделенных по стажу работы групп рабочих.
3) средний стаж рабочего каждой группы по уровню квалификации;
4) средний стаж всех рабочих: а) непосредственно по данным условия задачи; б) по вычисленным показателям среднего стажа работы рабочих данной квалификации.
Можно ли при вычислении этих средних показателей пользоваться формулой простой арифметической?
Задача 4.25. При каких условиях возможно вместо средней арифметической взвешенной использовать расчет средней по формуле простой арифметической, а также вместо средней гармонической взвешенной представляется возможным использовать формулу средней гармонической простой?
Задача 4.26. Имеются следующие данные по трем предприятиям, вырабатывающим однородную продукцию.
| Предприятие | 2005 г. | 2006 г. | ||
| Затраты времени на единицу продукции, чел.ч. | Выпущено продукции, тыс. ед. | Затраты времени на единицу продукции. чел.ч. | Затраты времени на всю продукцию, чел.ч. | |
| 0, 36 | 50, 1 | 0, 34 | 19 975 | |
| 0, 48 | 48, 1 | 0, 48 | 22 248 | |
| 0, 53 | 28, 8 | 0, 53 | 13 462 |
Обоснуйте выбор формул средних и по этим формулам определите для каждого года средние затраты времени на продукцию по трем предприятиям вместе. Сравните полученные результаты и сформулируйте выводы,
Задача 4.27. Имеются данные по трем предприятиям, выпускающим одинаковые изделия:
| Предприятие | Фактический выпуск продукции, млн р. | % выполнения планового задания | % продукции высшего сорта |
| 1002, 3 | 102, 8 | 82, 4 | |
| 907, 3 | 105, 5 | 94, 5 | |
| 674, 1 | 96, 3 | 89, 2 |
На основании приведенных данных по трем предприятиям, используя формулы соответствующих средних величин определите:
1) средний процент выполнения планового задания выпуска продукции;
2) средний процент продукции высшего сорта.
Задача 4.28. Имеются следующие данные о выпуске продукции по двум цехам трикотажной фабрики.
| Цех | I кв. | II кв. | ||
| Выпуск бракованной продукции, млн р. | Брак, % | Фактический выпуск продукции, млн р. | Брак, % | |
| 47, 50 | 0, 95 | 1, 035 | ||
| 39, 78 | 1, 02 | 1, 000 |
Вычислите процент брака в среднем по фабрике за I и II кварталы и за полугодие в целом.
Укажите, в каком квартале средний процент брака был ниже и какой вид средней нужно применять для вычисления каждого из этих показателей.
Задача 4.29. Имеются следующие данные по двум заводам, вырабатывающим однородную продукцию.
| Завод | 2005 г. | 2006 г. | ||
| Затраты времени на единицу продукции, чел- час. | Изготовлено продукции, шт. | Затраты времени на единицу продукции, чел- час. | Затраты времени на всю продукцию, чел- час. | |
| 3, 0 | 2, 8 | 459, 2 | ||
| 3, 6 | 3, 5 | 542, 5 |
Вычислите средние затраты времени на изготовление единицы продукции по двум заводам в 2005 и 2006 гг. Укажите, какие виды средних надо применить для вычисления этих показателей.
Задача 4.30. Имеются следующие данные о численности ткачих и их выработке за смену по цехам фабрики.
| Цех | Сентябрь | Октябрь | ||
| Средняя выработка ткани за смену на одну ткачиху, кв. м | Численность ткачих, чел. | Средняя выработка ткани за смену на одну ткачиху, кв. м | Выработано ткани за смену, кв. м | |
| 12 160 | ||||
Вычислите среднюю выработку ткани на одну ткачиху в среднем по фабрике за:
1) сентябрь;
2) октябрь.
Укажите, какой вид средней величины нужно применить для исчисления этих показателей.
Задача 4.31. Имеются следующие данные по предприятиям, выпускающим одноименную продукцию
| Предприятие | 2005 г. | 2006 г. | ||
| Себестоимость единицы изделия, млн р. | Количество изделий, тыс. шт. | Себестоимость единицы изделия, млн р. | Затраты на продукцию, млрд р. | |
| 1, 0 | 1, 0 | |||
| 1, 2 | 1, 1 | |||
| 0, 9 | 0, 8 |
Вычислите среднюю себестоимость единицы изделия по трем предприятиям вместе:
а) за 2005 г.
б) за 2006 г.
Укажите, какие виды средних применялись. Сделайте вывод, на сколько процентов изменилась средняя себестоимость единицы изделия.
Задача 4.32. Имеются следующие данные о выработке одноименных деталей за смену рабочими трех цехов завода:
| Цех | Январь | Февраль | ||
| Средняя выработка деталей за смену одним рабочим, шт. | Число рабочих, чел. | Средняя выработка деталей за смену одним рабочим, шт. | Выработано деталей за смену всеми рабочими, шт. | |
Вычислите среднюю выработку деталей за смену одним рабочим по трем цехам вместе:
а) за январь;
б) за февраль.
Укажите, какие виды средних применялись. Сформулируйте выводы.
Задача 4.33. Имеются данные по двум бригадам о расходе сырья на производство однородной продукции
| Бригада | I кв. | II кв. | |||
| Расход сырья на тонну готовой продукции | Количество израсходованного сырья, т | Расход сырья на тонну готовой продукции | Изготовлено всего продукции, т | ||
| 0, 75 | 0, 8 | ||||
| 0, 66 | 0, 7 |
Вычислите средний расход сырья на тонну готовой продукции по двум бригадам в I кв. и во II кварталах. Укажите, какие виды средних надо применить для вычисления этих показателей и на сколько процентов средний расход сырья на тонну готовой продукции снизился во II кв. по сравнению с первым.
Задача 4.34. При выборочном обследовании 19-ти % изделий партии готовой продукции по методу бесповторного отбора получены следующие данные о содержании влаги в образцах:
| Влажность, % | Число образцов |
| до 13 | |
| 13-15 | |
| 15-17 | |
| 17-19 | |
| 19 и выше | |
| Итого: |
На основании данных выборочного обследования вычислите:
1) средний процент влажности готовой продукции;
2) моду и медиану влажности продукции.
Сделайте выводы.
Задача 4.35. В целях изучения стажа рабочих завода проведена 36%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
| Стаж, число лет | Число рабочих, чел. |
| до 5 | |
| 5-10 | |
| 10-15 | |
| 15-20 | |
| 20-25 | |
| 25 и выше | |
| И т о г о: |
На основе этих данных вычислите:
1) средний стаж рабочих завода;
2) моду и медиану стажа рабочих.
Сделайте выводы.
Задача 4.36. В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена 19%-ная механическая выборка, в результате которой получено следующее распределение изделий по массе:
| Масса изделия, г | Число изделий, шт. |
| до 40 | |
| 40-42 | |
| 42-44 | |
| 44-46 | |
| 46 и выше | |
| И т о г о: |
На основе этих данных вычислите:
1) среднюю массу изделия;
2) моду и медиану массы изделий.
Сделайте выводы.
Задача 4.37. В целях изучения дневной выработки рабочими завода проведена 20%-ная случайная бесповторная выборка, в результате которой получено следующее распределение рабочих:
| Группы рабочих с дневной выработкой изделий, шт. | Число рабочих, чел. |
| до 30 | |
| 30-34 | |
| 34-38 | |
| 38-42 | |
| 42-46 | |
| 46 и выше | |
| И т о г о: |
На основе этих данных вычислите:
1) среднедневную выработку изделий;
2) моду и медиану дневной выработки.
Сделайте выводы.
Задача 4.38. В целях изучения затрат времени на изготовление одной детали рабочими завода проведена 19%- ная случайная бесповторная выборка, в результате которой получено следующее распределение деталей по затратам времени:
| Затраты времени на одну деталь, мин. | Число деталей, шт. |
| до 20 | |
| 20-22 | |
| 22-24 | |
| 24-26 | |
| 26 и более | |
| И т о г о: |
На основе этих данных вычислите:
1) средние затраты времени на изготовление одной детали;
2) моду и медиану затрат времени.
Сделайте выводы.
Задача 4.39. В целях изучения урожайности озимой пшеницы в колхозах области проведено 19%- ное выборочное обследование 100 га посевов, отобранных в случайном порядке, в результате которого получены следующие данные (выборка бесповторная):
| Урожайность, ц с одного га | Посевная площадь, га |
| до 20 | |
| 20-24 | |
| 24-28 | |
| 28-32 | |
| 32 и выше | |
| И т о г о: |
На основе этих данных вычислите:
1) среднюю урожайность озимой пшеницы с одного га;
2) моду и медиану урожайности озимой пшеницы.
Сделайте выводы.
Задача 4.40. В целях изучения степени выполнения норм выработки на машиностроительном заводе было проведено 10%-ное выборочное обследование рабочих-сдельщиков, в результате которого получены следующие данные (отбор механический):
| Выполнение норм выработки, % | Число рабочих |
| до 100 | |
| 100-110 | |
| 110-120 | |
| 120-130 | |
| 130-140 | |
| 140 и более | |
| И т о г о: |
На основе этих данных вычислите:
1) средний процент выполнения норм выработки одним рабочим- сдельщиком;
2) моду и медиану выполнения норм выработки.
Сделайте выводы.
Задача 4.41. В целях изучения уровня рентабельности предприятий отрасли проведена 36%-ная механическая выборка, в результате которой получены следующие данные об уровне рентабельности:
| Уровень рентабельности, % | Число предприятий, % к итогу |
| До 15 | |
| 15-20 | |
| 20-25 | |
| 25-30 | |
| 30-35 | |
| 35-40 | |
| 40 и выше | |
| И т о г о |
На основе этих данных вычислите:
1) средний уровень рентабельности;
2) моду и медиану уровня рентабельности.
Сделайте выводы.
Ответы:
4.1. 107%. 4.2. 110%. 4.3. 6, 76 мин. 4.4. 4, 5 разряда. 4.5. Средняя увеличится вдвое. 4.6. 106, 2%; 108, 1%. 4.7. 28, 1 ц/га; 29, 2 ц/га. 4.8. 6, 5 тыс. ден. ед; 7 тыс. ден. ед. 4.9. 142 тыс. р.; 228, 8 тыс. р. 4.10. 28, 1 ц/га; 723, 13 тыс. р. 4.11. 2, 15 кг; 66, 05 тыс. р. 4.12. 343, 75; 1080 см2. 4.13. 4, 88 тыс. д.е. 4.14. 7, 1%. 4.15. 6, 06%. 4.16. 7, 35%. 4.17. 7, 06. 4.18. 85, 1%; 92, 7%. 4.19. 26, 1 мин. 4.20. 1) 6 тыс. д.е. 2) 6 тыс. д.е., 4, 2 тыс. д.е.; 7 тыс. д.е. 4.21. 1) 12 лет; 2) 10, 67 лет; 11, 5 лет; 9 лет; 15, 2 лет. 4.22. 1) 18 млрд. р. 2) 16, 67 млрд. р.; 17, 5 млрд. р.; 15 млрд. р.; 21, 2 млрд. р. 4.23. 1) 15, 6 кг; 2) 15, 67 кг; 15, 6 кг; 13, 2 кг; 17, 6 кг. 4.24. 1) 3, 925 разряда; 4 разряд; 4, 875 разряда; общий средний тарифный разряд рабочих 4, 265; 3) 5, 357 лет; 6, 625 лет; 9, 5 лет; 11, 346 лет; 12, 794 лет; общий средний стаж рабочих 9, 7 лет. 4.25. средняя арифметическая взвешенная преобразуется в среднюю арифметическую простую.
|