
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые характеристики дискретной случайной величины
|
|
Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями.
I. Математическое ожидание M(X).
Математическим ожиданием M(X) случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности, т.е. 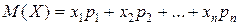 .
.
Смысл математического ожидания. Пусть произведено N независимых опытов, в каждом из которых X принимает определенное значение. Например,
x1 появилось m1 раз,
x2 появилось m2 раз,
...
xn появилось mn раз.
Ясно, что m1+ m2+…+ mn=N.
Вычислим среднее арифметическое найденных случайных величин:
 , но
, но
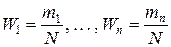 - относительные частоты, т.е.
- относительные частоты, т.е.
 .
.
Допустим, что число испытаний достаточно велико, значит
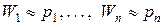 , т.е.
, т.е.
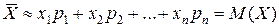 ,
,
Или
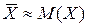 .
.
Значит математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Пример:
1)
| X | 3 | 5 | 2 |
| P | 0, 1 | 0, 6 | 0, 3 |

2)Найти математическое ожидание числа появлений события А в одном испытании, если вероятность появления события А равно р.
| X | 1 | 0 |
| P | р | q |
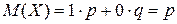 .
.
Прежде, чем рассматривать свойства математического ожидания, введем некоторые понятия.
Определение 1. С – постоянная дискретная случайная величина. Она принимает одно возможное значение С с вероятностью р=1.
| X | С |
| P | 1 |
Определение 2. СX –дискретная случайная величина, которая имеет вид и
Если
| X | x1 | x2 | x3 | … | xn |
| P | p1 | p2 | p3 | … | pn |
то
| СX | Сx1 | Сx2 | Сx3 | … | Сxn |
| P | p1 | p2 | p3 | … | pn |
Т.е. возможные значения случайной величины СХ равны Сxi, а вероятности равны соответствующим вероятностям случайной величины Х.
Определение 3. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.
Определение 4. Произведение независимых случайных величин Z=XY.
Если
| X | x1 | x2 |
| P | p1 | p2 |
| Y | y1 | y2 |
| P | g1 | g2 |
то
| XY | x1 y1 | x2 y1 | x1 y2 | x2 y2 | - возможные значения |
| P | p1 g1 | p2 g1 | p1 g2 | p2 g2 | - их вероятности |
Определение5. Суммой случайных величин X и Y Z=X+Y, называют случайную величину, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y. Вероятности возможных значений Z=X+Y для независимых величин X и Y равны произведениям вероятностей слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.
Если
| X | x1 | x2 |
| P | p1 | p2 |
| Y | y1 | y2 |
| P | g1 | g2 |
то
| X+Y | x1 +y1 | x2 +y1 | x1 +y2 | x2 +y2 | - возможные значения |
| P | p11 | p21 | p12 | p22 | - их вероятности |