
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Биноминальное распределение
|
|
Пусть производится n независимых испытаний, в каждом из которых событие A может появиться, либо не появиться. Вероятность наступления события во всех испытаниях постоянна равна p (вероятность не появления q=1-p). Пусть X – число появлений события A в этих испытаниях. Найдем закон распределения величины X:
| X | n | n-1 | … | k | … | 0 |
| P | pn | npn-1q | … | Cnkpkqn-k | … | qn |
Найдем мат.ожидание и дисперсию.
Очевидно, что общее число появлений события А складываетсяиз чисел появлений события в отдельных испытаниях, т.е.
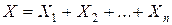
| X1 | 1 | 0 |
| P | p | q |
 , значит
, значит 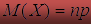 .
.
Аналогично, 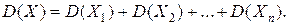
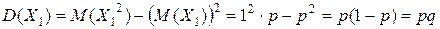 , т.е.
, т.е.  .
.
Пример: Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0, 6. Найти закон распределения, мат.ожидание и дисперсию случайной величины X – числа появления события в этих испытаниях.
Решение: n=10; p=0, 6; q=0, 4.
| X | 0 | 1 | … | 10 |
| P | 0, 4n | С101 0, 61 0, 49 | … | 0, 6n |

· Если же в задаче количество испытаний велико, то вместо формулы Бернулли используют асимптотическую формулу Лапласа
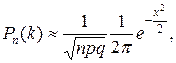 где
где 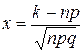 .
.
Причем, 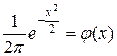 - имеются таблицы для этой функции.
- имеются таблицы для этой функции.
· Если же в задаче количество испытаний велико, а р – мало ( ), то используют асимптотическую формулу Пуассона
), то используют асимптотическую формулу Пуассона
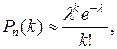 где
где  . Это закон распределения Пуассона.
. Это закон распределения Пуассона.
Пример:
Найти вероятность того, что событие A наступит ровно 80 раз в 400 испытаниях, если р=0, 2.
Решение:
n=400; k=80; p=0, 2; q=0, 8.
По формуле Лапласа 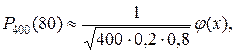

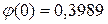 ,
,

По формуле Бернулли

Замечание: Если n=10; k=8; p=0, 75; q=0, 25, то
По формуле Лапласа 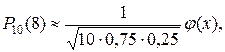
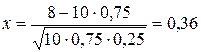 ,
,
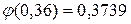 ,
,
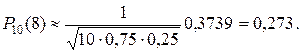
По формуле Бернулли
 .
.
Вывод: Так как n – мало, то расхождение большое.
Пример: Завод отправил на базу 5000 доброкачественных деталей. Вероятность того, что изделие в пути повредится 0, 0002. Найти вероятность того, что на базу придут 3 негодных изделия.
Решение: Если n=5000; k=3; p=0, 0002, то по формуле Пуассона
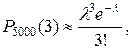 где
где  .
.
Значит, 