
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Энтропия и термодинамическая вероятность
|
|
Согласно выражению (4.32) энтропия замкнутой термодинамической системы в необратимых процессах возрастает, при этом максимальное значение энтропии достигается тогда, когда система приходит в состояние термодинамического равновесия.
Молекулярно-кинетическое истолкование такой формулировки второго начала термодинамики было дано Больцманом, который ввел в теорию теплоты статистические представления, основанные на том, что необратимость тепловых процессов имеет вероятностный характер.
Переход из неравновесного состояния в равновесное представляет собой переход системы из состояния, которое может осуществляться меньшим числом способов в состояние, осуществляемое большим числом способов. Наиболее вероятным для системы будет то состояние, которое осуществляется наибольшим числом способов (состояние термодинамического равновесия). Поэтому маловероятным был бы самопроизвольный выход системы из состояния термодинамического равновесия.
Число способов, которыми может быть осуществляется данное равновесное состояние, называется термодинамической вероятностью и обозначается 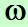 .
.
Число способов 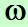 , которыми может осуществляется данное состояние системы, состоящее, например, из двух тел, равно произведению чисел способов
, которыми может осуществляется данное состояние системы, состоящее, например, из двух тел, равно произведению чисел способов 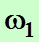 и
и 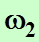 , которыми могут быть осуществлены состояния каждого из этих тел в отдельности:
, которыми могут быть осуществлены состояния каждого из этих тел в отдельности:
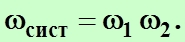 (4.33)
(4.33)
Больцман предложил существование функциональной зависимости между энтропией и термодинамической вероятностью. Для системы, состоящей из двух частей:
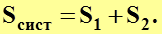 (4.34)
(4.34)
Таким образом,
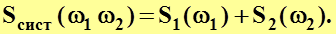 (9.35)
(9.35)
Такому функциональному уравнению удовлетворяет логарифмическая функция, поэтому
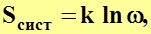 (4.36)
(4.36)
где 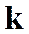 ─ постоянная Больцмана.
─ постоянная Больцмана.
Из этой формулы следует, что при возрастании вероятности состояния системы увеличивается и энтропия системы, значение которой при равновесии должно быть максимальным, как и значение 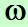 .
.
С принципом возрастания энтропии в системах связаны представления о тепловой смерти Вселенной, выдвинутые Клаузиусом. Однако, современные представления говорят, что Вселенную нельзя рассматривать как конечную замкнутую систему.